


Bertil Lindblad
(1962)
noticed that  -
-  /2 for angular
rotation rate
/2 for angular
rotation rate  and
epicyclic frequency
and
epicyclic frequency  was
about constant with radius in galaxy disks. He suggested that spirals are
fixed patterns with an angular rotation rate
was
about constant with radius in galaxy disks. He suggested that spirals are
fixed patterns with an angular rotation rate
 -
-
 /2, moving
through a disk of stars with a radial variation in the stellar rotation
rate
/2, moving
through a disk of stars with a radial variation in the stellar rotation
rate  . Thus stars
and gas move through the spiral pattern. This
was the beginning of spiral density wave theory, although it was not
quite right yet. Lindblad showed rotation curves for 3 galaxies,
. Thus stars
and gas move through the spiral pattern. This
was the beginning of spiral density wave theory, although it was not
quite right yet. Lindblad showed rotation curves for 3 galaxies,
 versus
versus
 , and
a nearly constant
, and
a nearly constant  -
-
 /2.
Rotation curves were difficult measurements at that time, and
derivatives in the rotation curves, as in the evaluation of
/2.
Rotation curves were difficult measurements at that time, and
derivatives in the rotation curves, as in the evaluation of
 , were highly inaccurate.
, were highly inaccurate.
The main problem with Lindblad's theory was that it had no forcing.
Also,  -
-
 /2 is not quite constant.
Lin & Shu (1964)
introduced a more dynamically correct spiral density wave theory. They
realized
that
/2 is not quite constant.
Lin & Shu (1964)
introduced a more dynamically correct spiral density wave theory. They
realized
that  -
-
 /2 could be forced by
the spiral's gravity to a
radial-constant value, even if it was not constant from the average
rotation curve. Then the stellar orbits could be closed for a wide
range of radii at a fixed pattern speed. The angular pattern speed
would be slightly different from
/2 could be forced by
the spiral's gravity to a
radial-constant value, even if it was not constant from the average
rotation curve. Then the stellar orbits could be closed for a wide
range of radii at a fixed pattern speed. The angular pattern speed
would be slightly different from
 -
-
 /2, and where it
equaled this value, there would be a resonant interaction between the
forcing from the spiral and the stellar epicyclic motions. This
resonance would absorb wave energy and put it into random stellar
motions, causing the wave to stop propagating at this place. This
position became known as the inner Lindblad resonance. Another
resonance position is where
/2, and where it
equaled this value, there would be a resonant interaction between the
forcing from the spiral and the stellar epicyclic motions. This
resonance would absorb wave energy and put it into random stellar
motions, causing the wave to stop propagating at this place. This
position became known as the inner Lindblad resonance. Another
resonance position is where
 +
+
 /2 equals the spiral pattern
speed. This is the outer Lindblad resonance. Other resonances at
/2 equals the spiral pattern
speed. This is the outer Lindblad resonance. Other resonances at
 -
-
 /3 and
/3 and
 +
+
 /3, occur as well,
limiting the range for three-arm spirals in this case. There are similar
limits for 4 arm spirals, etc., and finally the last resonance where
/3, occur as well,
limiting the range for three-arm spirals in this case. There are similar
limits for 4 arm spirals, etc., and finally the last resonance where
 itself equals the pattern speed. This is the corotation resonance,
where the same stars are always inside the wave crest, following it
around at the same angular speed.
itself equals the pattern speed. This is the corotation resonance,
where the same stars are always inside the wave crest, following it
around at the same angular speed.
The Lin-Shu mechanism works because just inside an arm, spiral gravity
pulls a star outward for short time, slowing it down a little as it
rises in its epicyclic path. Just outside an arm, spiral gravity pulls
the star inward, speeding it up as it falls inward in its epicyclic
motion. These slow-downs and speed-ups cause the ends points of each
epicycle to advance a little, closing the orbits in a rotating frame
with a rate
 p
such that
p
such that  -
-
 /2 <
/2 <
 p <
p <
 +
+
 /2. The gravitational
effect can be seen in the dispersion relation written by
Toomre (1969):
/2. The gravitational
effect can be seen in the dispersion relation written by
Toomre (1969):
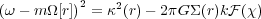 |
(2.1) |
where  is the rate of
change of the
spiral phase in a fixed coordinate system, equal to m times the
pattern speed, m is the number of symmetric spiral arms,
is the rate of
change of the
spiral phase in a fixed coordinate system, equal to m times the
pattern speed, m is the number of symmetric spiral arms,
 is
the mass column density in the disk, k is the wavenumber, and
is
the mass column density in the disk, k is the wavenumber, and
 is an integral over
stellar motions that depends on
is an integral over
stellar motions that depends on
 = k2
= k2
 u2 /
u2 /
 2 for rms
radial speed of the stars
2 for rms
radial speed of the stars
 u. Lindblad's
theory did not have the last term on the
right, which is from disk gravity. Traveling waves exist for Toomre
parameter Q > 1, i.e., for disks that are stable to radial
perturbations.
u. Lindblad's
theory did not have the last term on the
right, which is from disk gravity. Traveling waves exist for Toomre
parameter Q > 1, i.e., for disks that are stable to radial
perturbations.
Toomre (1969) noted that although the Lin-Shu dispersion relation for spiral waves has a phase velocity equal to the proposed pattern speed, it also has a group velocity which causes the wave crests to move inward, i.e., the spirals wrap up. Thus the "quasi-stationary" spiral density wave theory of Lin, Shu, Roberts, Yuan, and other collaborators at that time, did not work as they originally proposed. Toomre showed that for a flat rotation curve, disk-dominated gravity, and constant stability parameter Q, the Lin-Shu dispersion relation becomes relatively simple,
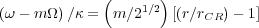 |
(2.2) |
for radius r and corotation radius rCR. In this
case, the time derivative of the dimensionless wavenumber increases at a
rate equal to half the rate of change in the phase,
 /2. When the wavenumber
increases with time, the spirals get closer together, which means they
migrate inward. This is a fast migration, almost as fast as purely
material arms would wrap up from shear.
/2. When the wavenumber
increases with time, the spirals get closer together, which means they
migrate inward. This is a fast migration, almost as fast as purely
material arms would wrap up from shear.
Toomre (1969)
proposed that spirals are not quasi-stationary, but
transient, provoked either by interactions
(Toomre & Toomre
1972)
or noise
(Toomre & Kalnajs
1991).
Kormendy &
Norman (1979)
noted that "grand design" spirals are
either in barred galaxies, in the rising parts of rotation curves
(where  -
-
 /2 ~ 0) or in
interacting galaxies. This would be consistent with Toomre's picture.
Toomre (1981)
identified the cause of transient spirals as "swing amplified
instabilities." Many groups have studied these instabilities numerically
(e.g.
Fuchs et
al. 2005).
/2 ~ 0) or in
interacting galaxies. This would be consistent with Toomre's picture.
Toomre (1981)
identified the cause of transient spirals as "swing amplified
instabilities." Many groups have studied these instabilities numerically
(e.g.
Fuchs et
al. 2005).
The quest for a theory of quasi-stationary spiral structure was not over, though. Mark (1974), Lau et al. (1976), and Bertin et al. (1989) proposed a "modal theory" in which inward-moving waves reflect or refract off of a bulge or bar and come back out as leading (WASER2; reflection) or trailing (WASER1; refraction) spiral arms. When they reach the corotation resonance moving outward, they amplify. Part of the wave then turns around to come back in and another part of the wave keeps going outward. The result is a standing wave pattern, amplified from initial disk noise at corotation and forming a long-lived grand-design spiral. The corotation radius is where the outward-moving wave meets the inward-moving wave on the opposite side of the galaxy for a two-arm spiral. If the outward moving wave is leading, then at the meeting place, the swing amplifier can transform this leading wave into a strong trailing wave. For example, an inward moving wave starting at corotation in one arm of a two-arm spiral can reflect off of a bulge and move back out as a leading wave until it meets the other arm at the same radius where it started. It amplifies as it is converted into a trailing arm, adds to the original trailing arm, and then a stronger trailing arm comes in again. Trailing waves that start at different radii will not reflect and meet the opposite arm at the same radius, and so will not add to the original wave after amplification. Thus, out of all the disk noise and small spirals that they initiate, only the spiral with the ability to amplify reflected or refracted waves and reinforce itself will grow. This defines the corotation radius. Bertin et al. (1989) described this process in detail.
Spiral wave modes could exhibit an interference pattern between the inward and outward moving waves. Interference acts to modulate the amplitudes of the main arms or it may introduce slight phase shifts in the main arms. Such modulation is present in the model solutions shown by Bertin et al. (1989). Elmegreen et al. (1992) reported such interference patterns, but a more modern analysis is needed.
The various theories of spiral wave formation may be reduced to four basic types: random and localized swing-amplified spirals that are primarily in the gas (because the stellar disk is somewhat stable); random and localized swing-amplified spirals that are in the stars and the gas together; transient global waves that are in the stars and gas, and standing wavemodes that are in the stars and gas. The first type produces flocculent spiral arms and a smooth underlying stellar disk (e.g., NGC 5055), the second type produces multiple stellar and gaseous arms (e.g., NGC 3184), the third type produces long spiral arms in the stars and gas (e.g., NGC 628), and the fourth type produces strong two-arm spirals in the stars and gas, usually in response to some global perturbation like a galaxy interaction (e.g., M51, M81). Aside from M81, these galaxy examples were chosen from the THINGS survey (Walter et al. 2008).
A spiral wavemode may be compared to the pure-tone ringing of a bell after some multi-frequency impact disturbs it (e.g., it is hit by a hammer or bowed by a violin string). Random swing-amplified spirals have been called spiral chaos. They are the primary response to gravitational instabilities in the stars and gas and therefore have a strong connection with star formation and the origin of interstellar turbulence in the absence of global wavemodes (e.g., Thomasson et al. 1992, Bournaud et al. 2010). Global spiral waves or wavemodes also have a connection with star formation because of the way they force the gas into a dense molecular phase in the dust lanes (which are shock fronts) and organize it to follow the underlying stellar spiral.