Clusters are the most massive bound and quasi-relaxed objects in the
Universe. They have total masses of 1014 to above
1015
M
. The
total gas fraction is about 16 per cent with about
13 per cent in the hot ICM and the remaining 3 per cent in stars in
the cluster galaxies. The remaining 84 per cent of the mass is in dark
matter. Gas densities in cluster centers range from as much as
10-1 cm-3 in peaked clusters to 10-3
cm-3 in the
non-peaked ones. This is in stark contrast to the mean cosmic density
of baryons of about 10-8 cm-3.
 |
 |
Figure 1. Chandra X-ray (left) and DSS optical (right) image of the relaxed massive galaxy cluster, Abell 2029. Both images are 4 arcminutes on a side. Abell 2029 is an extremely regular and putative cooling flow cluster. The X-ray image demonstrates how the intracluster medium pervades the space between the galaxies shown in the optical image. Figure adapted from http://www.chandra.harvard.edu/ (X-ray: NASA/CXC/UCI/A.Lewis et al. Optical: Pal.Obs. DSS). |
|
The characteristic or virial radius, Rv, of a cluster,
defined from the theory of structure collapse in an expanding universe as
where the mean density of the cluster is 200 times the critical
density of the Universe (i.e. 200 × 3H2 /
8
G, with the Hubble
constant at redshift z varying as H /
H0 =
[
m(1 +
z)3 + 1
- m]1/2, is typically between 1 and 3
Mpc. The gas is
heated by gravitational infall to temperatures close to the virial
temperature kT ~ GMmp /
Rv, which ranges in clusters
from 1-15 keV. The total X-ray luminosities range from about
1043 erg s-1 to 1046 erg
s-1. Objects at lower masses and
luminosities are groups which have from a few to tens of member
galaxies as compared with the hundreds of galaxies in a typical cluster.
Structure formation in the Universe proceeds in a hierarchical manner with the most massive objects, clusters, forming last, which means now. They continue to evolve by the infall of subclusters. The time since the last major merger is typically about 5 Gyr. About 20 per cent of clusters have had a more recent merger or are undergoing one. These are not the subject of this review.
Analytic and numerical simulations of cluster formation indicate that
the total X-ray luminosity LX
T2
in the absence of gas cooling and heating. This follows since
the X-ray luminosity is dominated by thermal bremsstrahlung so
LX
n2 T1/2
Rv3, the mean gas density n
M / Rv3 is constant and T =
M / Rv. The
temperature drops monotonically outward (by a factor of up to about
2). Observations instead show LX
T3
over the temperature range 2-8 keV with a wide dispersion at lower
temperatures and a possible flattening above. The simplest explanation
for this result is that the gas has had additional heating of 2-3 keV
per particle
(Wu et al. 2000,
Voit et al. 2003).
The effect of such heating is not to increase the temperature by that
amount but mostly to expand the gas (reducing its density and thus X-ray
luminosity). Such energy is plausibly due to energy output from
active galaxies, i.e. accreting black holes in cluster galaxies.
Alternatively, radiative cooling by removing the low-entropy gas in star
formation may reproduce the relation as well
(Voit & Bryan
2001).
The gas has generally been enriched to 0.3 of the Solar value by early supernovae. In relaxed clusters the potential and gas peak on the BCG. The metallicity often rises to solar or even higher around the BCG, probably due to SN Ia.
In relaxed, X-ray peaked, clusters the temperature profile is often
inverted in the inner core (i.e. R < 100 kpc) dropping inward as
T
r
with
~ 0.3-0.5. The gas
density there rises as n
r-1.
The overall profiles of the gas density and temperature depend on the entropy of the gas and thus on its heating and cooling history, subject to the equation of hydrostatic equilibrium,
 |
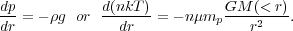(1) |
where p is the pressure,
is the mass
density, n is the number
density, k is Boltzmann's constant, T is the temperature,
G is Newton's constant, g is the gravitational
acceleration, M(< r) is the enclosed mass
within a radius r, mp is the proton mass, and
µ mp is the mean mass per particle. This
equation is used to estimate the total mass profile of clusters. Massive
ones can act as gravitational lenses for background galaxies as seen in
the optical band which provides another means to measure mass
profiles. Agreement between profiles determined by both methods
(Allen et
al. 2001c)
show that hydrostatic equilibrium
holds well in the main body of relaxed massive lensing clusters and
that any non-thermal pressure there is not dominant.