In the following sections we summarise the work of several groups, who have published in some cases several papers over the last decade. For brevity we have cited the more recent publications, whilst including material from earlier papers. Please refer to the cited papers for the full list of citations.
Korpi et al. (1999) constructed a comprehensive 3D model of a section of the galactic disc using parameters typical of the solar neighbourhood. The simulation included non-ideal MHD applied to a Cartesian grid of 0.5 × 0.5 × 2 kpc3. The resolution was about 83 parsecs3 (pc).
A vertical gravitational field (Kuijken and Gilmore 1989) and a shearing box to replicate the differential rotation were added. Thus a vertically stratified density profile for the interstellar medium (ISM) was applied. Heating was applied via Supernovae (SNe) Type I and II distributed randomly in time and space. Thermal conductivity, kinetic and magnetic viscosities were modelled and hyper viscosity applied to handle shocks.
The model replicated a multi-phase medium with the warm and hot phases in dynamic pressure equilibrium. The cold phase was not well reproduced through lack of a thermally unstable cooling function and low resolution.
The resultant ISM structure was highly differentiated in Z. Volume filling factors for temperature varied with height. Correlations for mass and velocity varied with temperature. The outward flow of the galactic fountain appeared to be described within the model, but the size of the model was insufficient to recover the global fountain behaviour.
In this study the warm phase was characterized by strong turbulent flow, but in the hot phase flows were on the scale of the remnant size enclosing the hot regions. This could be a feature of the numerical limits of the model.
With this model the group also studied the evolution of super-bubbles (SBs) of SNe clusters and how this was affected by the strength of the magnetic field and turbulence. They found that the frequency of SB break outs from the disc to the halo was significantly increased in a turbulent regime compared to previous experiments in a homogeneous medium.
The role of magnetic field strength in confining the bubbles was reduced. This could be arise from the increased random element to the field due to turbulence. Thus our expectation of the mixing between the disc and the halo would be higher.
Using a model since 2000 de Avillez and Breitschwerdt (2007) applied 3-D HD equations to a Cartesian grid 1 kpc2 by 8 kpc. They used adaptive mesh refinement (AMR) with a resolution ranging between 1.253 and 103 pc3. Also included was a vertical gravitational field and Type Ib+ Ic and Type II SNe. 60% were clustered in OB associations. Thermal conductivity and kinetic viscosity were neglected, but a thermally stable radiative cooling function was included.
The model evolved from hydrostatic equilibrium over a period of about
65 Myr to a dynamically steady state. Distinct cold (T
103K),
warm (103 < T
104K), warm
ionized (104 < T
105K) and
hot (T > 105K) phases were co-existing with varying
scale heights.
The cold phase was restricted to thin irregular strips around the mid-plane.
Hot gas dominated above 1.5 kpc and warm gas in the disc below 500 pc.
The model was extended vertically to ± 10 kpc between 2001 and 2007. They identified bubbles and super-bubbles typically up to 120 pc across and 200 pc high breaking out of the disc periodically. The cold sheet like structures that evolved, and which resembled the fragments of SN remnants, were in fact found not necessarily to be correlated with the bubble remnants, but in fact appeared to be a more general effect of the turbulent compressions and convection currents.
For a further adaption of the model to MHD an initial uniform 5.8 µG magnetic field in the azimuthal direction was included. The horizontal magnetized disc only briefly delayed the disc-halo cycle observed in the HD simulations and a hot phase volume filling factor of between 17 to 21% resulted both with HD and MHD.
Supersonic and super-Alfvénic flows led to strong MHD shocks.
A highly turbulent field evolved with a field strength ranging between
0.1 and 10 µG, which was not strongly correlated to the density
fluctuations. This is illustrated in figure 1.
Magnetic
pressure dominated the coldest gas, ram pressure dominant above 200 K and
thermal pressure above 105.5 K. In cold regions the relation
B 
did not hold, with
in the range -0.006
to 0.085.
 |
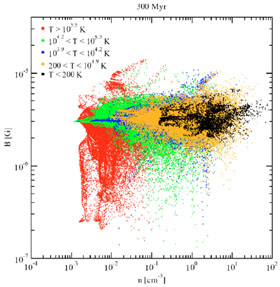Figure 1.
de Avillez and
Breitschwerdt (2007)
Scatter plot from study (2005) of B versus
|
Balsara et al. (2004) applied 3D ideal MHD to a (200 pc)3 region with SN randomly distributed. They included cooling (Raymond et al. 1976) and a constant diffuse heating term. Initial equilibrium was achieved by balancing heating and cooling for some given isothermal uniform density. The cooling considered could reproduce hot and warm phases, but not the cold phase.
They explored the results when varying the initial temperature and density and applying SN rates 1 and 100 × the rate in the solar neighbourhood. They investigated resolution at about 1.53 and 0.753 pc3. Stratification and differential rotation were not considered nor thermal conductivity and kinetic viscosity.
They found evidence of a fast dynamo sensitive to the SN rate. Over a 40 Myr simulation the field was amplified by two orders of magnitude. The growth rate was stronger in the high resolution, due to additional amplification available at smaller scales.
Taking a turbulent scale from an SN remnant to be 30pc they compared energy growth at scales above and below this. They found that eventually the growth rates were independent of scale.
Growth rates however were sensitive to SN rates, increasing up to a threshold where the magnetic energy was quenched. The growth of the field depended on the generation of helicity from the SN shocks interacting with the warm ISM. This was suppressed as the ISM became saturated by hot remnants. This effect had a critical rate somewhere between 12 and 40 times the galactic rate. There was also some increased amplification if the SN rate was more intermittent and field growth was most vigorous where the ISM had lower temperature and higher density.
Form 2002 Hanasz et al. (2009) investigated dynamo action with rigid rotation on a magnetized galactic disc. A uniform azimuthal field was applied to a rotating Cartesian domain 600 × 1800 × 600 pc with resolution 5 × 20 × 2.5 pc. They solved isothermal resistive MHD equations (neglecting kinetic viscosity).
In 2004 they included cosmic rays (CR) randomly injected at spherical locations representing SN remnants. Differential rotation was now included in a 0.5 × 1 × 1.2 kpc3 Cartesian grid, with a resolution of 103 pc3. The gravitational potential was as described by Ferrière (2001) and the cosmic ray diffusion tensor that of Ryu et al. (2003).
They observed an exponential growth in the magnetic field over a period of about 1000 Myr. Growth in the vertical component dominated, indicating that the CR buoyancy was important to the dynamics. Growth in the azimuthal direction reached 1400 × the seed field amplitude and 400 × in the radial direction.
Growth in the ideal regime onset rapidly after 250 Myr, due to magnetorotational instability (MRI). They argued that MRI amplification is suppressed when comparing the resistive MHD to ideal MHD due to magnetic reconnection in the thin current sheets generated by compressions in the field.
They observed that the fastest growing dynamo model resulted from periodic switching on and off the SN activity. Increased SN activity enhanced vertical field lines, increasing the loss of CR to the halo. Reduced activity supported their horizontal realignment thus enabling the amplitude of the field to grow. So the irregularity of the SN distribution can add to the dynamo.
Hanasz et al. (2009) investigated the source of the galactic magnetic seed field using their CR-driven dynamo model. Their domain was 502 × 10 kpc3 with resolution 1003 pc3. They started with an isothermal, vertically and radially stratified density, with a gravity potential and rotational shear, neglecting the central bulge.
Into an unmagnetized ISM they randomly exploded SN remnants. Some 10% of these included a randomly oriented weak dipolar magnetic field and CR equivalent to 10% of the typical kinetic energy of an SN remnant. Over a 4.8 Gyr simulation they produced a magnetic field, which became efficiently ordered within 2 Gyr, aligned along the spirals and including field reversals. The vertical field evolves an x-shaped configuration. In their movies, vertical outflows could be seen, which transported the counter polarity or helicity out of the system (Figure 2, small inserts). This seemed to be crucial for dynamo action.
 |
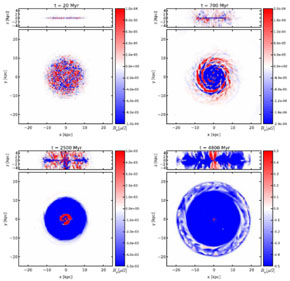Figure 2. Distribution of toroidal magnetic field from Hanasz et al. (2009). Unmagnetized regions are white, while positive and negative toroidal fields are shaded red and blue, respectively. Note that the color scale in magnetic field maps is saturated to enhance weaker magnetic field structures in the disc peripherals. The maximum magnetic field strengths are 5.9 × 10-4, 4.4 × 10-3, 1.5 and 29 µG at t = 0.02, 0.7, 2.5 and 4.8 Gyr respectively. |
The number and orientation of the spiral configurations is sensitive to the CR diffusion coefficients. They could not be derived from first principles without smaller scales, so the assumed value for diffusivity was large and unrealistic by necessity. Snap shots of the configuration are shown in Figure 2
In their 2002 2D model Slyz et al. (2005) investigated the characteristics of the spiral arms through isothermal HD. They used a 232 kpc2 with a resolution of 1152 pc2, including kinematic viscosity and applying a centrifugal and gravitational potential.
They varied the temperature, via the sound speed, the density profiles and rates of galactic rotation. Given the typical sound speed throughout the galaxy is far exceeded by the angular velocity of the gas relative to the spiral arms, it might not have been expected to have much effect the structure. They found that the non-axisymmetric pattern of the spiral galaxies diminished with increasing sound speed. At levels above 25 to 30 km s-1 they faded away. As sound speeds reduced the mass in the spiral arms increased.
They also found that the inner galaxy was more sensitive to changes in the fraction of galactic mass in the disc. As the disc fraction increased, velocities at the centre increased massively, whilst the structure in the outer regions was fairly insensitive to the disc fraction.
Subsequently Slyz et al. (2005) conducted a more localized analysis of star formation and SN feedback with a 3D hydrodynamical model. They used a 1.283 kpc3 Cartesian grid together with a particle mesh to track the stellar mass. The model included a thermally unstable cooling function and self-gravity. Stratification and any external gravity were not included.
A random Gaussian velocity perturbation was applied at the start onto an ISM of uniform density and temperature. They found that the regime saturated to a multi-phase medium, with velocity dispersion generally settling to levels consistent with the temperature of the medium: 15 km s-1, 30 and 75 for cold (< 2000 K), warm (< 105 K) and hot (<4 × 106 K) respectively. Velocities in the very hot (>4 × 106 K) are far more dispersed, with up to 500 km s-1 observed. These violent flows strip away elements of the cold dense star forming regions as they interact.
The distribution of mass was also a feature of the ISM temperature. The bulk of the volume was filled with hot diffuse medium of below 10-3 atoms cm3. The bulk of the mass was restricted to dense cold filamentary or sheet-like or worm-like structures accounting for a very small portion of the volume. In the absence of SN shocks the probability density functions (PDF) for the ISM were well described by the log normal. However with SN feedback a much higher incidence of increased density regions were observed, suggesting that star formation rates might be enhanced in a turbulent ISM.
Continuing the work from Balsara et al. (2004), Mac Low et al. (2005) studied the pressure distributions in the turbulent ISM with slightly differing results to those of Slyz et al. (2005). They applied ideal MHD equations in a (200 pc)3 domain, with 3.12, 1.56 and 0.83 parsec resolution, including a radiative cooling function and uniform uv-heating, but excluding gravity.
They randomly injected SN remnants, at 1 and 4 times the solar neighbourhood rate and analysed the evolution of the pressure distribution. They found the distribution of the pressure anomalies was independent of the orientation of the magnetic field due to the super-Alfvénic flows. Typically the hot gas formed discrete clumps, which were enclosed by warm or cold gas. The distribution of the colder dense clusters, tended not to be closely aligned directly to remnant structures. These formed on scales of dozens of parsecs and appeared to result from the general effects of large scale turbulence.
The presence of dense isolated filaments was more effective at breaking the momentum of remnants than equivalent mass more smoothly distributed and even with 4 times the SN rate hot zones remained unconnected and warm gas remained the largest volume filling factor. Even with SN driving they found the PDFs of the pressure were well described by the log normal and not a power law. The dispersion range was an order of magnitude away from the mean, far from equilibrium.
The turbulence in the galaxy is not adequately accounted for by SN activity alone so in 2005 Piontek and Ostriker (2007) modelled MRI-driven turbulence in the warm/cold phases of the ISM. They apply ideal MHD to a (200 pc)3 domain with resolution of 0.78 and 1.56 pc and realistic heating and cooling. They model differential rotation for the solar neighbourhood. The growth of turbulence was studied in a medium in uniform density and pressure and also one in which randomly distributed cold spherical clouds were included amongst the warm ISM. The MRI instability rapidly dominated and the saturated state was independent of the initial state. They studied the relationship between the MRI driven turbulence and the two-phase thermal structure derived from the cooling function by comparison to MRI is a single phase environment.
They found that the gas separated into two phases with peaks at 100 K and 8000 K, with an increasing spread of gas lying outside the equilibrium as turbulence saturated. The relative proportions of gas in the two phases was dependent on mean density, with the proportion of mass in the cold phase increasing substantially as the mean density increased.
Pressures were in reasonable equilibrium even in two phases without turbulence, but in the saturated state the pressure dispersion increased five fold.
Magnetic field growth 0.26 µG to about 2.5 µG was not sensitive to density nor phase. Away from SN activity MRI could certainly be a factor in the turbulent structure. Extrapolating their results for mean densities typical in the inner galaxy, R < 10, kpc they would predict turbulent velocity scales of about 4 km s-1, which could be a significant component.
Piontek and Ostriker (2007) included a vertical gravity profile, which now induced a vertical stratification in both density and temperature. The turbulent mixing of the warm ISM had a significantly higher scale height than the cold, which now was more clustered than in the earlier model. This combined with MRI to increase the magnetic pressure and they argued that the MRI could be responsible for suppressing star formation in the less dense outer region of the mid plane, even given the presence of cold clouds.
From 2006 Ryan Joung et al. (2009) conducted a HD study in a vertically stratified ISM including stellar and halo gravity and realistic diffuse heating and cooling plus SN turbulence. The vertical profile of the heating was realistically motivated. They neglected thermal conduction and kinetic viscosity, self-gravity and differential rotation.
They found the scale height of the galactic fountain to be several kpc. The volume filling factor near the mid-plane of the hot gas was inversely related to the magnitude of the diffuse heating, which they tested over a range up to 4 times that of Wolfire et al. (1995). This was due to a shift in the thermal equilibrium position to exclude the cold phase and increase the volume component of the warm gas.
The vertical density profile was out of agreement with observations which they attributed to lack of pressure, in the absence of magnetic and cosmic ray pressure.
In this study and also from 2009 they find that neither the density nor the kinetic energy wavelengths follow the Kolmogorov power law, but instead are far more widely dispersed.
Gressel et al. (2008) conducted a non-ideal 3D MHD simulation using the NIRVANA code. Their domain was 0.82 × 4 kpc3 and included realistic cooling, thermal conductivity and kinematic viscosity and rotational shear. A snapshot from their simulation is shown in figure 3 to illustrate the resolution and structure obtained through such simulations.
 |
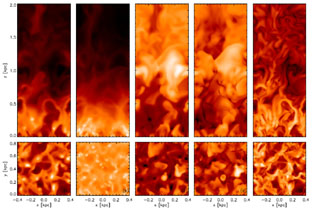Figure 3. Vertical slices from above the mid-plane (upper panels) and horizontal mid-plane slices (lower panels) after t = 112 Myr from Gressel et al. (2008). From left to right [in logarithmic scales]: number density[-4.82, 1.10]cm-3, column density [17.34, 21.55]cm-2, temperature[2.06, 7.20]K, velocity dispersion[-0.15, 2.77]km s-1 & magnetic field strength[-4.16, 0.34]µG. |
They tested a variety of SN rates (1/4 to 1 ×
0)
and rotational frequency (1 to 8 ×
0), where
0
and 0
denote the observed rates in the solar
neighbourhood, and measured the resulting dynamo parameters.
A result common to each run, was that the velocity dispersion increased with height up to about 1 kpc, even though the peak of SN activity was much lower. They found that turbulent pumping was directed inward, but balanced by a outward wind of comparable magnitude.
They found the dynamo not to be sensitive to the SN rates considered, 1, 2 & 4 × the observed rates. However the dynamo increased only with galaxy rotation rates 2 & 4 × the observed rate. They did not rule out however that these conclusions could also be sensitive to the assumed gravity and density profiles. They found no dynamo in the models without rotational shear.