4. VISIBLE MATTER AND DARK MATTER PARAMETER CORRELATIONS

Figure 6 illustrates our conclusion that, at M_V -18, the dwarf spiral, Im, and Sph galaxies in earlier figures form a sequence of decreasing baryon retention in smaller galaxies (KFCB; Kormendy & Bender 2012; Kormendy & Freeman 2014). In contrast, bulges and ellipticals together form a sequence of increasing dissipation during the formation of smaller galaxies. For M_V < -18 galaxies of all kinds, effective densities in stars are similar to DM densities at and interior to the same radius. For Sc-Im systems, this is by construction a consequence (1) of using maximum-disk decompositions and (2) of the "rotation curve conspiracy" (van Albada & Sancisi 1986), i.e., the observation that rotation curves of giant galaxies are roughly flat and featureless, so the parts of galaxies that are controlled by dark matter are not easily distinguished from the parts that are controlled by visible matter or even the parts that are controlled by different components in the visible matter (Figure 4). Caveat: for bulges and ellipticals, high baryon densities at r ≪ r_e may pull on DM halos enough to increase their central densities over the values for Sc-Im galaxies that are shown in Figure 6. But bulges and ellipticals have central projected densities that are more than 3 dex higher than the effective densities shown in Figure 6. So the central parts of early-type galaxies are very baryon-dominated. Even the central densities of disks are 0.7 dex (for an exponential) higher than the effective densities shown in Fig. 6. So even pure disks are moderately dominated by visible matter near their centers. Both results are qualitatively as expected: Visible matter needs to dissipate, sink inside the DM, and become self-gravitating enough to form stars and visible galaxies. And a great deal of dissipation happens in the wet mergers that make normal ellipticals (KFCB): their densities rise above DM densities by larger amounts at fainter M_V.

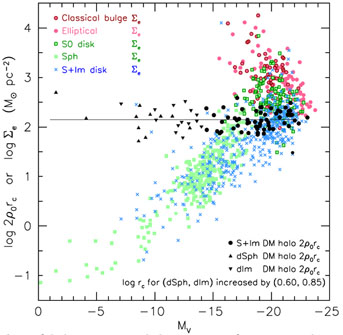Figure 6. Comparison of dark matter (DM) halo parameters from Kormendy & Freeman (2014) with visible matter parameters from Kormendy & Bender (2012). DM parameters are from maximum-disk rotation curve decompositions (black circles) or from cored isothermal halo models applied to the dispersion profiles of dSph galaxies (black triangles) or to the V ∝ r rotation curves and velocity dispersions of HI in dIm galaxies (upside-down black triangles) (see Kormendy & Freeman 2014, the source of this figure). Central projected densities are plotted for DM halos; effective surface densities Σe = Σ(re) are shown for visible components. Here re is the radius that contains half of the light of the component. Surface brightnesses are converted to stellar surface densities using mass-to-light ratios M / LV = 8 for ellipticals, 5 for classical bulges and S0 disks, and 2 for spiral galaxy disks, Im galaxies, and Sph galaxies.

The important point here is this: At M_V > -18, tinier dwarfs are more DM dominated, until by M_V -10, they are essentially dark galaxies with just enough of a frosting of stars so that they can be detected. I emphasize two important points: (1) The differences between dIm and dSph galaxies in all parameter correlations shown in this paper are small. Whether or not a galaxy retains cold gas and can still form stars in today's Universe is a second-order effect. This argues - as Dekel & Silk (1986) already emphasized - that the primary effect that engineers the parameter correlations is supernova-driven baryon blowout or another process (such as a failure to capture baryons before cosmic reionization) that has the same effect. (2) Kormendy & Freeman (2014) suggest that there exists a large population of tiny halos that are essentially completely dark and that the discoverable galaxies at M_V -13 represent a smaller and smaller fraction of tinier DM halos. This has been suggested as the solution to the problem that the fluctuation spectrum of cold dark matter predicts more dwarfs than are observed in environments like the Local Group (e.g., Moore et al. 1999; Klypin et al. 1999).