


Stellar yields are a key ingredient in models of the chemical evolution of galaxies and stellar systems (Tinsley 1980; Gibson 1997; Romano et al. 2010; Nomoto et al. 2013). Core collapse supernova explosions release vast quantities of α-elements (e.g., O, Mg, Si, Ti) and Fe-peak elements into the Galaxy on relatively short timescales (≲ 107 years). Classical nova explosions (Romano & Matteucci 2003; Romano et al. 2010) and rapidly rotating massive stars may also be an important source of C, N, and heavy elements at the earliest times (Chiappini, Matteucci, & Meynet 2003; Chiappini et al. 2006; Hirschi 2007; Frischknecht et al. 2012).
Binary systems that explode as Type Ia supernovae are also responsible for producing substantial metals, mostly in the form of Fe (e.g., Seitenzahl et al. 2010), although Type Ia explosions typically take place on much longer timescales from a few hundred million years to a few gigayears (Matteucci & Greggio 1986). There is evidence that galaxies had a small number of prompt Type Ia explosions, which take place on much shorter timescales of ≈ 100 Myr since the beginning of star formation (Bonaparte et al. 2013). Together, massive stars, that explode as Type II supernovae, and Type Ia supernovae dominate the chemical evolution of many elements and for this reason AGB stars were until recently largely ignored in models of chemical enrichment (Matteucci & Francois 1989; Timmes et al. 1995; Gibson 1997; Kobayashi et al. 2006).
However, low- and intermediate-mass stars are a common inhabitant of galaxies and stellar systems and produce a copious amount of the gas and dust seen in the interstellar medium. In the last decade there has been considerable progress in our understanding of the nucleosynthesis of AGB stars. We now know that they produce considerable amounts of C, N, F, Na, the neutron-rich isotopes of Ne, Mg, as well as Na, Al, and heavy elements produced by the s-process. For a complete picture of the chemical evolution of galaxies, stellar yields from low- and intermediate-mass stars must be included.
5.1. Stellar yields from AGB stars
Renzini & Voli (1981) produced the first set of stellar yields from low- to intermediate-mass stars. These CNO yields were calculated with a fully synthetic evolutionary algorithm, which included HBB, TDU, and mass loss via the Reimers (1975) formula. Further contributions using synthetic AGB models have been made by Marigo et al. (1996), van den Hoek & Groenewegen (1997), Marigo (2001), Izzard et al. (2004), and Gavilán, Buell, & Mollá (2005). The biggest difference between the recent calculations listed above and those of Renzini & Voli (1981) is in the improved parameterisations of the AGB phase of evolution, based on detailed models with improved input physics. The latest synthetic models also use parameterisations that depend on the initial metallicity, which is something that Renzini & Voli's calculation did not do.
The increasing speed of modern computers means that the problem of running large grids of stellar models becomes time consuming, rather than impossible. There are now various compilations in the literature for yields from detailed AGB stellar models. Table 2 compiles these yields along with the mass and metallicity range, tells if they include predictions for s-process elements, and if downloadable yield tables are provided.
| Reference | Mass Range | Metallicity Range | s-process? | Downloadable |
| (in M⊙) | (in mass fraction, Z) | tables? | ||
| Fenner et al. (2004) | 2.5-6.5 | [Fe/H] = −1.4 | No | No |
| Herwig (2004b) | 2.0-6.0 | 1 × 10−4 | No | Yes |
| Karakas & Lattanzio (2007) | 1.0-6.0 | 1 × 10-4, 4, 8 × 10-3, 0.02 | No | Yes |
| Campbell & Lattanzio (2008) | 1.0-3.0 | Z = 0, [Fe/H] -6.5,-5.45,-4,-3 | No | Yes |
| Iwamoto (2009) | 1.0-8.0 | Z = 2 × 10-5 | No | No |
| Karakas (2010) | 1.0-6.0 | 1 × 10-4,4, 8 × 10-3, 0.02 | No | Yes |
| Siess (2010)(a) | 7.5-10.5 | 1 × 10-4 to 0.02 | No | Yes |
| Cristallo et al. (2011)(b) | 1.3-3.0 | 1 × 10-4 to 0.02 | Yes | Yes |
| Ventura et al. (2013) | 1.5-8.0 | 3 × 10-4, 10-3, 0.008 | No | No |
| Gil-Pons et al. (2013)(c) | 4.0-9.0 | 1 × 10-5 | No | Yes |
| Pignatari et al. (2013) | 1.5, 3.0, 5.0 | 0.01, 0.02 | Yes | Yes |
| Karakas et al. (2014) | 1.7, 2.36 | 3, 6 × 10-4 | Yes | Yes |
| Ventura et al. (2014) | 1-8.0 | 4 × 10-3 | No | No |
| Doherty et al. (2014a) | 6.5-9.0 | 0.004, 0.008, 0.02 | No | Yes |
| Doherty et al. (2014b) | 6.5-7.5 | 0.001, 1 × 10-4 | No | Yes |
| Straniero et al. (2014) | 4-6 | 0.0003, [α/Fe]=+0.5 | Yes | Yes |
| (a) Yields for six metallicities are provided with the range noted in the table. | ||||
| (b) Yields for nine metallicities are provided with the range noted in the table. | ||||
| (c) Downloadable tables are surface abundance predictions, yields are given in their Table 4. | ||||
There are other studies of low- and intermediate-mass stars that include stellar yields but are not included in Table 2 for the following reasons. Stancliffe & Jeffery (2007) perform a detailed study of the uncertainties affecting yields of low-mass AGB stars but only at one mass (1.5 M⊙, Z = 0.008). Church et al. (2009) present full s-process yields but also only for one mass (3 M⊙, Z = 0.02). We include only the most recent stellar yield predictions calculated by Ventura and collaborators from 2013 and 2014. Earlier calculations (e.g., Ventura et al. 2001; Ventura, D’Antona, & Mazzitelli 2002; Ventura & D’Antona 2008, 2009; Ventura & Marigo 2009; Ventura & D’Antona 2011) either use older input physics or cover a smaller range in mass and metallicity. There are also many papers that include surface abundances predictions for AGB models (a highly incomplete list includes the following examples: Kahane et al. 2000; Chieffi et al. 2001; Abia et al. 2002; Lebzelter et al. 2008; Weiss & Ferguson 2009; Campbell et al. 2010; Bisterzo et al. 2010; Kamath et al. 2012; D’Orazi et al. 2013) but not stellar yields; these are not included in Table 2.
The yields from Lagarde et al. (2011) are not included in Table 2 because they only include one isotope, 3He, although for a grid of low- and intermediate-mass models covering a large range in metallicity. Charbonnel & Lagarde (2010) examine the effects of extra mixing and rotation on the light-element yields of model stars up to 4 M⊙ but only provide yields for 7Li; we therefore do not include these in Table 2.
There are fewer yields for low-metallicity AGB stars below [Fe/H] ≤ −3 because of the difficulty of calculating the stellar evolution owing to the added complexity of proton ingestion episodes and mixing during the core He flash. Iwamoto (2009) and Campbell & Lattanzio (2008) present yields for low-metallicity AGB stars of [Fe/H] ≤ −3, and Gil-Pons et al. (2013) provide surface abundance predictions for intermediate-mass AGB and super-AGB stars at Z = 10-5 between M = 4 to 9 M⊙. Chieffi et al. (2001) present calculations of Z = 0 intermediate-mass (4 - 8 M⊙) AGB stars but no tabulated yields. No yields of s-process elements are available from very low-metallicity AGB models at the present (although see Campbell et al. 2010; Cruz et al. 2013).
Ideally, chemical evolution modellers would like a self-consistent set of AGB stellar yields covering a range in mass from ≈ 0.8 M⊙ to the limit for core collapse supernovae, ≈ 10 M⊙, for a broad range of metallicities, and for all elements from H through to Bi. In this context, none of the AGB yield sets mentioned is complete.
Some of these studies provide yields for a limited number of masses but for all elements up to bismuth (e.g., Cristallo et al. 2011; Pignatari et al. 2013). The yields by Siess (2010), Doherty et al. (2014a, 2014b), and Ventura et al. (2013) focus on light elements (up to Fe) for the mass range of stars that become super-AGB stars. The largest grid of detailed stellar yields for low- and intermediate-mass AGB stars in terms of the range of masses (1 - 6 M⊙), metallicities (Z = 0.0001, 0.004, 0.008, 0.02), and number of species (light elements up to Fe) is still Karakas (2010) but the yields of Ventura et al. (2013) cover almost the same range of masses, elements and metallicities (but not including solar).
5.2. Summary of elements produced by low and intermediate-mass stars
The stellar yields shown here are calculated according to
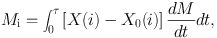 |
(4) |
where Mi is the yield of species i (in solar masses), dM / dt is the current mass-loss rate, X(i) and X0(i) refer to the current and initial mass fraction of species i, and τ is the total lifetime of the stellar model. The yield can be negative, in the case where the element is destroyed, and positive if it is produced.
It is still an open question whether low- and intermediate-mass stars contribute to the production of 7Li in the Galaxy (Romano et al. 2001; Travaglio et al. 2001b; Prantzos 2012). Prantzos (2012) concluded that primordial nucleosynthesis can produce at most only about 30% of the solar Li and that stellar sources (red giants, AGB stars, novae) must be responsible for at least half. Current stellar yields of Li from AGB stars do not support this production. The stellar yields by e.g., Karakas (2010) show that only a narrow mass range of intermediate-mass AGB stars produce more Li than they destroy. This occurs when the Li produced from HBB takes place at the period of highest mass loss. At Z = 0.02 this occurs at ≈ 5 M⊙. Super-AGB stars are also a possible source of Li (Ventura & D’Antona 2010; Ventura et al. 2013; Siess 2010; Doherty et al. 2014a).
There are many uncertainties involved in the production of 7Li in AGB models, including the mass-loss rates and the treatment of convective mixing (Ventura & D’Antona 2005a, 2005b; Iwamoto 2009). The stellar Li content initially rises dramatically from production through the Cameron-Fowler mechanism, but it then decreases slowly as the Li is cycled through the hot bottom of the envelope, resulting in its gradual destruction. Mass-loss rates for AGB stars, such as the formulae given by Vassiliadis & Wood (1993) and Blöcker (1995), have a superwind phase which occurs during the final few thermal pulses. The superwind phase results in a period of rapid mass loss, and most of the convective envelope is lost during this time. Thus the composition of the envelope at the start of the superwind phase critically determines the contribution that AGB stars make to the enrichment of the interstellar medium. By adjusting the mass-loss formula, one can manipulate the Li yield. In Figure 27 most of the 7Li has been destroyed by the time the superwind phase starts. Other factors that may influence the yields of Li include the presence of a binary companion, rotation, and the efficiency of extra mixing on the first and asymptotic giant branches (Charbonnel & Lagarde 2010; Lagarde et al. 2012).
5.2.2. Carbon, nitrogen, oxygen
AGB stars are one of the most important sources of 12C in the Galaxy. An estimate of the contribution of 12C from AGB stars suggests that they produce roughly one third of the Galaxy's inventory of 12C, providing roughly the same amount as core-collapse supernovae and Wolf-Rayet stars (Dray et al. 2003). These quantitative estimates are hindered by uncertainties in the depth and onset of the third dredge-up. Figure 34 shows yields from Karakas (2010) for 12C, 14N, 17O, and 19F for two metallicities. At Z = 0.02 production is dominated by models of about 3 M⊙, with no C production for models below about 2.5 M⊙. While it is difficult to determine masses for Galactic C stars, estimates point to stars with initial masses as low as about 1.5 M⊙ (Wallerstein & Knapp 1998) for the Galaxy. This suggests that C production is underestimated in the yields by Karakas (2010).
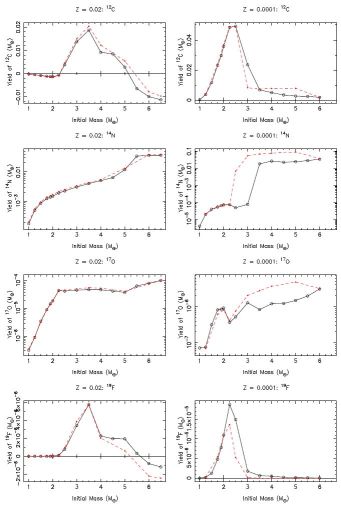 |
Figure 34. Stellar yields of 12C, 14N, 17O, and 19F as a function of the initial mass for models of Z = 0.02 (left-hand panels) and Z = 0.0001 (right-hand panels) from Karakas (2010). The solid line and open circles show results for the updated yields; the dashed line and closed circles show results from Karakas & Lattanzio (2007). The updated yields from Karakas (2010) use scaled-solar abundances, whereas the yields from Karakas & Lattanzio (2007) used non-solar C, N, and O to reflect the composition of the LMC and SMC. Reaction rates were also updated, which mostly affected 19F and 23Na. Also, we used Reimer's mass loss on the AGB in the M ≥ 3 M⊙, Z = 0.0001 models from Karakas (2010), whereas in Karakas & Lattanzio (2007) we used Vassiliadis & Wood (1993) on the AGB. |
The isotopes 13C and 14N are produced by the CNO cycles and mixed to the surface by first and second dredge-up prior to the AGB, and by HBB during the AGB. Figure 34 shows that the yields of N are dominated by intermediate-mass stars that experience HBB (see also Frost et al. 1998a; Chieffi et al. 2001; Pols et al. 2012). Chemical evolution models with AGB yields show that low-metallicity intermediate-mass stars play an essential role in the production of N along with massive rotating stars (e.g., Fenner et al. 2004; Romano et al. 2010; Kobayashi et al. 2011b).
Canonical AGB models do not produce substantial quantities of elemental O and stellar yields from such models are generally negligible, except at the lowest metallicities (e.g., at Z ≤ 10-4 Karakas & Lattanzio 2007; Campbell & Lattanzio 2008; Karakas 2010; Cristallo et al. 2011). Intermediate-mass stars of low metallicity can destroy a significant amount of 16O by HBB such that the surface oxgyen abundance decreases by 0.5 - 1.0 dex, depending on the stellar model (Ventura et al. 2013). The stellar yields by Pignatari et al. (2013), which include diffusive convective overshoot into the C-O core, suggest that low-mass AGB stars may be an important source of 16O in the Universe. Chemical evolution models that use these yields are needed to test the idea.
The only O isotope produced by canonical models is 17O which is produced by the CNO cycle during HBB. Kobayashi et al. (2011b) examined the evolution of the isotopic 16O / 17O and 16O / 18O ratios taking into account the contributions from Type II SNe and AGB stars. It was found that while the solar 16O / 18O ratio is well matched by current yields, the present-day ratio for 16O / 17O was too low, indicating an over-production of 17O by AGB models. This may put constraints on the rates of the 17O + p reactions, which are uncertain at stellar energies (e.g., Chafa et al. 2007; Sergi et al. 2010).
The cosmic origin of fluorine is not yet completely understood. Core collapse supernovae (Woosley & Weaver 1995) and stellar winds from Wolf Rayet stars (Meynet & Arnould 2000) are both predicted to release F-enriched material into the ISM, alongside AGB stars (Renda et al. 2004). Observationally, AGB stars and their progeny (e.g., post-AGB stars, planetary nebulae) are the only confirmed site of F production (Jorissen et al. 1992; Werner et al. 2005; Zhang & Liu 2005; Pandey 2006; Schuler et al. 2007; Abia et al. 2010; Lucatello et al. 2011), with no clear indication for enhanced F abundances resulting from the ν-process in a region shaped by past SNe (Federman et al. 2005). Recio-Blanco et al. (2012) noted that AGB stars are likely the dominant source of F in the cool main-sequence dwarfs they observed in the solar neighbourhood.
Figure 34 shows that F production is coupled with C production. Observations also show a clear correlation between [F/O] content and C/O in AGB stars (Jorissen et al. 1992, and Figure 22). The stellar yields follow a similar function in mass and metallicity space. This means that the uncertainties that are the most significant for C similarly affect F, although with the added complication that the reaction rates involved in F production in the He shell are rather uncertain as discussed in Section 3.5.
Kobayashi et al. (2011a) provide the most recent estimates of the chemical evolution of F using updated AGB yields as well as the latest ν-process yields from core-collapse SNe (see also Sánchez-Blázquez et al. 2012). The model by Kobayashi et al. (2011a) was able to reproduce the F abundances observed in field stars covering a range of metallicities, with SNe dominating production at the lowest metallicities (here using O as the tracer, [O/H] ≲ -1.2), followed by a rapid increase from AGB stars at around [O/H] ≈ -0.5.
The yields of elemental Ne from AGB stars are generally small, except in the case when substantial 22Ne is produced during thermal pulses (Karakas & Lattanzio 2003a). Kobayashi et al. (2011b) found that the contribution of AGB stars was essential for matching the solar Ne isotopic ratios (see also Gibson, Fenner, & Kiessling 2005). Without AGB stars the contribution from SNe dominate and produce too much 20Ne relative to the neutron-rich 21Ne and 22Ne.
Intermediate-mass AGB stars produce some Na via the Ne-Na chain (Forestini & Charbonnel 1997; Mowlavi 1999b; Ventura et al. 2013), although production is highly dependent on the uncertain rates of the 23Na + p reactions (Hale et al. 2004; Izzard et al. 2007). The AGB models used by Fenner et al. (2004) produced copious sodium and led to much larger [Na/Fe] abundances compared to observations of globular cluster stars (see also Gibson 2007). The stellar models in Karakas (2010) produced between ~ 6 to 30 times less Na compared to the stellar models in Karakas & Lattanzio (2007) as a result of using updated reaction rates. Figure 35 shows the difference for the Z = 0.004 models. Using the updated yields from Karakas (2010), Kobayashi et al. (2011b) found that AGB stars do not noticeably affect the chemical evolution of Na in the Milky Way Galaxy.
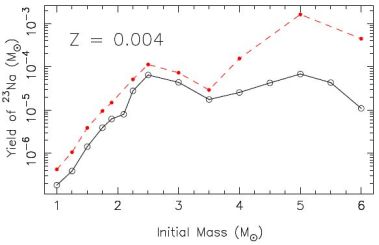 |
Figure 35. Stellar yields of 23Na as a function of the initial mass for models of Z = 0.004. The solid line and open circles show results from Karakas (2010), while the dashed line and closed circles show results from Karakas & Lattanzio (2007). |
The yields of Na and Al from AGB stars are also critically dependent on model assumptions and in particular on the convective model and temperature structure of the envelope (Ventura & D’Antona 2005a). While the Na and Al yields of Karakas (2010) are reasonably small, the yields from Ventura et al. (2013) suggest that intermediate-mass AGB and super-AGB stars may be substantial producers of Na and Al at low metallicities (Ventura et al. 2011).
The neutron-rich isotopes of Mg are produced by intermediate-mass AGB stars alongside core collapse SNe. The amounts of 25Mg and 26Mg produced by low-metallicity intermediate-mass AGB stars can be enough to affect the galactic chemical evolution of these isotopes. Fenner et al. (2003) found that the contribution of AGB stars was essential to explain the Mg isotopic ratios observed in cool evolved field stars (Gay & Lambert 2000; Yong et al. 2003b). Kobayashi et al. (2011b) noted that their chemical evolution model predicted higher than present-day solar ratios for 24Mg / 25, 26Mg using yields from AGB stars and SNe and concluded that AGB stars (or some other source, such as Wolf Rayet stars) need to produce more 25Mg and 26Mg.
Phosphorus and Sc can also be produced in small quantities by AGB stars as a consequence of neutron captures in the He intershell (Smith et al. 1987; Karakas et al. 2012). Most of the other intermediate-mass elements including Si, Cl, Ar, K, Mn are not significantly produced by AGB nucleosynthesis except for small isotopic shifts caused by neutron captures (Karakas et al. 2009). The predicted isotopic shifts, which include increases in the neutron-rich 29, 30Si, can be compared to measurements of the Si isotopes in pre-solar silicon carbide grains. We refer to Lugaro et al. (1999) and references therein for details (see also Zinner et al. 2006; Zinner 2008; Lewis et al. 2013).
5.2.5. Heavy elements produced by the s-process
The contribution from AGB stars is crucial to understand the origin and evolution of elements heavier than iron. About half of all heavy elements are produced by the s-process, and most of those elements are produced by AGB stars. One current uncertainty is the Galactic epoch at which AGB stars begin contributing toward the bulk Galactic chemical evolution of elements. Simmerer et al. (2004) suggested this epoch occurred around [Fe/H] ≳ -1, but that AGB stars can contribute inhomogeneously (locally) from [Fe/H] ≳ -3. This is also the metallicity at which CEMP stars with s-process elements become more common, compared to the CEMP stars without neutron-capture element overabundances, which dominate at lower metallicities (Beers & Christlieb 2005; Sneden et al. 2008; Frebel & Norris 2013).
Unfortunately, stellar yields from AGB stars that include predictions for heavy elements are even more incomplete than for light elements. The yields by Cristallo et al. (2011) include a complete network of elements to Bi for masses to 3 M⊙, these were extended to 4, 5, and 6 M⊙ AGB models for one metallicity (Z = 0.0003) by Straniero et al. (2014); Pignatari et al. (2013) include yields for three AGB masses at two metallicities (Z = 0.01 and 0.02); and Fishlock et al. (2014, submitted) present yields for M = 1 to 7 M⊙ at one metallicity, Z = 0.001. Lugaro et al. (2012) present tables of stellar abundance predictions as a function of thermal pulse number from models from 0.9 to 6 M⊙ for only one metallicity (Z = 0.0001 or [Fe/H] = − 2.3). The predictions from Lugaro et al. (2012) are not included in Table 2 because integrated yields are not provided.
For super-AGB stars the situation is even worse. The only s-process calculations currently published are for a single 9 M⊙, Z = 0.02 model in Karakas et al. (2012) and only for a limited nuclear network up to Mo. No yield tables were included with that study. Wanajo et al. (2011) calculate r-process yields from electron-capture SNe, which have evolved from super-AGB stars with massive O-Ne cores.
There have been various chemical evolution models that focus on the evolution of the neutron-capture elements and the contribution of AGB stars (e.g., Raiteri et al. 1999; Travaglio et al. 1999, 2001a, 2004; Fenner et al. 2006; Serminato et al. 2009; Hansen et al. 2013). In these models, the yields of s-process elements are included by extrapolating from the existing models, especially for intermediate-mass AGB stars where there are no or few existing theoretical predictions.
We comment on the production of s-process elements from intermediate-mass AGB stars. While the contribution from low-mass AGB stars to the chemical evolution of Ba and Pb is well supported by models and observations (Travaglio et al. 2001a), the contribution from intermediate-mass AGB stars has for some time been seen as minimal. For example, Travaglio et al. (2004) estimate that intermediate-mass stars contribute ≈ 8%, 6%, 6%, 1%, and 5% toward the solar-system composition of Sr, Y, Zr, Nb, and Mo, respectively. However, observational evidence suggests that intermediate-mass AGB stars produce substantial amounts of Rb (García-Hernández et al. 2006). Chemical evolution models are required, with a complete set of intermediate-mass and super-AGB yields, to quantitatively assess the impact of intermediate-mass stars on the chemical evolution of Rb.
We finish with a discussion of another uncertainty on stellar yield predictions: the effect of helium enrichment. Karakas et al. (2014) study the effect of helium enrichment on AGB evolution and nucleosynthesis for two masses (M = 1.7, 2.36 M⊙) at two metallicities appropriate for the GC ω Centauri (Z = 0.0003, 0.0006, which is roughly [Fe/H] ≈ −1.8 and − 1.4, respectively). An increase of ΔY = 0.10 at a given mass decreases the yields of C by up to ≈ 60%, of F by up to 80%, and the yields of the s-process elements Ba and La by ≈ 45%. The main reason is that an increase of ΔY = 0.10 leads to roughly a factor of 3 decrease in the amount of dredged up material during the AGB. The lifetimes of He-enriched models are significantly shorter than their counterparts with primordial He content, which means that they will contribute to the chemical evolution of a system sooner.
It may not be enough to simply evolve grids of stellar evolutionary sequences covering a range in mass and metallicity. Variations in the helium mass fraction have a significant impact on the stellar yields and may be an important third parameter. This reminds us of the days before the primordial He abundance was determined, and stellar models were typically published with a spread of Y values.