

Cosmology has finally become a mature science during the past decade, with predictions now routinely confirmed by observations. The modern cosmological theory is known as ΛCDM – CDM for Cold Dark Matter, particles that moved sluggishly in the early universe and thereby preserved fluctuations down to small scales (Blumenthal et al. (1984), see Fig. 1), and Λ for the cosmological constant (e.g., Lahav et al. (1991)). A wide variety of large-scale astronomical observations – including the Cosmic Microwave Background (CMB), measurements of baryon acoustic oscillations (BAO), gravitational lensing, the large-scale distribution of galaxies, and the properties of galaxy clusters – agree very well with the predictions of the ΛCDM cosmology.
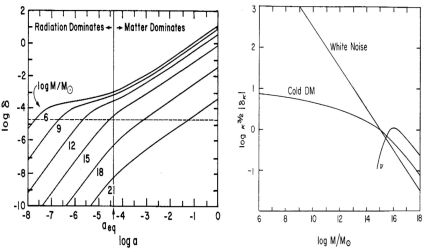 |
Figure 1. The origin of the CDM spectrum of density fluctuations. Left panel: Fluctuations corresponding to mass scales 106 M⊙, 109 M⊙, etc., grow proportionally to the square of scale factor a when they are outside the horizon, and when they enter the horizon (cross the horizontal dashed line) the growth of the fluctuation amplitude δ is much slower if they enter when the Universe is radiation dominated (i.e., a < aeq). Fluctuations on mass scales > 1015 M⊙ enter the horizon after it becomes matter dominated, so their growth is proportional to scale factor a; that explains the larger separation between amplitudes for such higher-mass fluctuations. (From a 1983 conference presentation Primack and Blumenthal (1984), reprinted in Primack (1984).) Right panel: The resulting CDM fluctuation spectrum (κ3/2 |δκ| = ΔM / M) is contrasted with a δ ∝ κ0 white noise (Poisson) spectrum with the same power at all wavelengths (where wave number κ is as usual related to wavelength λ by κ = 2π/λ), and with the hot dark matter spectrum if the dark matter were light neutrinos (ν) which is cut off on galaxy mass scales by free-steaming. (From Blumenthal et al. (1984). This calculation assumed that the primordial fluctuations are scale-invariant (Zel'dovich) and that Ωmatter = 1 and Hubble parameter h = 1.) |
Like the standard model of particle physics, the ΛCDM standard cosmological model requires the determination of a number of relevant cosmological parameters, and the theory does not attempt to explain why they have the measured values – or to explain the fundamental nature of the dark matter and dark energy. These remain challenges for the future. But the good news is that the key cosmological parameters are now all determined with unprecedented accuracy, and the six-parameter ΛCDM theory provides a very good match to all the observational data including the 2015 Planck temperature and polarization data Planck Collaboration et al. (2015a). Within uncertainties less than 1%, the Universe has critical cosmic density – i.e., Ωtotal = 1.00 and the Universe is Euclidean (or "flat") on large scales. The expansion rate of the Universe is measured by the Hubble parameter h = 0.6774 ± 0.0046, and Ωmatter = 0.3089 ± 0.0062; this leads to the age of the Universe t0 = 13.799 ± 0.021 Gyr. The power spectrum normalization parameter is σ8 = 0.816 ± 0.009, and the primordial fluctuations are consistent with a purely adiabatic spectrum of fluctuations with a spectral tilt ns = 0.968 ± 0.006, as predicted by single-field inflationary models Planck Collaboration et al. (2015a). The same cosmological parameters that are such a good match to the CMB observations also predict the observed distribution of density fluctuations from small scales probed by the Lyman alpha forest 1 to the entire horizon, as shown in Fig. 2. The near-power-law galaxy-galaxy correlation function at low redshifts is now known to be a cosmic coincidence Watson et al. (2011). I was personally particularly impressed that the evolution of the galaxy-galaxy correlations with redshift predicted by ΛCDM Kravtsov et al. (2004) turned out to be in excellent agreement with the subsequent observations (e.g., Conroy et al. (2006)).
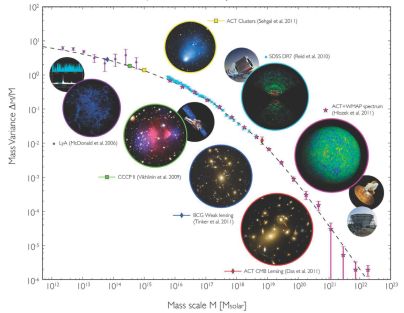 |
Figure 2. The r.m.s. mass variance ΔM / M predicted by ΛCDM compared with observations, from CMB and the Atacama Cosmology Telescope (ACT) on large scales, brightest cluster galaxy weak lensing, clusters, the SDSS galaxy distribution, to the Lyman alpha forest on small scales. This figure highlights the consistency of power spectrum measurements by an array of cosmological probes over a large range of scales. (Redrawn from Fig. 5 in Hlozek et al. (2012), which gives the sources of the data.) |
For non-astronomers, there should be a more friendly name than ΛCDM for the standard modern cosmology. Since about 95% of the cosmic density is dark energy (either a cosmological constant with ΩΛ = 0.69 or some dynamical field that plays a similar cosmic role) and cold dark matter with ΩCDM = 0.26, I recommend the simple name "Double Dark Theory" for the modern cosmological standard model Primack and Abrams (2006), Abrams and Primack (2011). The contribution of ordinary baryonic matter is only Ωb = 0.05. Only about 10% of the baryonic matter is in the form of stars or gas clouds that emit electromagnetic radiation, and the contribution of what astronomers call "metals" – chemical elements heavier than helium – to the cosmic density is only Ωmetals ≈ 0.0005, most of which is in white dwarfs and neutron stars Fukugita and Peebles (2004). The contribution of neutrino mass to the cosmic density is 0.002 ≤ Ων ≤ 0.005, far greater than Ωmetals. Thus our bodies and our planet are made of the rarest form of matter in the universe: elements forged in stars and stellar explosions.
Potential challenges to ΛCDM on large scales come from the tails of the predicted distribution functions, such as CMB cold spots and massive clusters at high redshifts. However, the existing observations appear to be consistent thus far with predictions of standard ΛCDM with standard primordial power spectra; non-Gaussian initial conditions are not required Planck Collaboration et al. (2015b). Larger surveys now underway may provide more stringent tests.
1 The Lyα forest is the many absorption lines in quasar spectra due to clouds of neutral hydrogen along the line of sight to the quasar. Back.