


In this section, I will review the three physical processes that are able to produce extended and bright Lyα emission: i) recombination radiation following hydrogen photoionization (by a quasar or star forming galaxy), ii) "continuum-pumping" or Lyα scattering of the photons produced in the quasar broad-line-region or within the Interstellar Medium (ISM) of a star forming galaxy, and iii) Lyα collisional excitation and recombination radiation following collisional ionization (so called Lyα cooling radiation). All these mechanisms require the presence of "cool" gas (i.e., with temperatures well below 105 K). In addition, recombination radiation and "continuum-pumping" also require that the gas is "illuminated" by the quasar or by some other bright source of UV photons. In this case, the resulting Lyα emission is sometimes called "fluorescent" in the literature (e.g., Cantalupo et al. 2005, Kollmeier et al. 2010, Cantalupo et al. 2012, 2014; Borisova et al 2016).
In this case, Lyα photons are produced in a (photo-)ionized medium as a consequence of radiative recombination cascades and the Lyα emissivity will be simply proportional to the hydrogen recombination rate times the ionized hydrogen density squared. Because the hydrogen recombination rate has a relatively mild dependence from temperature, i.e. about linear (e.g., Osterbrock 1989) around 104 K, this is the easiest case to model. The actual number of Lyα photons produced by each recombination event (and therefore by each ionizing photon, in photoionization equilibrium) will depend on the details of the recombination cascades that populate the 2 P2 state that will decay to the 1 S2 producing a Lyα photon. A good approximation, even in the low-density Intergalactic Medium, is to assume that every Lyman-line photon from n > 2 levels is converted into lower series photons plus either Lyα or two-photon continuum (Case B approximation, Baker & Menzel 1938). In this case, the fraction of Lyα photons for each recombination event ranges between 0.68 and 0.61 for 104 < (T / K) < 104.7 (Cantalupo et al. 2008) showing again only a mild dependence on temperature. For reference, in the opposite case (Case A) when all Lyman-series photons leave the cloud, the fraction of Lyα photons for each recombination will be reduced by about a half. Combining these information with the Case B hydrogen recombination coefficient, one can obtain the effective Lyα recombination coefficient αLyαeff for Case B, that can be approximated with the expression (Cantalupo et al. 2008):
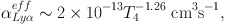 |
(1) |
where, T4 = 104 K, for 103 < (T / K) < 104. For a fully ionized cloud of hydrogen and helium, the Lyα integrated volume emissivity is therefore:
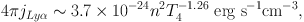 |
(2) |
where n is the gas density in units of atoms per cm−3. For a uniform gas slab with depth L in units of kpc at redshift z, the observed surface emissivity - equivalent to the surface brightness ignoring radiative transfer effects - will be given therefore by:
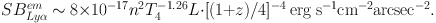 |
(3) |
The observed values of the SB of giant Lyα nebulae range from a few times 10−18 erg s−1 cm−2 arcsec−2 in the external parts (at distances of 50-100 kpc from the central sources or the central peak of the Lyα emission) to 10−16 erg s−1 cm−2 arcsec−2 in the central regions. From this simple calculation, it is easy to understand that the observed SB would inevitably require large gas densities (n > 0.1) in order to be explained by pure recombination emission. These high density estimates were obtained and claimed since the discoveries of the first nebulae around radio-loud quasars and galaxies (e.g. Heckman et al. 1991).
Are these densities compatible with our picture of cold gas within massive halos? It is instructive to rewrite the previous expression rewriting the density n in terms of the baryonic overdensity with respect to the canonical value of 200 for collapsed objects (δ200). Making use of the definition of clumping factor, i.e. CL = < n2 >L / < n >L2 where the average is made over a cylinder with depth L and projected area of 1 arcsec2 on the sky, we obtain:
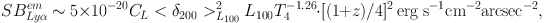 |
(4) |
where L100 = L / 100 kpc. In this formula, no assumptions have been made about the density distribution and density inhomogeneities are encoded in the clumping factor term CL. Assuming that 100 kpc is the typical projected length of the cold gas distribution in the halo, it is then straightforward to see that, even if all the halo gas is in the form of a fully ionized and uniform medium at T = 104 K, the predicted SB will be smaller than the observed values by several orders of magnitude. In this case, the observed SB constrains the clumping factor on scales corresponding to 1 arcsec2 on the sky plane, i.e. on a square with side of about 7 kpc at z ∼ 3 and on 100 kpc along the line of sight to be at least CL ∼ 20−2000. This simple estimates is confirmed by detailed radiative transfer and cosmological simulations, e.g. Cantalupo et al. (2014). For a series of small clouds with uniform density in a empty medium, the clumping factor is equal to the inverse of the volume filling factor fv, and therefore the implied values of fv are smaller than 10−3 and likely much lower (i.e., 10−4 − 10−5), considering that, if a hot medium is present as it should be in these massive halos, most of the mass and density will be in the hot component rather than the cold one used for the estimate above. These small filling factors would imply again that the individual densities of the clouds should be higher than n > 0.1 and likely closer to n ∼ 1−10 cm−3 considering the presence of a hot medium.
A similar analysis can be made considering the total Lyα luminosity, see e.g. the classical approach used by McCarthy et al. (1990). In this case, integrating the Lyα emissivity given above one would simply obtain:
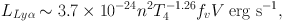 |
(5) |
where V is the total volume in cm3, or more conveniently expressed in terms of the halo virial masses:
 |
(6) |
where M12 is the virial mass in units of 1012 M⊙. In this case, the value of fv in the literature is typically fixed to the one derived from extended line emission in local AGN (10−6 to 10−4, e.g. Heckman et al. 1989). McCarthy et al. (1990) adopted fv to 10−5 "as a guess", as reported in their paper, and this value was then adopted later in the literature as a sort of "standard" value. As discussed above, our SB consideration lead to similar values. Once fv is fixed, the individual densities of the clouds are therefore constrained to be of the order of 1-100 cm3 given the Lyα luminosities obtained by the various studies in the literature (1043 < LLyα / (erg s−1) < 1045) and assuming that the nebulae are associated with massive halos (1 < M12 < 10). Interestingly enough, similar densities are required in the pure recombination case to explain the reported limits on He II emission compared to Lyα for some cases, e.g. for the Slug Nebula (Arrigoni-Battaia et al. 2015) and for the MUSE radio-quiet quasar nebulae (Borisova et al. 2016).
The analysis above shows that recombination radiation is a viable scenario to explain the observed Lyα luminosities and SB if the nebulae are composed by dense (n > 1 cm−3), highly ionized and cold (T ∼ 104) clumps with volume filling factors smaller than 10−3 or, analogously, if the gas clumping factor is larger than about a thousand on projected scales with size of about 5-8 kpc. Assuming that such a population of clouds - not resolved by current cosmological simulation - do exists within massive halos, we should examine if they can be indeed ionized by the observed sources within or around the Lyα Nebulae. The required ionizing luminosities Qion are simply derived using photoionization equilibrium and considering that about 68% of recombinations produce Lyα photons (Case B) at T ∼ 104 as discussed above:
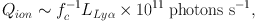 |
(7) |
where fc is the covering factor of the gas as seen by the ionizing source. Assuming fc ∼ 1 this would imply that the required ionization luminosities to explain the Lyα emission of the giant Lyα nebulae (1043 < LLyα / (erg s−1) < 1045) are in the range 1054−1056 s−1. These ionization luminosity could be explained easily by AGN, even with modest luminosities, or by starbursts with star formation rates of at least a few hundred to few thousand solar masses per year (depending on the ionizing photon escape fraction from the galaxy ISM and on the stellar Initial Mass Function, e.g. Leitherer et al. 1999). As a reference, the quasar associated with the Slug Nebula, the largest and more luminous Lyα nebula discovered to date (Cantalupo et al. 2014) has an expected Qion ∼ 1057.5 photons s−1 using the measured rest-frame UV luminosity and assuming a standard for this type of quasars (e.g., Lusso et al. 2015). Given the ubiquity of AGN and massively star forming galaxies (traced, e.g. in submm) within or around giant Lyα nebulae, there are therefore enough ionizing photons for the recombination scenario. In section 4, I will review the possible origin of the illuminated gas in terms of kinematical signatures of inflows or outflows.
3.2. Continuum pumping (scattering)
Due to the resonant nature of the Lyα emission, the detected photons from extended nebulae may also "originate" from the ISM of embedded galaxies or from the broad line region of the associated AGN, rather than being produced "in situ" by recombination processes. A "scattering" scenario for some nebulae and in particular for LABs have been proposed in the past as a possible origin of the level of polarization detected in some sources, e.g. in SSA22-LAB1 by Hayes et al. (2011) and Beck et al. (2016), and in a radio-galaxy nebula by Humphrey et al. (2013). In other cases, radio-quiet nebulae imaged in polarization failed to show any detectable level of polarization, e.g. Prescott et a. (2011). Theoretical prediction for the level of polarization produced by scattering by a central sources have been presented, e.g. by Dijkstra & Loeb (2008) using idealized geometries and velocity fields and extended recently to radiative hydrodynamics simulations by Trebitsch et al. (2016). These models suggest that scattering from a central source is able to produce a larger and steeper polarization profile with respect to scattering by photons produced by "in situ" processes, such as collisional excitation. Comparison with the data cannot clearly exclude one of these two scenarios but current data, at least for SSA22-LAB1, seems more compatible with a "in situ" Lyα photon production rather than scattering from a "central" source.
In case a significant fraction of Lyα photons detected in the extended nebulae are produced by scattering from the "central" source, then all the estimates of masses and densities based on the assumption of pure recombination emission discussed above should be revised. The "scattering" contribution will be of course related to the density of neutral hydrogen atoms (nH0) rather than the ionized density squared as in the recombination case. The Lyα optical depth at line center is given by:
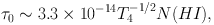 |
(8) |
where N(HI) is the neutral hydrogen column density in units of cm−2. As an example, using the estimated hydrogen ionization rates of the Slug Nebula quasar (UM287), i.e. Γ ∼ 7.7 × 10−9 at distances of 100 kpc, we can derive N(HI) in the simple case of uniform small clouds with individual densities of n and filling factor fv exposed to ionizing radiation as discussed in the previous section. In photoionization equilibrium, the averaged neutral fraction of hydrogen along a path of length L from the quasar will be given by:
 |
(9) |
where the last term is valid at T ∼ 104K, α(T) is the hydrogen recombination coefficient ( ∼ 3 × 10−13 at T4 ∼ 1), L is the length in units of kpc. Because the N(HI) column density up to a length L is given in this case by N(HI, L) = < xeq >L· n · fv · L, then the Lyα optical depth at line center is simply:
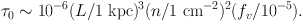 |
(10) |
Assuming that most of the scatterings are produced at line center, then a continuum photon produced by the AGN is only scattered into Lyα at distances larger than 100 kpc from the source, even for large clump densities. These distances are only reduced by about a factor of two for sources that are ten times fainter than UM287. Because most of the emission is concentrated in the inner parts, scattering contribution in the case the gas is illuminated by the ionizing radiation of a source should be therefore negligible and recombination radiation should be the dominant mechanism.
The only case in which scattering may be the dominant production mechanism of the large Lyα emission of the giant nebulae is when the central source is not highly ionizing the gas but still producing copious amounts of Lyα and continuum photons slightly blueward of Lyα. In this case, studied numerically by, e.g. Cantalupo et al. (2014), the gas will be mostly neutral and the optical depths will become very large. The scattering will be extremely efficient and the main problem with this scenario would be to transport out to hundred kpc scales, as observed for the Lyα Nebula, the photons that are resonantly trapped in the inner regions. During scattering, the Lyα photons will perform a random walk both in space and in frequency. Unless the parameters are fine tuned, most of the scatterings in space will be very close to each other and the photons will escape, with a single fly-out, only when scattered in the wings of the line spectral distribution. In order to transport out these photons to another scattering location and increase the size of the Nebula, the column densities need to be large enough to produce scattering in the wings of the line, i.e. N(HI) > 1021 cm−2, resulting in much larger column densities and masses of neutral gas with respect to what observed in absorption around quasars (e.g. Prochaska et al. 2013; see also Cantalupo et al. 2014 for discussion). Although scattering and a mostly "neutral" scenario for the gas seems less plausible than recombination emission to explain the origin of giant Lyα nebulae, observations of non-resonant lines such He II 1640 and hydrogen Hα from giant Lyα Nebulae may be used in the next future to better constrain the scattering contribution to the emission.
3.3. Collisional Excitation (cooling)
When both neutral hydrogen and free electrons are present and the electron temperature is around a few times 104 K, the collisional excitation rate of Lyα (qLyα) may be several orders of magnitude larger than the Lyα effective recombination rate (see, e.g. Cantalupo et al. 2008) and therefore produce in principle very strong Lyα emission from lower density gas. Differently than the recombination case, however, the collisional excitation rates are a very strong function of temperature, with an exponential decline for temperatures lower than a few times 104K dropping strongly below the recombination rate just below T ∼ 104 K. On the other hand, when the electron temperature approaches 105 K collisional ionization dominates over collisional excitations. As a result, collisional excitation is a very efficient process to produce Lyα photons in a partially ionized medium only for electron temperatures around 2−5 × 104 K. In absence of photoionization and heating sources, e.g. in collisional ionization equilibrium, radiative losses (cooling) due to collisional excited Lyα would quickly reduce the electron temperature effectively suppressing further Lyα emission. A source of heating is therefore required in order to balance the Lyα cooling effects. On the other hand, if heating brings electron temperatures close to 105 K, Lyα collisional excitation would be suppressed again, therefore the heating source should be fine tuned in order to produce a stable supply of Lyα emission with collisional excitation.
Since the discovery of the Steidel's LABs in SSA22, a numerous series of theoretical and numerical papers have addressed the possibility that these nebulae - apparently lacking a source of ionization - could be powered instead by Lyα cooling (including, e.g., Haiman et al 2001, Fardal et al. 2001, Furlanetto et al. 2005, Dijkstra & Loeb 2009, Goerdt et al. 2010, Faucher-Giguere et al. 2010, Rosdahl & Blaizot 2012). The suggested source of heat in all these studies is given by the conversion of the gravitational potential energy due to cosmological accretion of gas into massive dark matter halos. Alternative sources of energy such as galactic superwinds have been also proposed by Taniguchi & Shioya (2000) with a similar energy budget with respect to the gravitational accretion case but also sharing the same limitations as discussed below.
A simple estimate of the energy associated with cosmological gas accretion for a Navarro-Frenk-White profile with concentration parameter c = 5 gives (Faucher-Giguere et al. 2010):
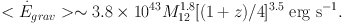 |
(11) |
For Lyα nebulae associated with very massive halos with M ∼ 1013 M⊙, this order of magnitude estimate for the potential energy is interestingly close to the observed Lyα emission. In our standard picture for the formation of these massive halos, we think however that a significant fraction of this potential energy should result in the formation of a hot gaseous halo with temperatures of the order of T ∼ 107 K as a result of the virial shocks. At these temperatures, the gas would more slowly lose energy by other radiation channels rather than Lyα, e.g., free-free continuum radiation in the Extreme UV and X-ray, and, once the temperature decreases, further energy may be radiated away via line emission from He II or from heavier elements, if present. Analytical and numerical models in the past ten years have nonetheless suggested that some fraction of the densest accreting material could not form a stable shock and therefore could cool and produce Lyα (e.g. Dekel & Birnboim 2006). Cooling Lyα emission models have therefore introduced an efficiency factor that takes into account how much of the potential energy is dissipated by this cold gas phase and required that this efficiency factor is at least few tens of percent in order to obtain enough Lyα photons. Unfortunately, it is very difficult to predict the value of this efficiency factor as it would depend on the details of accretion and cosmological structure formation and on a very accurate estimate of the ionization and temperature state of the gas. Depending on these details, many questions remain open about how and where within the halo the potential energy (or the energy produced by galactic superwinds) could be dissipate in form of Lyα.
The majority of the models discussed so far ignore however that sources of ionization do exist within all nebulae observed to date. In most cases, as I have reviewed in section 2, these sources are AGN or massively star forming galaxies. The estimated ionization rates show that there are enough ionizing photons to power the nebulae and therefore it seems current clearer that a pure Lyα cooling origin of the nebulae is not necessarily required by the majority of the observations. This may be confirmed by duty cycle arguments and comparing the number densities of quasars, radio-galaxies and overdense regions where LABs are found as discussed in previous section (see also Borisova et al. 2016 and Overzier et al. 2013 for further discussion). Questions however remain about the possible contribution of collisional Lyα emission to recombination radiation as this would have important consequences on the estimates of densities and masses of the nebulae. Addressing these questions would likely require a new generation of theoretical and numerical models able to resolve the physics and the small scales associated with dense regions within massive halos and, at the same time, the interplay between the gas and the local radiation sources (e.g., in terms of photoionization, photo-heating and feedback).