Observational Diagnostics of Gas Flows: Insights from Cosmological Simulations

2. ABSORPTION DIAGNOSTICS

We divide our discussion of absorption diagnostics into different observational statistics.

Covering fractions of absorbers within different impact parameters from foreground galaxies have been extensively modeled using simulations and provide the most basic consistency test between simulations and observations. Over the last decade, large observational datasets on absorption by the CGM gas flows has been assembled using quasar spectra transverse to galaxies of different types and at different redshifts. For example, this technique has been applied at both low and high redshifts to foreground dwarf galaxies (e.g., Bordoloi et al., 2014b), damped Lyα absorbers (e.g., Rubin et al., 2015), luminous red galaxies (e.g., Gauthier et al., 2010), ∼ L^⋆ star-forming galaxies (e.g., Adelberger et al., 2003; Tumlinson et al., 2011; Rudie et al., 2012; Turner et al., 2014), and quasars (e.g., Hennawi et al., 2006; Prochaska et al., 2013). In a study of z ∼ 2−3 Lyman break galaxies (LBGs), Steidel et al. (2010) also demonstrated that useful constraints on the CGM can be extracted from spectra of ordinary, fainter background galaxies (see also Bordoloi et al., 2011). With the advent of 30-m class ground-based telescopes in the next decade, spectroscopy of background galaxies will become increasingly powerful as it becomes generically possible to obtain spectra of multiple sight lines through the halos of individual foreground galaxies.

Lyman limit systems (LLSs; usually quantitatively defined as systems with HI column density N_HI ≥ 10^17.2 cm⁻²) in particular are useful tracers of inflows and outflows, being dense enough to be closely associated with galaxy halos but not sufficiently dense to arise only in galactic disks. ¹ Cosmological simulations show that LLSs are good tracers of cool filamentary accretion, especially at high redshift (z ∼ 2−4) where these are most prevalent (e.g., Fumagalli et al., 2011; Faucher-Giguère & Kereš, 2011; Kimm et al., 2011; Goerdt et al., 2012; Shen et al., 2013; Fumagalli et al., 2014; Faucher-Giguère et al., 2015).

Radiative transfer is important to properly model LLSs since these systems are optically thick at the Lyman limit by definition. However, until recently most cosmological simulations computed ionization balance assuming that all systems are optically thin. In early studies using simple approximations for the ionization state of the gas, (e.g., Dekel et al. 2009 though see Kimm et al. 2011), the predicted covering fractions of cold accretion streams were well in excess of observational constraints (Steidel et al., 2010). Properly processing simulations with ionizing radiative transfer – thus allowing more accurate identification of strong HI absorbers – showed that the LLS covering fractions of cold accretion streams are in fact quite small in simulations. As a result, the predicted small LLS covering fractions of cold accretion streams are consistent with present observational constraints (≲ 10% for LBG-mass halos at z ∼ 2; Faucher-Giguère & Kereš, 2011; Fumagalli et al., 2011).

The more accurate treatments of radiative transfer actually revealed tension in the opposite direction. In an analysis of high-resolution quasar spectra transverse to z ∼ 2−2.5 LBGs, Rudie et al. (2012) measured an LLS covering fraction within a projected virial radius of 30 ± 14%, at face value a factor ∼ 3 higher than cosmological simulations without strong galactic winds (Faucher-Giguère & Kereš, 2011; Fumagalli et al., 2011). This discrepancy has been plausibly resolved in the latest generation of cosmological simulations with stronger stellar feedback, necessary to produce realistic galaxy stellar masses (Fumagalli et al., 2014; Faucher-Giguère et al., 2015). These simulations showed that ≳ 50% of the cool halo gas giving rise to LLSs around z ∼ 2−3 LBGs arises not from IGM accretion but rather from galactic winds. Figure 1 shows two simulations of the same low-mass LBG halo, one with strong galactic winds and one without galactic winds, at z = 2−4.

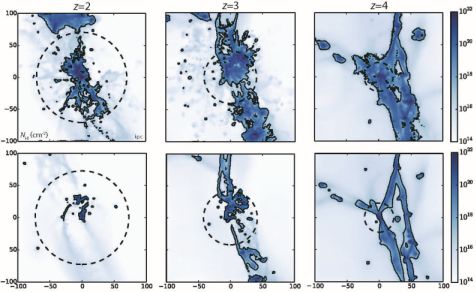Figure 1. Top: H I maps for a low-mass LBG simulation with stellar feedback from the FIRE project at z = 2, 3, and 4 (M_h(z = 2) = 3 × 10¹¹ M_⊙). Bottom: Simulation from the same initial conditions but without galactic winds. The virial radius of the halo is indicated in each panel by the dashed circles and Lyman limit systems are indicated by solid contours. Stellar feedback increases the covering fractions in galaxy halos both by directly ejecting cool gas from galaxies and through the interaction of galactic winds with cosmological inflows. At z = 2, LLSs in this example are almost exclusively restricted to galaxies and their immediate vicinity absent galactic winds. Length scales are consistent across rows and columns. Adapted from Faucher-Giguère et al. (2015).

Galactic winds enhance LLS covering fractions in the simulations in two ways: 1) they eject cool interstellar gas into the CGM, and 2) they increase the cross section of inflows through hydrodynamic interactions. Importantly, it is not only the galactic wind from the central galaxy that interacts with infalling gas, but also outflows from nearby satellites. The latter effect is enhanced because satellites tend to be embedded in surrounding large-scale structure filaments. These filaments are “puffed up” by galactic winds from embedded galaxies. It is apparent from the example in Figure 1 that, absent galactic winds, the z ∼ 2 LLS covering fraction from accreting gas is very small and almost entirely limited to galaxies and their immediate vicinity (at higher redshifts, where the halos are less massive, the filamentary inflows give rise to more extended LLSs). This is because cool filamentary inflows tend to disappear in higher mass, lower redshift halos (e.g., Kereš et al., 2005; Dekel & Birnboim, 2006). Most latest-generation cosmological simulations, including those from the EAGLE (Schaye et al., 2015), Illustris (Vogelsberger et al., 2014), and FIRE (Hopkins et al., 2014) ² projects, implement on-the-fly approximations based on local gas properties for self-shielding based on post-processing radiative transfer calculations (Faucher-Giguère et al., 2010; Fumagalli et al., 2011; Rahmati et al., 2013).

A current puzzle are the order unity LLS covering fractions measured in the halos of luminous quasars z ∼ 2−2.5. Prochaska et al. (2013) reported an LLS covering fraction f_cov(> 10^17.2; < R_vir) ≈ 0.64_−0.07^+0.06 within a projected virial radius of z ∼ 2−2.5 quasars (see also Prochaska et al., 2014). This high LLS covering fraction should be compared to the lower fraction f_cov(10^17.2; < R_vir) = 0.30 ± 0.14 measured by Rudie et al. (2012) around z ∼ 2−2.5 Lyman break galaxies (LBGs) in the Keck Baryonic Structure Survey (KBSS). The LBGs in KBSS reside in dark matter halos of characteristic mass M_h ≈ 10¹² M_⊙ (Adelberger et al., 2005a; Trainor & Steidel, 2012), a factor just ∼ 3 × lower than quasars. Using cosmological zoom-in simulations with stellar feedback but neglecting AGN feedback, Fumagalli et al. (2014) and Faucher-Giguère et al. (2015) found simulated LLS covering fractions consistent with those measured in LBG halos (see also Shen et al. 2013). In both studies, however, the most massive simulated halos failed to explain the LLS covering fraction measured around quasars by a large factor, suggesting that the presence of a luminous AGN could affect the properties of CGM gas on ∼ 100 kpc scales.

More recent simulations by Rahmati et al. (2015) and Faucher-Giguère et al. (2016) were able to match the covering fractions observed by Prochaska et al. (2013) in quasar halos, but for different reasons. Recognizing that the distribution of halo masses probed by quasars is only crudely constrained by clustering measurements, Rahmati et al. (2015) made the optimistic assumption that all of Prochaska et al. (2013)'s quasars are hosted in halos of mass greater than the characteristic clustering mass M_h ≈ 3 × 10¹² M_⊙. They then compared the quasar observations with the halos in the EAGLE simulation with mass above this threshold as a function of impact parameter in absolute units of proper distance. As a result, many of Rahmati et al. (2015)'s simulated LLSs are located at a smaller fraction of the virial radius than would be inferred assuming a constant virial radius corresponding to the characteristic quasar clustering halo mass (the assumption made in Prochaska et al. 2013). Since covering fractions decreases with increasing impact parameter, Rahmati et al. (2015)'s approach tends to boost the covering fractions, enough to bring them in agreement with those observed around real quasars. Rahmati et al. (2015)'s fiducial simulation included AGN feedback, but AGN feedback does not appear to play a significant role in explaining their results. Faucher-Giguère et al. (2016)'s simulations, on the other hand, are consistent with the f_cov(> 10^17.2; < R_vir) value reported by Prochaska et al. (2013). Faucher-Giguère et al. (2016)'s simulations, from the FIRE project, included strong stellar feedback but no AGN feedback. Relative to the analysis of Faucher-Giguère et al. (2015), which focused on LBG-mass halos, Faucher-Giguère et al. (2016) analyzed a much larger set of quasar-mass halos (15 vs. 1) and the new halos were simulated at order-of-magnitude better mass resolution than the previous quasar-mass halo.

Figure 2 summarizes how the simulated LLS covering fractions of Faucher-Giguère et al. (2015) and Faucher-Giguère et al. (2016) compare with observed covering fractions at z ∼ 2−2.5. For both LBG and quasar halos, the simulations rely on star formation-driven galactic winds to explain observations. Faucher-Giguère et al. (2016) performed a resolution convergence study of the covering fractions in quasar-mass halos, and found two important results. The first is that LLS covering fractions increase with increasing resolution. This is the primary reason why Faucher-Giguère et al. (2015)'s earlier quasar-mass run fell short of reproducing observations. The second is that much of the LLS material in quasar-mass halos is due to galactic winds not from central galaxies but instead from lower-mass satellite galaxies. This is illustrated in Figure 3, which shows that the spatial distribution of LLSs in quasar-mass halos correlates strongly with the spatial distribution of satellites. As in lower-mass halos, galactic winds from satellites both eject gas into the CGM and increase the cross section of large-scale structure filaments. The velocity maps in Figure 3 show that the LLS structures with embedded satellites are typically infalling, so these LLS are connected to galactic accretion, albeit somewhat indirectly.

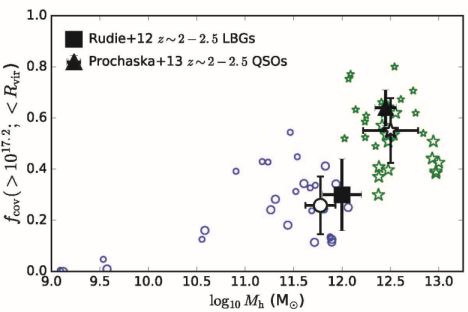Figure 2. Blue circles: Lyman limit system (LLS) covering fractions within a projected virial radius for the high-resolution simulated halos from the FIRE project analyzed in Faucher-Giguère et al. (2015). For each simulated halo, covering fractions for 25 snapshots over the redshift interval z = 2−2.5 are shown. The simulations are in good agreement with LLS covering fractions measured around LBGs in that redshift interval by Rudie et al. (2012) (black square). Green stars: Covering fractions at z = 2 (large) and z = 2.5 (small) for the quasar-mass halos analyzed in Faucher-Giguère et al. (2016). The quasar-mass simulated halos are compared to LLS measurements transverse to luminous quasars at z ∼ 2−2.5 by Prochaska et al. (2013) (black triangle). The open black symbols show averages over simulated LBG-mass halos and QSO-mass halos, with the error bars showing the standard deviations of the simulated data points included in the averages. Figure from Faucher-Giguère et al. (2016).

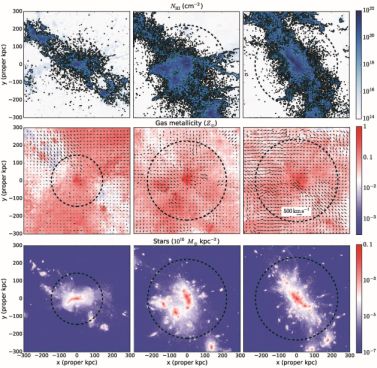Figure 3. H I column density (top), gas-phase metallicity (middle) and stellar mass surface density (bottom) maps for three representative quasar-mass halos from the FIRE project at z = 2 (from left to right: M_h(z = 2) = (2.4, 8.8, 9.9) × 10¹² M_⊙). The virial radius is indicated by dashed circle in each panel and solid contours indicate Lyman limit systems. The vectors on metallicity maps indicate projected mass-weighted velocities. The large-scale distribution of LLS gas correlates with the spatial distribution of satellite galaxies, indicating the importance of stellar feedback from satellites in producing large HI covering fractions. The velocity maps also show that the LLS structures with embedded satellites are typically infalling. Figure from Faucher-Giguère et al. (2016).

The gas particle mass in Faucher-Giguère et al. (2016)'s simulations of quasar-mass halos is m_b ≈ 3 × 10⁴ M_⊙. At this resolution, Figure 2 shows that the simulations are in good agreement with observations of massive halos. Since these covering fractions are not far from unity, they are necessarily saturating with increasing resolution. However, a comparison with lower-resolution simulations indicates that the CGM properties of quasar-mass halos may not be fully converged even in the highest-resolution simulations presently available. The stringent resolution requirements are in part due to the necessity of resolving the generation of galactic winds from satellites. Since the high simulated covering fractions in Fu et al. (2016) do not require AGN feedback, one prediction is that similarly massive halos without a quasar – such as may be selected based on high stellar mass or SFR - should show similarly high covering fractions. In an analysis of three sight lines with impact parameter ∼ 100−200 proper kpc from z ∼ 2−2.5 sub-millimeter galaxies (SMGs), Fu et al. (2016) did not find compelling evidence for LLS-strength absorbers. If the simulations are correct and this observational result persists when the SMG sample is increased, it would suggest that some SMGs are hosted by halos significantly less massive than luminous quasars at z ∼ 2. A larger observational sample is, however, clearly needed to firm up the statistical significance of this observational result.

The ability to develop robust observational diagnostics of galactic accretion depends critically on the ability of numerical codes to properly capture the hydrodynamics of gas accretion, so we briefly digress to comment on this issue. In the example shown in Figure 1, cold streams (as traces by LLSs) disappear in a slightly lower-mass halo (M_h(z = 2) = 3 × 10¹¹ M_⊙) than predicted by some previous simulations (see, e.g., the simulations similar-mass halos in Faucher-Giguère & Kereš, 2011) because older smooth particle hydrodynamics (SPH) simulations underestimated the destructive effects of shocks and hydrodynamical instabilities (Agertz et al., 2007; Sijacki et al., 2012; Nelson et al., 2013). Recent improvements to SPH algorithms (e.g., Read & Hayfield, 2012; Saitoh & Makino, 2013; Hopkins, 2013; Hu et al., 2014) have greatly reduced the major historical differences with respect to grid-based codes, particular for fluid mixing instabilities. Overall, cold streams falling into galaxy halos tend to be more rapidly disrupted by hydrodynamic interactions with halo gas in codes of improved accuracy. The morphological differences in cold gas properties between hydrodynamic solvers are largest around the halo mass M_h ∼ 3 × 10¹¹ M_⊙ above which quasi-static hot atmospheres start to develop. In lower-mass halos, cold streams are generically present in halos simulated using different numerical methods, at least at z = 2, which has been the subject of the most detailed simulation analyses. Interestingly, the most important differences overall for gas accretion between older SPH codes and grid-based codes are in the amount of “hot mode” accretion, i.e. the amount of hot gas that cools from hot atmospheres. Hot accretion is significantly more efficient in grid codes and updated SPH codes because spurious heating from the dissipation of turbulent energy on large scales prevents the same behavior in traditional SPH codes (Nelson et al., 2013). It is important to note, though, that most of the relevant direct code comparisons were performed on simplified cosmological simulations without strong galactic feedback. Observations of galaxy clusters clearly show that intra-cluster gas must be heated (likely by AGN feedback) to prevent a cooling catastrophe and avoid SFRs order-of-magnitude in excess of those observed in brightest cluster galaxies (e.g., McNamara & Nulsen, 2007; Fabian, 2012). This heating suppresses hot mode accretion. It is not yet clear how much different numerical methods for hot mode accretion diverge when realistic feedback is included. Comparing the predictions of simulations with observations will continue to play a critical role in identifying limitations of the simulations.

Before closing this section, we note that observations provide significantly more detail on the distribution of neutral hydrogen in galaxy halos than captured by the LLS covering fractions emphasized above, including better statistics on the incidence of (more numerous) lower-column absorbers and their line-of-sight velocity distributions (e.g., Rudie et al., 2012). More comprehensive comparisons with simulations will be necessary to fully exploit the discriminating power of these observations for galactic inflow and outflow models.

2.2. Metal Absorption Systems Transverse to Galaxies

Metal absorption is commonly observed out to ∼ 0.5−1 R_vir transverse to foreground galaxies of different types (e.g., Adelberger et al., 2005b; Steidel et al., 2010; Chen, 2012; Werk et al., 2013; Bordoloi et al., 2014b; Liang & Chen, 2014; Lau et al., 2016). However, gas that is first accreting from the IGM is expected to be relatively metal-poor (e.g., van de Voort & Schaye, 2012). In cosmological simulations with relatively weak stellar feedback, Fumagalli et al. (2011) found that the mean metallicity of cold streams in M_h ∼ 10¹⁰ − 10¹² M_⊙ halos at z = 1.3−4 is ∼ 0.01 Z_⊙, weakly dependent on halo mass and redshift. Similarly, Goerdt et al. (2012), concluded that cold streams will be challenging to detect in metal line absorption due to their low-metallicity and small covering fractions. The low-metallicity cold streams found in simulations severely under-predict the metal line equivalent widths observed around LBGs, strongly suggesting that most of the metal absorption observed transverse to LBGs originates from gas that has been processed by galaxies, such as galactic winds. Indeed, Turner et al. (2015) used photoionization modeling to argue that at least some of the metal-enriched gas (≳ 0.1 Z_⊙) observed around z ∼ 2.3 star-forming galaxies arises in the hot phase of galactic winds. In a few instances where abundance ratios have been measured, metal-rich CGM absorbers have abundance ratios consistent with either core collapse (e.g., Lau et al., 2016) or Type Ia supernovae (e.g., Zahedy et al., 2016). Cosmological simulations also convincingly demonstrate that star formation-driven galactic winds are necessary to explain metals observed in the CGM (e.g., Shen et al., 2012; Hummels et al., 2013; Suresh et al., 2015; Liang et al., 2016; Ford et al., 2016; Turner et al., 2016).

Despite the association between metal-rich gas and outflows, there is no clear cut metallicity division between inflows and outflows. In § 2.1, we emphasized how galactic winds from infalling satellites can puff up large-scale structure filaments. Thus, a good fraction of the gas first accreting onto galaxies may come into contact with metal-enriched material. The extent to which this metal-enriched gas contaminates galactic accretion depends on how efficiently metals mix in the CGM. While simulations provide some indication of the expected mixing, observations of closely spaced sight lines toward gravitationally lensed quasars and photoionization modeling show that metal absorption systems are often compact and poorly mixed (e.g., Rauch et al., 1999; Rauch et al., 2001; Simcoe et al., 2006; Schaye et al., 2007; Crighton et al., 2015). Overall, cool metal absorbers have inferred sizes ranging from ∼ 1 pc to ≳ 1 kpc, with some evidence that typical size increases with increasing ionization state. Some clouds may be less than a solar mass in mass.

All numerical methods are limited in their ability to capture metal mixing near their resolution limit. While grid codes tend to over-mix metals due to diffusive errors at the grid scale, ³ standard SPH codes “lock” metals into SPH particles. Because of this, it is often assumed that SPH under-mixes metals. However, this is only true for metal clumps above the resolution limit: tiny metal clumps below the resolution limit will appear over-mixed in SPH codes because their metals will be spread over the gas mass of individual SPH particles. For reference, state-of-the-art zoom-in SPH simulations of Milky Way-mass galaxies have typical gas particle masses ∼ 10⁴−10⁵ M_⊙ (Shen et al., 2013; Stinson et al., 2013; Hopkins et al., 2014). Thus, even state-of-the-art SPH simulations likely underestimate metal mixing in the CGM in at least some circumstances. In such circumstances, sub-resolution SPH models that attempt to model metal diffusion owing to unresolved turbulence (e.g., Shen et al., 2010) could vitiate rather than improve the solution. An important question for future work will be to identify the kinds of CGM absorbers that can be reliably resolved in cosmological simulations. If metal absorbers are compact because supernova ejecta take a long time to mix with ambient gas, then absorption by hydrogen and helium (elements synthesized in the Big Bang) may not suffer from the same clumpiness effects. Warm and hot gas phases, which tend to be more volume-filling, may also be easier to resolve in simulations. OVI, now routinely detected at both low and high redshift (e.g., Tumlinson et al., 2011; Lehner et al., 2014; Turner et al., 2015), stands out as one particular ion for which it will be important to determine the convergence properties of cosmological simulations.

Upcoming observations of multiple sight lines through the halos of individual galaxies will provide useful information regarding the size scales of different CGM absorbers. The best local laboratory to carry out such an experiment is M31. Lehner et al. (2015) recently analyzed 18 sight lines within 2 R_vir ≈ 600 kpc of M31, thus producing a partial map of the multi-phase CGM around the galaxy. New HST/COS observations of quasars behind M31 as part of the AMIGA (Absorption Maps In the Gas of Andromeda) project (PI N. Lehner) will improve on this pilot analysis with a total of 25 sight lines within 1.1R_vir. While these observations will not constrain structure on the fine scales possible with gravitationally lensed quasars or photoionization modeling, the spatially resolved map of M31's CGM will help us better interpret observations of single sight lines through the halos of similar-mass galaxies, such as those from the COS-Halos program (Tumlinson et al., 2011). One caveat with drawing inferences based on detailed studies of a single system, however, is that simulations show that the CGM can be quite dynamic and time variable (e.g., Faucher-Giguère et al., 2015; Hafen et al., 2016). Thus, such observational analyses will be most powerful when combined with simulations that can inform how the observational inferences can be generalized to other halos. Another approach for observationally constraining the size scale of CGM structures is to quantify the fraction of the area of a background source absorbed by foreground CGM clouds. Quasar accretion disks have diameters ∼ 0.01 pc while galaxies generally have half-light radii ≳ 1 kpc. Thus, background galaxies probe absorber size scales larger than background quasars (e.g., Diamond-Stanic et al., 2016).

2.3. Down-the-Barrel Metal Absorption Lines

Another observational approach to detect galactic accretion is to use single “down-the-barrel” spectra of galaxies (e.g., Steidel et al., 2010; Rubin et al., 2012; Martin et al., 2012). One advantage of the down-the-barrel observations, relative to galaxy pairs, is that gas that absorbs stellar light from a galaxy is known to be located between the galaxy and the observer. Thus, redshifted absorption can be unambiguously associated with gas with a radial velocity component in the direction of the galaxy. ⁴ Down-the-barrel observations, however, suffer from a different difficulty due to the fact that the typical infall velocity of IGM accretion is comparable to the halo velocity. ⁵ Thus, even for sight lines fortuitously aligned with infalling CGM cool gas, absorption from the infalling gas will typically overlap in velocity space with interstellar medium (ISM) gas. Since ISM gas is expected to be generally both denser and more enriched with metals than cold streams, down-the-barrel absorption by cold streams will typically appear as a minor perturbation to ISM absorption (Kimm et al., 2011). ⁶ In detailed analyses of down-the-barrel spectra, Rubin et al. (2012) and Martin et al. (2012) reported detections of infalling gas in a small fraction, ∼ 3−6%, of z ∼ 0.4−1.4 galaxies. These detections were made using low-ionization metal absorption lines and thus likely trace relatively metal-rich gas, such as infalling dwarf galaxies on their way to merging or recycling wind gas, rather than gas accreting from the IGM for the first time. Unfortunately, there has been relatively little modeling of the inflow signatures expected in down-the-barrel observations. Despite the challenges in using this technique for probing IGM accretion, more modeling would very valuable given the very rich observational datasets now available, which may make it possible to extract even subtle signatures.

2.4. Kinematic and Azimuthal Angle Diagnostics

A simple toy physical picture for inflows and outflows is one in which inflows from the IGM bring in the angular momentum that creates rotating galactic disks and in which galactic winds have a bi-conical morphology due to collimation normal to the galactic plane. If this toy model were correct, it would suggest that absorption by gas normal to the plane of disk galaxies should arise primarily from galactic winds, while absorption in the disk plane may be commonly due to infalling gas. In this picture, the infalling gas would typically co-rotate with the disk as it approaches the galaxy. Thus, a combination of azimuthal angle and kinematic diagnostics would constitute a powerful probe of inflows and outflows. This is indeed a promising avenue for identifying inflows and outflows, with some observational support for physical differences between planar and extra-planar absorbers in the CGM of galaxies. However, the latest high-resolution cosmological simulations indicate that the character of both galactic accretion and galactic winds change significantly with redshift and galaxy mass (e.g., Muratov et al., 2015; Hayward & Hopkins, 2015). Observations also show that galactic winds become significant weaker as star formation activity in galaxies declines from its peak at z ∼ 2 (e.g., Steidel et al., 2010) to the present (e.g., Heckman & Borthakur, 2016). Thus, it is likely that the toy model outlined above is too simple, and this is an area where more detailed and systematic modeling is likely to prove critical.

Azimuthal Angle Diagnostics

Observationally, there is support for galactic winds preferentially expanding normal to the plane of disk galaxies from spectroscopic observations transverse to foreground galaxies (expressed in terms of azimuthal angle relative the semi-minor axis of the galaxy projected on the sky; Bordoloi et al., 2011; Bouché et al., 2012; Kacprzak et al., 2012) and from down-the-barrel spectra of galaxies as a function of inclination angle of the disk (Kornei et al., 2012; Rubin et al., 2012; Rubin et al., 2014; Martin et al., 2012; Bordoloi et al., 2014a). Figure 4 shows observations of each type for z ∼ 0.5−1.5 galaxies in zCOSMOS. The larger average Mg II absorption equivalent widths along the poles of disk galaxies suggest that strong polar Mg II absorbers trace galactic winds. Because down-the-barrel sight lines toward low-inclination disk galaxies probe regions of the CGM similar to transverse spectra at small azimuthal (polar) angles, we will refer to both types of observations as probing the azimuthal angle dependence of CGM gas in what follows. ⁷ In Mg II absorption, the observed azimuthal angle dependence appears to be stronger for systems with high rest equivalent widths W₀ ≳ 1 Å. This is consistent with an origin of strong MgII absorbers in galactic winds, which is also supported by other observations (e.g., Ménard & Chelouche, 2009; Nestor et al., 2011; Matejek & Simcoe, 2012). Recently, Kacprzak et al. (2015) reported evidence that OVI absorbers in the CGM of 0.08 ≤ z ≤ 0.67 galaxies arise primarily either along their minor axis or their major axis, with stronger absorbers being preferentially found along the minor axis.

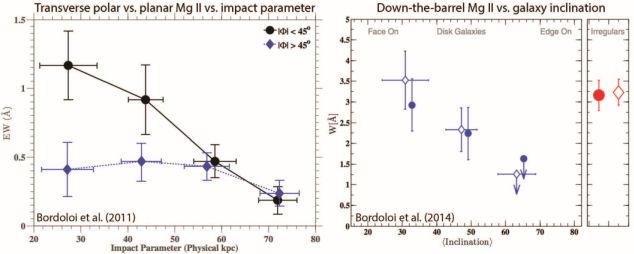Figure 4. Examples of how observed Mg II absorption varies as a function of azimuthal angle relative to the semi-minor axis of a galaxy and as a function of inclination angle in down-the-barrel spectra of galaxies. Left: Average Mg II equivalent width around 0.5 ≤ z ≤ 0.9 zCOSMOS disk galaxies as a function of impact parameter along the disk axis (| φ | < 45^∘) vs. near the disk plane (| φ | > 45^∘; Bordoloi et al., 2011). Right: Average MgII equivalent width vs. inclination from co-added down-the-barrel spectra of zCOSMOS 1 ≤ z ≤ 1.5 galaxies (Bordoloi et al., 2014a). The circles and diamonds correspond to two different ways of making the measurement. These observations are consistent with galactic winds preferentially expanding normal to the plane of disk galaxies but there has been so far relatively little modeling of these observations.

Most existing observations of azimuthal angle dependence are at low to intermediate redshift, z ≲ 1.5. This is in part because these observations require high-resolution imaging of the foreground galaxy in order to measure inclination or azimuthal angle. At high redshift, this requires long integrations with either HST or adaptive optics. In an analysis of the rest-frame optical morphological properties of z ∼ 2−3 star-forming galaxies, Law et al. (2012) concluded that in contrast to galaxies at lower redshifts, there is no evidence for a correlation between outflow velocity and galaxy inclination. On the other hand, Newman et al. (2012) found 3σ evidence in a sample of 27 z ∼ 2 star-forming galaxies with spatially resolved spectroscopic data that the mass loading factors of galactic winds are higher in face-on galaxies. It will be interesting to expand studies of azimuthal angle dependence in this redshift regime.

From the theoretical standpoint, it is possible that any azimuthal dependence present at lower redshift will be either weaker or absent in the CGM of z ≳ 2 galaxies. First, z≳2 star-forming galaxies are often observed to have clumpy morphologies, especially in the UV light that traces star formation (e.g., Förster Schreiber et al., 2011), and galactic winds are to a large extent driven by outflows from prominent star-forming clumps (e.g., Genzel et al., 2011; Bordoloi et al., 2016). Chaotic and clumpy galaxy morphologies at high redshift followed by the gradual emergence of stable disks are also a generic finding of recent cosmological simulations (e.g., Agertz et al., 2009; Ceverino et al., 2010; Hopkins et al., 2014; Oklopcic et al., 2016; Ma et al., 2016b; Ceverino et al., 2016). Thus, there may simply often not be well-defined gaseous disks to neatly collimate galactic winds at high redshift. Furthermore, at z ∼ 2 SFRs can be elevated relative to the local Universe by up to ∼ 2 orders of magnitude, and some simulations suggest that galactic wind bursts may be sufficiently powerful to expel most of the ISM from galaxies (e.g. Muratov et al., 2015). In that case, even if it were present, a gaseous disk may not offer enough resistance to significantly collimate the galactic wind.

Overall, azimuthal angle dependence is a promising approach for separating inflows and outflows statistically, but a more systematic analysis of the predictions of galaxy formation simulations will be needed to inform when a significant azimuthal angle dependence is expected. The left panel of Figure 5 shows an example of how the metallicity of CGM gas varies with azimuthal angle in the Eris2 simulation of a Milky Way progenitor at z = 2.8 (Shen et al., 2013). In this example, gas is substantially more metal enriched above and below the galaxy due to the effects of galactic winds, but it remains to be shown whether this simulation is representative.

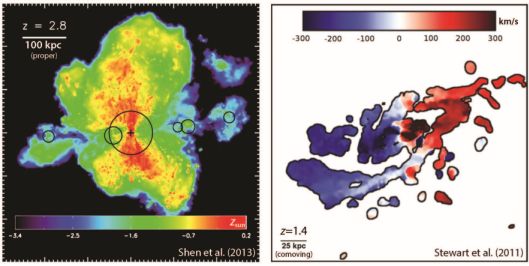Figure 5. Simulations that suggest the potential of azimuthal angle and kinematic diagnostics of galactic accretion. Left: Projected gas metallicity in the Eris2 simulation at z = 2.8. In this image, the stellar disk is nearly edge-on and the metal-enriched gas entrained by the galactic wind forms a rough bi-cone above and below the disk. The circles show virial radii, including of the five most massive nearby dwarf galaxies, which are aligned in the direction of metal-poor infalling filaments (adapted from Shen et al. 2013). Right: Line-of-sight velocity map of cool halo gas (N_HI > 10¹⁶ cm⁻²) for a simulated Milky Way-mass halo at z = 1.4. The cool halo gas tends to rotate in the same direction as cool halo gas out to R ≳ 40 proper kpc (100 co-moving kpc). Both results shown here are based on zoom-in simulations of single halos, so more work is needed to determine which aspects generalize to different halo masses, assembly histories, redshifts, and details of how the baryonic physics is modeled. Adapted from Stewart et al. (2011).

Kinematic Diagnostics

Weaker Mg II absorbers can arise from either inflows or outflows, but kinematics can potentially distinguish different origins. Several simulations indicate that accreting cool gas preferentially joins galactic disks in a co-rotating structure, consistent with galactic disks acquiring angular momentum from the accreting gas Kereš & Hernquist (2009); Brooks et al. (2009); Stewart et al. (2011); Stewart et al. (2013); Kauffmann et al. (2016); Stewart et al. (2016). ⁸ Because the infalling gas co-rotates with the galaxy, its distribution is expected to be at least mildly flattened along the galactic semi-major axis. The right panel shows an example of a zoom-in simulation of a Milky Way-mass halo at z = 1.4 in which the radial velocity profile of the cool halo gas with HI column N_HI > 10¹⁶ cm⁻² indicates co-rotation with the growing galactic disk out to R ≳ 40 proper kpc (Stewart et al., 2011).

Observationally, there are several tentative detections of co-rotating MgII absorbers at low and high redshifts (e.g., Steidel et al., 2002; Kacprzak et al., 2010; Bouché et al., 2013; Bouché et al., 2016), but current observational samples are small and conflicting results have been reported (e.g., Kacprzak et al., 2011). The simple picture of co-rotating MgII absorbers tracing galactic accretion is no doubt complicated by the different possible origins of MgII absorbers, including outflows, which can also carry angular momentum imparted as they are launched from a rotating disk. Over the next several years, kinematic diagnostics of halo gas will become increasingly interesting with the advent of a new generation of integral field surveys, including MaNGA (Bundy et al., 2015), KMOS^3D (Wisnioski et al., 2015), and with MUSE (e.g., Bacon et al., 2015), which will provide a new handle on the internal kinematics of galaxies. As with azimuthal angle diagnostics, systematically analyzing simulation predictions for the kinematics of gas galactic accretion relative to the orientation and internal kinematics of galaxies for a wide range of redshifts and galaxy properties will be critical to make progress. Currently, our theoretical expectations are limited by the small number of simulated halos for which kinematic relationships have been analyzed in detail, with existing studies being typically limited to a one or a few zoom-in simulations.

2.5. Cosmological Absorber Statistics

All the observational diagnostics discussed so far rely on an association between absorbing gas and a galaxy. However, quasar absorption spectra contain a wealth of information on intergalactic absorbers without known galaxy associations. Nevertheless, many of the stronger absorption systems in the spectra of arbitrarily selected quasars arise in the CGM of foreground galaxies and thus provide important statistical constraints on galactic accretion.

The HI Column Density Distribution

We saw in § 2.1 that LLSs in galaxy halos arise from a mix of inflows and outflows. Thus, LLSs from galactic accretion contribute to the observed HI column density distribution. Using a simulation from the OWLS project post-processed with radiative transfer, van de Voort et al. (2012) quantified the contribution of cold accretion flows to the observed z = 3 HI column density distribution. The simulation analyzed by van de Voort et al. (2012) reproduces the observed HI column density distribution over ten orders of magnitude in N_HI (Altay et al., 2011). In this simulation most LLSs arise within galaxy halos and most of these are infalling toward a nearby galaxy. On this basis, van de Voort et al. (2012) concluded that cold accretion flows predicted by cosmological simulations have been statistically detected in the observed HI column density distribution at z = 3. The argument is compelling, though there are some caveats that future simulations and observational analyses should attempt to address to firm up the conclusion. Observationally, measurements of the column density distribution are relatively uncertain in the LLS regime (e.g., Prochaska et al., 2010), in part because LLSs are on the flat part of the curve of growth. Theoretically, the simulation results summarized in § 2.1 indicate that galactic winds can contribute comparably to – or even dominate over – cold accretion streams in explaining LLSs in galaxy halos at z ∼ 2−2.5. Since the properties of galactic winds are uncertain, it is plausible that reasonable agreement with the observed column density distribution could be obtained absent cold streams for some wind models. Finally, a combination of resolution effects and numerical limitations of different hydrodynamic solvers introduces additional uncertainties in the theoretical predictions (Bird et al., 2013; Nelson et al., 2013; Nelson et al., 2016).

The Metallicity Distribution of LLSs

Recently, Lehner et al. (2013) and Wotta et al. (2016) reported evidence that the metallicity distribution of randomly selected LLSs at z < 1 is bimodal, with dearth of LLSs with metallicity of about ten percent solar. ⁹ These authors interpreted the high-metallicity branch as arising in outflows, recycling winds, and tidally stripped gas around galaxies, while the low-metallicity branch may trace cool, dense accreting gas. If this interpretation is correct, then LLS metallicity would be an extremely powerful way to identify cool galactic accretion at z < 1. At z > 2, the observational analyses of Fumagalli et al. (2016b); Lehner et al. (2016), and Glidden et al. (2016) indicate instead a broad unimodal distribution of LLS metallicities.

Motivated by the low-redshift observations of Lehner et al. (2013) and Wotta et al. (2016); Hafen et al. (2016) analyzed the LLS metallicity distribution at z < 1 using a sample of zoom-in simulations from the FIRE project. To model the cosmological distribution from a sample of zoom-in simulations, Hafen et al. (2016) convolved the LLS properties for individual halos with the dark matter halo mass function. In these simulations, LLSs are concentrated close to galaxies at z < 1 so this halo-based approach should capture the majority of LLSs; Hafen et al. (2016) showed that it reproduces the LLS cosmological incidence measured by Ribaudo et al. (2011). Figure 6 summarizes the key results from Hafen et al. (2016) regarding the LLS metallicity distribution, and the relationship of LLS metallicity with inflows and outflows defined based on instantaneous radial kinematic relative to central galaxies. The analysis indicates that high-velocity outflows (with radial velocity exceeding the halo circular velocity by a factor ≳ 2) tend to have higher metallicities ([X/H] ∼ −0.5) while very low-metallicity LLSs ([X/H] < −2) are typically associated with IGM inflows. However, most LLSs occupy an intermediate region in metallicity-radial velocity space. Overall, the simulated LLS metallicity distribution does not show significant evidence for bimodality. The strong overlap between instantaneous inflows and outflows for intermediate metallicity systems is in part due to the prevalence of wind recycling in the FIRE simulations at z < 1, which causes metal-rich galactic wind ejecta to later fall back onto galaxies (Anglés-Alcàzar et al., 2016). The lack of a clean bimodality in the simulated LLS metallicity distribution is also due to the fact that halos covering the broad mass range M_h ∼ 10¹⁰ − 10¹² M_⊙ contribute significantly to the distribution. Since the ISM and CGM metallicities both increase with galaxy mass in the simulations (Ma et al., 2016a; Muratov et al., 2016), any narrow feature in the metallicity distribution is likely to be washed out in the cosmological average. One effect that could cause simulations to miss features in the metallicity distribution is the mixing of metals on small scales. As mentioned above, some observations indicate that metals can be locked in compact clumps that will not be resolvable in cosmological simulations for the foreseeable future (e.g., Schaye et al., 2007). Going forward, it will be useful to address this issue by supplementing cosmological simulations with higher-resolution calculations better suited to understand small-scale mixing. The analysis of Hafen et al. (2016) included only 14 simulated main halos, so it will also be important to firm up the statistical significance of the results. Furthermore, it will be interesting to use simulations to study in more detail the redshift evolution of LLS metallicities, as well as how the metallicity distribution changes with HI column, e.g. from LLSs to DLAs. Cooper et al. (2015) analyzed the z = 3.5 LLS metallicity distribution in a full-volume cosmological simulation with the Illustris galaxy formation model (Vogelsberger et al., 2013; Torrey et al., 2014) and also found a broad unimodal distribution.

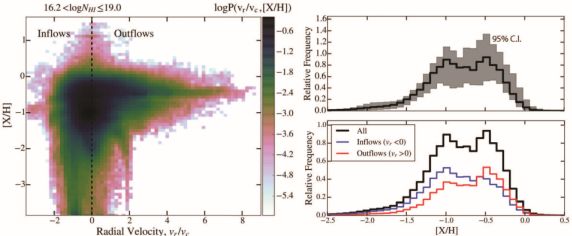Figure 6. Properties of the cosmological distribution of (randomly selected) LLSs at 0 < z < 1 computed by convolving a suite of zoom-in simulations from the FIRE project with the dark matter halo mass function. Left: Relative incidence (logarithmic units) of LLSs with 10^16.2 < N_HI ≤ 10¹⁹ cm⁻² in the metallicity vs. radial kinematics plane (radial velocity v_r defined relative to the central galaxy of the halo hosting the LLS and expressed in units of halo circular velocity). High-velocity outflows (with radial velocity exceeding the circular velocity by a factor ≳2) tend to have higher metallicities ([X/H] ∼ −0.5) while very low-metallicity LLSs ([X/H] < −2) are typically associated with gas infalling from the IGM. Right: The corresponding overall LLS metallicity distribution. In the top panel, the gray region shows the 95% confidence interval resulting from the limited number of zoom-in simulations included in the analysis. There is no significant evidence for multiple modes in the simulated metallicity distribution. In the bottom panel, the total metallicity distribution is divided between gas elements that are instantaneously inflowing (v_r < 0) and outflowing (v_r > 0) relative to their central galaxy. The inflowing and outflowing distributions overlap strongly in part because wind recycling is efficient at low redshift, so metal-enriched outflows are later identified as instantaneous inflows. Adapted from Hafen et al. (2016).

¹ Galactic disks are better traced by damped Lyα absorbers (DLAs; N_HI ≥ 2 × 10²⁰ cm⁻²; e.g., Wolfe et al. 2005; Neeleman et al. 2015). At very high redshift, the increased cosmic mean density and declining cosmic ultraviolet background (UVB) cause absorbers of fixed HI column to probe structures more closely associated with the low-density IGM with increasing redshift (e.g., McQuinn et al., 2011). As a result, LLSs become associated with structures such as intergalactic filaments and some DLAs may arise in the CGM. There rapid increase in LLS incidence observed at z≳3.5 suggests that LLSs commonly arise outside galaxy halos at these redshifts (Fumagalli et al., 2013) while the rapid evolution of the DLA metallicity distribution at z≳5 suggest that DLAs at these redshifts commonly arise outside galaxies (Rafelski et al., 2014). Back.

² See the FIRE project web site at http://fire.northwestern.edu. Back.

³ Such errors are mitigated in moving-mesh codes in which grid cells are advected with the flow, such as Arepo (Springel, 2010), as well as in the “meshless finite mass” (MFM) method implemented in GIZMO (Hopkins, 2015). Back.

⁴ In galaxy pair experiments, an outflowing absorber located behind the foreground galaxy would also appear redshifted. This introduces a generic ambiguity in the interpretation of absorption lines transverse to foreground galaxies. Back.

⁵ Absent hydrodynamic interactions and angular momentum, the radial velocity would be simply equal to the velocity of free fall into halo. Current cosmological simulations indicate that asymptotic cold stream radial velocities are typically closer to half the halo circular velocity (Kereš et al., 2005; Goerdt & Ceverino, 2015). Back.

⁶ If the stellar light of a galaxy were concentrated in a point source and the ISM were rotating in perfectly circular motion around the center, then the ISM would move purely tangentially with respect to the light source and could not mimic infalling gas. In real galaxies, stellar light is however spatially extended and the internal dynamics and morphology of the ISM can be quite complex. For example, at z ∼ 2 the nebular line emission of galaxies is often very clumpy (e.g., Förster Schreiber et al., 2009). These effects could cause some ISM gas to appear as infalling. Back.

⁷ Note, however, that the two types of observations are not equivalent since down-the-barrel spectra are always sensitive to high-density material near (or within) the target galaxy, while transverse spectra only probe the CGM at distances from the galaxy equal to the impact parameter or greater. Back.

⁸ This is not to say that infalling cool gas solely determines the angular momentum of disk galaxies. In an analysis of the Illustris simulation, Zjupa & Springel (2016) identify the important roles of specific angular momentum transfer from dark matter onto gas during mergers and from feedback expelling low specific angular momentum gas from halos. Back.

⁹ In the updated z ≤ 1 metallicity analysis of Wotta et al. (2016), the statistical evidence for a bimodality is strongest for a subsample restricted to partial LLSs, with 16.2 ≤ logN_HI ≤ 17.2. Back.