2. CHARACTERISTIC PHYSICAL PARAMETERS

Gas depletion time-scale τ_g. The ratio between M_g and SFR, τ_g, can be measured directly. The mass of gas and the SFR are correlated as given by the so-called Kennicutt-Schmidt relation (Schmidt, 1959; Kennicutt, 1998), which is usually formulated in terms of the gas surface density, Σ_g, and the SFR surface density, Σ_SFR,

(6)

so that

(7)

Kennicutt & Evans (2012) give A and N for disk-averaged galaxies, which lead to τ_g from 3 to 0.5 Gyr for gas surface densities between 10 and 1000 M_⊙ pc⁻², typical of star-forming galaxies. Similar τ_g are obtained when considering spatially resolved measurements with sub-kpc resolution; see Fig. 1, adapted from Bigiel et al. (2008). It shows the lines of constant τ_g, and how the observations in the range of interests are close to the τ_g = 1 Gyr line.

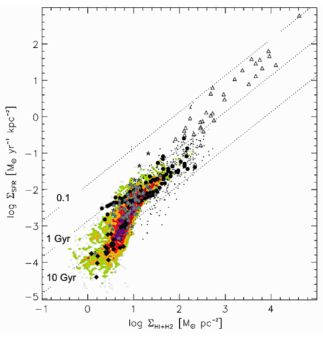Figure 1. Kennicutt-Schmidt relation at sub-kpc scales, i.e., SFR surface density versus gas surface density (labeled in the plot as ΣHI+H2 = Σg). The slanted dotted lines represent the expected relation for constant values of τg of 0.1, 1, and 10 Gyr. They encompass the observed data points. Adapted from Bigiel et al. (2008, their Fig. 15).

The Kennicutt-Schmidt law provides an empirical recipe linking SF with its fuel, and it has become central to the current numerical simulations of galaxy formation (e.g., Schaye & Dalla Vecchia, 2008; Dalla Vecchia & Schaye, 2008; Dalla Vecchia & Schaye, 2012). Therefore, the relation has deserved much attention in the literature, rendering depletion time-scales in the range of the above values (see Filho et al. 2016, and references therein).

Observations suggest that τ_g decreases with increasing redshift, so that it goes from 0.5 to 2 Gyr for galaxies in the redshift range between 2 and 0 (e.g., Genzel et al., 2010; Gnedin et al., 2014). This is consistent with the theoretical expectation that τ_g scales with the instantaneous Hubble time, t_H, as τ_g ≃ 0.17 t_H, so that at any time τ_g≪ t_H (Dekel et al., 2013).

Mass loading factor η. Stellar feedback is an essential ingredient of the current galaxy formation scenario since is it partly controls the predicted number of low-mass galaxies. Thus, its tuning allows us to reproduce the observed galaxy mass function (e.g., Silk & Mamon, 2012; Vogelsberger et al., 2014; Schaye et al., 2015. The mass loading factor quantifies the importance of this stellar feedback (Eq. [4]). Using the toy model, it is easy to argue that w should increase with decreasing stellar mass M_⁎, so that for low-mass galaxies,

(8)

In the stationary state, the metallicity of the gas that forms stars, Z, is independent of SFR and M_g. Z only depends on parameters characteristic of the stellar population, and on η, explicitly,

(9)

with Z_in the metallicity of the accreted gas, and y the stellar yield (the mass of ejected metals per unit mass locked into stars). Galaxies follow a well known mass-metallicity relation (MZR; see, e.g., Skillman et al., 1989; Tremonti et al., 2004) which, according to Eq. (9), can only be due to the dependence of η on M_⁎ since y and R are universals given the initial mass function (IMF). Moreover, for η to modify Z in a substantial way, Eq. (8) must be satisfied.

The fact that η varies with M_⁎ reaching large values for low-mass galaxies is found both in numerical simulations and in observational works. In order to reproduce the MZR, Peeples & Shankar (2011); Davé et al. (2012), and Dayal et al. (2013) use η varying from 1 to 6 when M_⁎ goes from 10¹¹ to 10⁹ M_⊙. The numerical simulations by Shen et al. (2012) lead to η between 1 and 10 for M_⁎ from 2 × 10¹¹ to 10⁹ M_⊙. In the cases modeled by Christensen et al. (2016), it goes from 0.5 to 50 for galaxies with virial masses from 10¹² to 2 × 10⁹ M_⊙. The numerical simulations carried out by Davé et al. (2013) assume η to be proportional to M_⁎^−1/3, with an even steeper dependence at low masses. The numerical simulations of giant star-forming clumps in gas-rich galaxies by Bournaud et al. (2014) render an effective η exceeding 2. Thompson & Krumholz (2016) model supersonic-turbulence driven outflows, and infer w ranging from 10⁻³ to 10. Observations of Mg II absorption around massive galaxies with M_⁎ ∼ 10¹¹ M_⊙ are used by Bordoloi et al. (2014) to set a conservative lower limit to η, which has to be larger then 0.24. Mass loading factors observed at high redshift generally refer to massive objects (M_⁎ > 10¹⁰ M_⊙), and turn out to be between 0.5 and 2 (Newman et al., 2012; Martin et al., 2012). It is not uncommon to infer factors up to 10 in local dwarfs (Martin, 21999; Veilleux et al., 2005). An extreme case is presented by Olmo-García et al., 2016, where faint multiple components in the wings of Hα are interpreted as produced by SN driven outflows with η often larger than 20.

Returned fraction R. Once the IMF is set, the stellar mass returned to the ISM is provided by stellar evolution models. 10 Gyr after the starburst, R is typically in the range between 0.2 and 0.3 when a Salpeter IMF is adopted (e.g., Edmunds, 2005; Leitner & Kravtsov, 2011). It can reach 0.5 for a Kroupa IMF, that has more massive stars for the same total mass of the stellar population (e.g., Leitner & Kravtsov, 2011; Segers et al., 2016).