3. SUB-GRID PHYSICS

3.1. Star Formation and the ISM

A huge body of observations from UV through near-IR light traces the emission from stars. In order to make contact with these observations, models must attempt to compute how gas in galaxies turns into stars. The ISM is a complex place, with multiple gas phases co-existing at very different densities and temperatures (McKee & Ostriker 1977). Cosmological simulations of more than a single galaxy are still orders of magnitude away from capturing the spatial scales, temperatures, and densities where stars actually form. Moreover, physical processes that are not typically included or captured well in cosmological simulations, such as magnetic fields and turbulence, are thought to play important roles on the scales of dense molecular cloud cores and protostars (McKee & Ostriker 2007). However, advances in our theoretical understanding of star formation as well as better observational characterization of key scaling relations (see Kennicutt & Evans 2012, for a review) have enabled the development of empirical recipes that smooth over much of the small-scale complexity.

Stars are observed to form in the dense, cold, molecular phase of the ISM, and current observations support a (nearly) universal star formation efficiency in molecular gas, where about 1% of the gas is converted into stars per free fall time (Bigiel et al. 2008, Bigiel et al. 2011, Leroy et al. 2013, Krumholz et al. 2012). Thus the ability to track where molecular gas forms should lead to a more physical approach to modeling star formation. The ISM is observed to become H₂-dominated at ∼ 1–100 atoms cm⁻³. Because gravitational instability is thought to be one of the driving forces in the formation of GMC (Dobbs et al. 2014), simply requiring a density threshold for star formation of a few atoms cm⁻³ may be a good first approximation. However, this also requires high enough resolution (≲ 100 pc) to attain these densities, which is currently achievable only in zoom simulations.

In more detail, H₂ formation is catalyzed by dust, and destroyed by Lyman-Werner radiation, so one would expect that H₂ production is thus roughly proportional to metallicity, while destruction depends on the ability to self-shield against interstellar radiation. Some zoom simulations now include a simplified phenomenological treatment of chemical networks and H₂ dust- and self-shielding (Gnedin et al. 2009, Christensen et al. 2012). Fitting functions that attempt to capture the essence of H₂ formation and dissociation and the resulting dependence of H₂ fraction f_H2 on gas density, metallicity, and local UV background have been presented based on these and on idealized (non-cosmological) disk simulations and analytic models (Krumholz et al. 2009, McKee & Krumholz 2010, Gnedin & Kravtsov 2011, Gnedin & Draine 2014).

An alternative approach for partioning gas into H i and H₂ is to use the empirical relationship between f_H2 and the disk mid-plane pressure, pointed out by Blitz & Rosolowsky (2004, BR). They found that the molecular fraction R_mol ≡ Σ_H2 / Σ_HI was correlated with the disk hydrostatic mid-plane pressure P: R_mol = (P / P₀)^α_BR, where P₀ and α_BR are free parameters that are obtained from a fit to the observational data. The hydrostatic pressure as a function of radius in the disk can be estimated based on the cold gas surface density, the stellar surface density, and the ratio of the vertical velocity dispersions of the gas and stars (Elmegreen 1989). This approach can be used to estimate f_H2 either self-consistently (see below) or in post-processing in numerical simulations or SAMs (Duffy et al. 2012, Obreschkow et al. 2009).

3.1.1. Numerical Implementation. The basic recipe for star formation in many cosmological simulations has not changed markedly from the pioneering work of (Katz 1992). Gas that is dense and converging is assigned a SFR based on a Schmidt (1959) law, namely

(3)

where the last proportionality arises because the local free-fall time t_ff∝ ρ^−0.5. The free parameter є_∗ is typically calibrated to match the amplitude of the observed (Kennicutt 1998) relation in simulations of idealized, isolated disks. Long-term SF histories are generally insensitive to є_∗ within reasonable choices (Katz et al. 1996, Schaye et al. 2010), because as discussed later, globally, SF is driven primarily by gas accretion, and over cosmological timescales is not limited by the rate of conversion of gas into stars in the ISM. A somewhat different approach was proposed by Schaye & Dalla Vecchia (2008): they analytically recast the Kennicutt-Schmidt relation as a function of pressure rather than density, assuming a self-gravitating disk.

Stars are generally only allowed to form when the density exceeds some critical value, the choice of which is another free parameter. Springel & Hernquist (2003) incorporated a density threshold based on where the Jeans mass became lower than the particle mass, at which point a sub-grid ISM model is required; this value turned out to be ≈ 0.1 cm⁻³ for typical mass resolutions adopted in cosmological volumes at the time.

This simple SF prescription applied to individual disk galaxies was found to quickly collapse gas down to the (artificial) Jeans scale in the simulations, which produced highly clumpy disks that looked nothing like local grand-design spirals. The solution, introduced in cosmological runs by Springel & Hernquist (2003) was to artificially overpressurize the ISM, by implementing a sub-grid ISM model based on McKee & Ostriker (1977) that tracked the balance between SN energy input and cooling within a multi-phase ISM. The temperature of the ISM gas (defined as gas above the SF threshold density) is then raised up to as high as 10⁶ K. Robertson et al. (2004) extended this model to an arbitrary ISM effective equation of state, and showed that with appropriate overpressurization, this approach can reproduce smooth, stable, gas-rich spirals as observed today. Ironically, as we discuss further in Section 4.2.1, it turns out that simulations with no or minimal ISM pressure (Ceverino et al. 2010, Ceverino et al. 2014) do well at reproducing the clumpy disks that are now known to be common at high redshift (z ∼ 2; Genzel et al. 2011), though simulations with pressurization can also reproduce these (Genel et al 2012b).

It is clear that real stars do not form at densities of ∼ 0.1 atoms cm⁻³. Moreover, since the Kennicutt relation is only observed to hold when the ISM is averaged over scales of 0.5−1 kpc, once simulations resolve smaller scales, it becomes dubious to use a SF prescription that is calibrated to match this relation. Thus much recent effort has gone into incorporating more realistic treatments of the ISM into cosmological simulations. High-resolution zoom simulations that simply adopt a higher star formation threshold ( ∼ 5 atoms cm⁻³) and efficient stellar-driven winds (see Section 4.2.1 for further discussion) show marked improvement in their ability to produce realistic disks (e.g. Governato et al. 2007, Guedes et al. 2011). Other simulators (e.g. Kuhlen et al. 2012, Agertz & Kravtsov 2014) have incorporated sub-grid recipes to compute the density of molecular hydrogen ρ_H2 and then use that in an equation similar to Eqn. 3 in place of ρ_gas — no arbitrary density threshold need then be applied.

An exciting development is that cosmological zoom simulations are starting to be able to resolve the Jeans mass/length of gas, corresponding to the scale of molecular cloud complexes, allowing more direct modeling of the multi-phase ISM, (e.g. the FIRE simulations, Hopkins et al. 2013a). Concurrently, ISM simulations including detailed treatments of non-equilibrium chemistry and turbulence are pushing outwards in scale to start “bridging the gap” with the cosmological runs (e.g. Walch et al. 2011, Mac Low & Glover 2012). Continuing interactions between the galaxy formation and ISM/star formation communities will soon allow us to place our sub-grid recipes on a more secure physical foundation.

3.1.2. Implementation in Semi-Analytic Models. The usual approach to modeling star formation in SAMs is very similar to the approach used in numerical hydro simulations, described above. Gas that has “cooled” according to the cooling model described in Section 2.3.2 loses its pressure support and collapses further, until it is supported by its angular momentum, forming a disk. The initial angular momentum of the halo gas can then be used to estimate the radial size of the disk, as described in Section 4.2.4. Some SAMs track the radial structure of the disk in cylindrically symmetric annuli (Kauffmann 1996, Avila-Reese et al. 1998, Dutton & van den Bosch 2009, Fu et al. 2010), while most models assume the disk radial surface density distribution to be an exponential, as is generally the case in observed disk galaxies.

Different SAMs use different but roughly physically equivalent variants of Eqn. 3. Early SAMs typically used an expression of the form

where _∗ is the total star formation rate in the galaxy, m_cold is the total cold gas mass in the galaxy, τ_∗ is a characteristic timescale for star formation, and є_∗ is a parameter representing the global star formation efficiency. The SF timescale is often assumed to scale with the dynamical time of the dark matter halo, τ_∗ ∝ τ_dyn ∝ r_h / V_h, where r_h is the characteristic halo radius and V_h is the characteristic halo circular velocity. However, it was quickly realized that a SF law of this form could not reproduce the observed trend of increasing cold gas fractions with decreasing stellar mass in the low redshift universe. Thus, modelers either introduced a SF threshold, such that only the fraction of the cold gas above this threshold was eligible to participate in star formation, or made τ_∗ an explicit function of halo properties, e.g. of V_h (Cole et al. 2000), such that the star formation timescale is made longer in lower mass galaxies.

Models that track disk structure in more detail are able to use empirical laws that are closer to what is actually observed. For example, Somerville et al. (2008) adopted a “Kennicutt”-like expression, where the star formation rate surface density of the disk is calculated according to Σ_SFR = A_SFΣ_gas^N_SF for Σ_gas > Σ_crit (and zero otherwise). The parameters A_SF and N_SF are taken directly from observations (e.g. Kennicutt 1998), and Σ_crit is treated as a free parameter. A similar approach, but with a radius and circular velocity dependent Σ_crit based on the Toomre condition for gravitational instability, is adopted in the MPA SAMs (e.g. Kauffmann et al. 1999, Croton et al. 2006, Guo et al. 2011).

Several groups have recently developed SAMs that attempt to track atomic and molecular gas separately (Fu et al. 2010, Lagos et al. 2011b, Popping et al. 2014b, Somerville et al. 2014). Various recipes for H₂-formation, either employing the metallicity-based fitting functions of Krumholz et al. (2009)) and Gnedin & Kravtsov (2011), or alternatively the empirical pressure-based recipe from Blitz & Rosolowsky (2004), have been implemented in these SAMs. Again, the computed density of H₂ may then be used in an empirically calibrated SF law with no need to assume a density threshold — essentially removing all free parameters from the SF recipe (within the observational uncertainties on the slope and normalization of the relationship between Σ_SFR and Σ_H2). Overall, it appears that the main predictions of SAMs, especially for stellar properties of galaxies, are quite insensitive to the details of the gas partitioning recipe (Fu et al. 2010, Lagos et al. 2011b, Popping et al. 2014b, Somerville et al. 2014, Berry et al. 2014).

It is well known that galaxy interactions and mergers can trigger starbursts with enhanced star formation efficiency (SFE), and most SAMs implement a “burst mode” of star formation in galaxies that have experienced a recent merger. Studies based on hydrodynamic simulations of binary galaxy mergers have shown that the enhancement in the SFE above that in an isolated galaxy is a fairly strong function of the mass ratio of the merger. Many SAMs implement the fitting function introduced by Cox et al. (2008), who parameterized the burst efficiency as e_burst = e_{burst, 0} µ^γ, where µ is the merger mass ratio, and e_burst is defined as the fraction of the total gas reservoir that is consumed in the burst.

Subsequent studies have shown that e_burst and the burst timescale also depend on the implementation of stellar feedback and the treatment of the ISM (Cox et al. 2008, Robertson et al. 2006b). Hopkins et al. (2009a) found that the burst efficiency depended strongly on the cold gas fraction in the progenitors, with lower burst efficiencies in mergers with higher progenitor gas fractions. However, Moster et al. (2011) did not find a strong correlation with the progenitor cold gas fraction when they including a hot halo in the merger progenitors. Although there have been numerous studies of star formation enhancement in mergers using numerical hydrodynamic simulations of binary mergers (e.g. Mihos & Hernquist 1996, Springel 2000, Cox et al. 2006, Cox et al. 2008), these simulations are not in a cosmological context, and therefore must assume idealized initial conditions. Furthermore, most have not included cosmological accretion or cooling from a hot gas halo. To our knowledge, there has not been a systematic exploration of the enhancement of star formation activity in mergers using cosmologically-situated hydrodynamic simulations.

SAMs predict that burst-mode star formation makes a relatively minor contribution to the overall global star-formation rate density at any epoch (e.g. Baugh et al. 2005, Somerville et al. 2008), in agreement with observations (Rodighiero et al. 2011, Schreiber et al. 2014) and cosmological hydro simulations (Murali et al. 2002, Kereš et al. 2005). However, merger-triggered bursts may be important for producing certain populations such as ultra-luminous infrared galaxies (ULIRGS) and high-redshift sub-mm detected galaxies (Niemi et al. 2012, Hayward et al. 2013), in agreement with observations that suggest a strong connection between major mergers and starbursts (e.g. Sanders & Mirabel 1006, Kormendy et al. 2009).

3.2. Black Hole Growth

The first “seed” black holes may have been left behind after the explosion of massive stars formed out of primordial gas in the early universe. These “Pop III” seed BH are expected to have masses of ∼ 100 M_⊙; however, such seeds cannot grow into the 10⁹ M_⊙ black holes required to power observed quasars at z ∼ 6−7 if their growth is Eddington-limited. Recently, several mechanisms for creating more massive seed BH (10⁴ – 10⁶ M_⊙) have been proposed (see Volonteri 2010, for a review). However, in cosmological simulations, the usual approach is to place seed BH by hand in halos above a critical mass (M_h ≳ 10¹⁰ – 10¹¹ M_⊙). In some cases, seeds of a fixed mass are used, in others, the seed mass is chosen to place the BH on the local M_BH − σ relation. The results that we will discuss here are generally insensitive to the details of the seeding procedure.

One must then calculate how rapidly these seed BH will accrete gas and grow in mass. The currently predominant model relies on the idea that black hole growth is limited by Bondi accretion of mass within the sphere of influence (Bondi 1952), given by

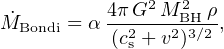(4)

where M_BH is the mass of the BH, c_s is the sound speed of the gas, v is the bulk velocity of the BH relative to the gas, ρ is the density of the gas, and α is a boost parameter included because models typically lack the spatial resolution to resolve the Bondi radius (Booth & Schaye 2009, Johansson et al. 2009a). Early models took α to be constant (typically ∼ 100), but some simulators make α a function of density (e.g. Booth & Schaye 2009) and some recent simulations resolve the Bondi radius so can adopt α = 1. Typically, the accretion rate is capped at the Eddington rate. As galaxies merge, their BHs are assumed to merge when they come within some distance of each other, typically a softening length (thereby ignoring GR timescales for BH inspiral).

The Bondi accretion model predicts fairly low accretion rates when galaxies are undisturbed, but when strong torques drive gas towards the nucleus as in a major merger, accretion rates can be boosted to levels sufficient to power quasars (Springel et al. 2005b, Di Matteo et al. 2005). This is consistent with the observation that local ULIRGs, which are mostly major mergers, also show strong AGN activity (Sanders & Mirabel 1996). In one paradigm, low accretion rates (≲ 0.01 _Edd, where _Edd is the Eddington rate) are associated with radiatively inefficient accretion, as in an Advection Dominated Accretion Flow (Narayan & Yi 1994, Blandford & Begelman 1999). In this case, most of the energy is advected into the BH and little emerges as radiation. BH powered at higher accretion rates are radiatively efficient and give rise to the population of observed X-ray, UV, and optically luminous quasars and AGN.

The assumption of Bondi accretion requires accompanying strong feedback to obtain BHs that follow the M_BH − σ relation, as this simple argument demonstrates (Anglés-Alcázar et al. 2013a). Consider two BHs of mass M_a and M_b. If they grow according to the general prescription _BH = D(t)M_BH^p, then

(5)

It is easy to show that the two masses will diverge if p > 1, and they will converge if p < 1. For Bondi accretion p = 2; hence for BHs to converge onto an M_BH − σ relation, some strongly self-regulating feedback process must counteract Bondi accretion and make p effectively less than unity. We will discuss possible feedback processes in Section 3.3.3, but in general such tuned self-regulation is not so straightforward to arrange, for the usual reason that outward energetic processes tend to escape through paths of least resistence whereas inflows typically arrive through the dense, harder-to-disrupt gas.

It is worth emphasizing that the widely used Bondi model implicitly assumes that the accreting gas has negligible angular momentum, which is unlikely to be a good assumption in general. Recently, the problem of dissipating angular momentum to enable BH accretion has received more attention in the cosmological milieu. Hopkins & Quataert (Hopkins:2010c,Hopkins:2011d) studied angular momentum transport in disks with non-axisymmetric perturbations both analytically and in simulations, showing that such secular processes can significantly fuel BH growth, as also suggested by Bournaud et al. (2011) and Gabor & Bournaud (2013). Implementing this analytic work into zooms and cosmological runs, Anglés-Alcázar et al. (2013a) and Anglés-Alcázar et al. (2013b) showed that this torque-limited accretion behaves qualitatively differently than Bondi accretion, since in the Hopkins & Quataert (2011) model, the exponent of BH growth is p = 1/6. Hence while this model also must incorporate feedback, such feedback does not have to strongly couple to the inflow in order to achieve self-regulation.

Black hole accretion in SAMs is of necessity more schematic. In one of the first semi-analytic models that incorporated BH growth in the framework of a cosmological model of galaxy formation, Kauffmann & Haehnelt (2000) assumed that all BH growth is triggered by major mergers. Following such an event, they assumed that some fraction of the cold gas was accreted by the BH, with this fraction being a function of the halo circular velocity. A similar recipe is incorporated into the later generations of MPA-SAMs (e.g. Croton et al. 2006, De Lucia & Blaizot 2007, Guo et al. 2011, Henriques et al. 2013). Other SAMs additionally trigger accretion following minor mergers and disk instabilities (Somerville et al. 2008, Hirschmann et al. 2012b, Bower et al. 2006). Some models allow an additional growth channel through a “Bondi-like” accretion from the hot halo (Somerville et al. 2008, Fanidakis et al. 2011). In the Santa Cruz SAMs (Somerville et al. 2008), black hole growth is parameterized based on the results of hydrodynamic binary merger simulations (Cox et al. 2006, Cox et al. 2008, Robertson et al. 2006b) as characterized by (Hopkins et al. 2005b). In this model, rapid black hole accretion is triggered following a major or minor merger. The BH accretes at the Eddington rate until the BH reaches a critical mass, where the energy being radiatied is sufficient to halt further accretion. The accretion rate then declines in a power-law “blow out” phase until the BH switches off (Hopkins et al. 2005a).

All SAMs and numerical cosmological hydrodynamic simulations that explicitly include BH growth use the local M_BH − σ or M_BH − M_spheroid relation to calibrate the free parameters in the BH accretion recipes. A wide variety of BH growth recipes appear to be able to successfully reproduce this relationship.

3.3. Feedback Processes

Feedback can be divided into two general classes, preventive and ejective. Preventive feedback retards star formation by stopping gas from accreting into the ISM, while ejective feedback describes processes that remove the gas from the ISM after it has been accreted. Current wisdom suggests that preventive feedback dominates when the majority of halo gas is near the halo’s virial temperature (as in very small dwarfs or massive galaxies), while ejective feedback dominates when most of the halo’s gas is well below its virial temperature (as in typical star-forming galaxies). However, individual physical processes can potentially act in both ejective and preventive ways.

3.3.1. Squelching: Photoionization Suppression. Photons above 13.6 eV that ionize hydrogen typically add an ∼ eV-scale amount of latent heat, corresponding to a temperature increase of ∼ 10⁴ K. Hence the post-reionization optically-thin IGM has a temperature around this value, which means that gas in halos whose virial temperatures are comparable to 10⁴ K will be unable to cool their gas. This temperature corresponds to a halo mass of ∼ 10⁸ M_⊙, implying that photoionization will strongly reduce the baryon content and hence suppress galaxy formation in halos below this mass. This suppression has sometimes been called squelching (Somerville 2002).

Squelching can have a residual impact on halos much larger than 10⁸ M_⊙, since they are hierarchically assembled in part from squelched halos. Gnedin (2000) showed that the characteristic mass below which halos contain substantially less than their fair share of baryons is well represented by a filtering scale that smooths the baryonic perturbations. Hence one can define a filtering mass, which describes the halo mass that on average contains half the cosmic fraction of baryons.

The filtering mass depends on the intricate interplay between photoionization, cooling, and hierarchical growth, which is challenging to model. Early work suggested a roughly constant circular velocity below which baryon accretion is suppressed, of around 30−50 km/s (e.g. Thoul & Weinberg 1996, Quinn et al. 1996). If extrapolated to today, this would imply halos up to several times 10¹⁰ M_⊙ would be significantly suppressed in baryon content (Gnedin 2000). More recent simulations by Okamoto et al. (2008) found a smaller filtering mass scale, M_F ∼ 4 × 10⁹ M_⊙ today, but these simulations still assumed ionization equilibrium, did not include metal line cooling, and adopted a uniform meta-galactic ionizing background. Observations of late-type dwarfs with circular velocities ≲ 42 km/s suggest that their baryon content is much smaller than expected from scaling relations based on larger galaxies (Kormendy & Freeman 2014), thus providing direct constraints on the filtering mass.

An additional complication can arise when galactic outflows are included along with squelching, as the two can combine to produce an “amplification of suppression” that is stronger than the product of the individual effects (Pawlik & Schaye 2009, Finlator et al. 2012). The magnitude of the effect depends on the outflow model implemented, but can be up to a 60% amplification during the EoR. Unfortunately, the high expense of these calculations that include radiative transfer while resolving very small halos prohibits their evolution down to z = 0; hence it is not clear how significant this effect is at later epochs.

In semi-analytic models, photoionization squelching is generally implemented by assuming that reionization occurs instantaneously throughout the Universe, at a fixed input redshift. At all later times, the gas that is allowed to accrete into halos is reduced by a factor f_coll(M_h, z). This function is parameterized based on the results of numerical hydrodynamic simulations, and is expressed as a function of the filtering mass (Gnedin 2000, Kravtsov et al. 2004, Okamoto et al. 2008).

3.3.2. Star Formation Feedback. Stars, massive ones in particular, deposit copious amounts of energy and momentum into the ISM during their life and in death. Stellar feedback is invoked to explain two kinds of inefficiencies in galaxies: 1) The efficiency of the conversion of gas into stars within GMC’s is puzzlingly low, only about 1% per free fall time (Krumholz et al. 2012; 2) the stellar and baryon fraction within galactic-sized halos is much less than the universal value, ranging from a few to twenty percent (Moster et al. 2010b, Behroozi et al. 2010). The first inefficiency has been ascribed to turbulence generated by stars and SNe within GMCs (Krumholz et al. 2012, and references therein). For purposes of cosmological simulations, since observations suggest that this efficiency is nearly universal, this can largely be folded into the normalization of the star formation recipe.

The second inefficiency is generally ascribed to large-scale galactic outflows powered by massive stars and SNae. Signatures of such outflows, with mass loss rates likely of the same order as the star formation rate or larger, are ubiquitously observed in star forming galaxies (Veilleux et al. 2005). Modeling galactic outflows has therefore become a central challenge for recent simulations.

Early work attempted to model stellar feedback via the deposition of thermal energy from SNae in the surrounding gas (e.g. Katz et al. 1996). It was quickly realized that this had almost no effect, because the short cooling times meant that the energy was radiated away very quickly, adding negligible ISM pressure, let alone driving an outflow. Since then, most cosmological models have adopted some sub-grid prescription to enable effective ejective feedback that typically involves either implementing ad hoc “tricks”, such as turning off cooling for some time or super-heating the gas, that attempt to mimic the ISM processes that allow stellar-driven winds to develop in real galaxies, or else implementing outflows via kinetic energy injection.

A variant on the ISM heating model called “blast wave” feedback was developed by Stinson et al. (2006) and has been extensively used in Gasoline and RAMSES (Bournaud et al. 2010). Here, after the gas is heated, radiative cooling is shut off for the lifetime of the SN-driven blastwave as predicted by a spherical Sedov solution. This enables the gas to “feel” the higher pressure and develop a coherent large-scale outflow. While successful in many regards, this model still predicted too much early star formation, so Stinson et al. (2013) added “early stellar feedback” intended to mimic the energy input from young stellar winds and radiation.

Another variant of a purely thermal stellar feedback model was proposed by Dalla Vecchia & Schaye (2012) and implemented in the EAGLE simulations (Schaye et al. 2014). Instead of turning off cooling, the trick for preventing the energy from immediately cooling away involves making the energy deposition stochastic. The mean amount of energy injected per mass of stars formed is set by stellar population models and supernova energetics. The temperature jump of particles receiving a boost is specified (ΔT = 10^7.5 K, typically), and a parameter f_th determines the probability that a given SPH particle in the vicinity of a star-forming particle will get heated. Hence the gas is heated to much higher temperatures than would be the case if the same amount of energy were continuously added to all of the SPH neighbors, increasing the cooling time and mitigating energy losses. The overall efficiency of the feedback can be adjusted by varying f_th. Schaye et al. (2014) made f_th a function of the local gas metallicity and density, as they found that this most successfully reproduced the observed SMF and galaxy sizes.

A popular approach introduced by Navarro & White (1993) and implemented into Gadget-2 by Springel & Hernquist (2003) is to simulate outflows by giving gas “kicks”, rather than trying to overpressurize ISM gas by adding thermal energy. Such kinetic outflows are less directly tied to the physics generating outflows, but enable greater control over outflow parameters in order to both mimic observed outflows more closely and assess the impact of varying the outflow parameters. In such models, hydrodynamics is sometimes shut off (“decoupled”) for some period of time to mimic the collective power of supernovae blowing a chimney through the ISM; it is unclear whether this provides a more physical description of outflow propagation through the ISM, but it generally does result in better resolution convergence (Dalla Vecchia & Schaye 2008). These models are parameterized by a mass loading factor η ≡ _out / _∗ and a wind velocity v_wind, which together determine how many particles to kick and how hard to kick them. Springel & Hernquist (2003) assumed a constant mass loading factor and constant wind velocity, and showed that this yielded a cosmic star formation history in much better agreement than a model without outflows. Oppenheimer & Davé (2006) showed that adopting scalings motivated by analytic “momentum-driven” wind models (Murray et al.2005) produced better agreement with many galaxy and IGM properties including the galaxy mass-metallicity relation, the enrichment history of the IGM, and the galaxy stellar mass function (see also Oppenheimer & Davé 2008, Finlator & Davé 2008, Davé et al. 2011b, Davé et al. 2013). For momentum-driven winds, the mass loading factor scales as η ∝ σ⁻¹, and the wind velocity scales as v_wind ∝ σ, where σ is the velocity dispersion of the galaxy. The Illustris simulations (Vogelsberger et al. 2014a) also employ kinetic winds by creating and launching decoupled wind particles, and rejoining them back into the gas mesh after recoupling. They adopt scalings expected for “energy-driven” winds, namely η ∝ σ⁻².

Most semi-analytic models parameterize star formation feedback in a similar manner, based on the approach introduced in White & Frenk (1991) and (Kauffmann et al. (1993). In each timestep, the SAM computes the rate at which cold gas is ejected from the disk by a wind:

where _∗ is the star formation rate in the galaxy, V_c is the circular velocity of the galaxy, V₀ is an arbitrary normalization parameter, and є_w and α_w are treated as tunable free parameters. For α_w = 1 or α_w = 2, this is equivalent to the “momentum driven” or “energy driven” wind scalings discussed above. One must then decide what happens to the ejected gas, and here different modelers diverge more widely. Some fraction of the ejected gas may escape the dark matter halo, and may be tracked in an “ejected” reservoir from which it is allowed to accrete into the halo again over a longer timescale. Otherwise, the ejected gas is added to the halo hot gas reservoir. SAMs generally implement some sort of model, of varying complexity, to arrange that the fraction of ejected gas that escapes the halo is larger at lower halo V_h, and assymptotes to unity above V_h ≃ 120-150 km/s (or a halo mass of a few × 10¹² M_⊙).

3.3.3. AGN Feedback. Observational phenomena associated with accreting black holes include electromagnetic radiation, relativistic jets, and less-collimated non-relativistic outflows (Krolik 1999). There are several different physical mechanisms whereby the large amounts of energy and momentum produced by AGN can couple with the gas in and around galaxies, possibly regulating the growth of the black hole itself, and potentially suppressing cooling and star formation on galactic scales. At the most basic level, AGN can heat gas up (thermal feedback), drive winds that eject gas (kinetic feedback), and ionize or photo-dissociate gas (radiative feedback). The main heating mechanisms are Compton, photo-ionization, and photo-electric heating. Radiation may also drive winds via pressure on spectral lines, free electrons, or dust. These winds may originate in the torus or accretion structure near the black hole, the broad line region (BLR), larger nuclear scales ( ∼ kpc), or all of the above. Winds arising on “small” (BLR/accretion disk) scales may drive galaxy-scale winds by shocking and sweeping up ISM gas — or they may simply vent out of the galaxy without ejecting much mass. In addition, highly relativistic giant radio jets may heat the intra-cluster medium through bubbles, weak shocks, and sound waves (McNamara & Nulsen 2007, Fabian 2012).

Focussing first on the processes associated with the radiatively efficient (“radiative mode”, sometimes called “quasar mode” or “bright mode”) of BH growth, one of the major dynamical questions is whether AGN-driven winds are primarily “energy driven” or “momentum driven”. As in the case of stellar driven winds, the question is how quickly and efficiently is the thermal energy generated when the wind shocks the surrounding gas radiated away. Momentum cannot, of course, be radiated away, and so if most of the thermal energy is quickly dissipated, we term the wind “momentum driven”. If radiative losses are negligible, we term it “energy driven”. Clearly real winds may often be somewhere in between. The significance of this distinction is that the momentum flux of swept-up material in an energy-conserving outflow is “boosted” due to work done by the hot shocked gas (an effect familiar from the Sedov-Taylor phase in supernova remnants).

It has been argued that in the dense cold gas that must surround rapidly accreting black holes, cooling times are short and winds must be predominantly momentum-driven (King 2005, Ostriker et al. 2010, Debuhr et al. 2011). However, observations of AGN-driven outflows suggest “boost” factors of 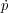/ 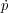_rad ∼ 2–30 (e.g. Sturm et al. 2011, Moe et al. 2009), with an average probably around 10, where 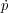_rad = L_AGN / c is the radiative momentum flux output by the AGN. Faucher-Giguère & Quataert (2012) argued recently based on analytic calculations that AGN-driven outflows are likely to be largely energy-conserving in many situations relevant to observed systems, particularly for “fast” (v_w ∼ 10,000-30,000 km/s) winds.

One of the earliest three dimensional simulations of AGN feedback in galaxies was presented in Springel et al. (2005b) and Di Matteo et al. (2005). Here, the BH accretion rate was modelled using the Bondi approach outlined above, and the resulting bolometric luminosity was assumed to be proportional to the BH accretion rate. A fixed fraction of the bolometric luminosity was deposited into the neighboring gas particles as thermal energy. These simulations did not use cosmological initial conditions, but considered binary mergers of idealized disk galaxies without hot gas halos. This work showed that deposition of about 5% of the bolometric luminosity was able to drive strong outflows that eventually halted further accretion onto the BH and also removed nearly all cold gas from the galaxy, resulting in quenching of star formation (Springel et al. 2005a). Furthermore, the models produced self-regulated BH growth, leading to a tight M_BH − σ relationship in agreement with the observed one. A similar approach has been used in a large number of subsequent studies. Although these studies, taken at face value, suggest that purely energy driven winds can regulate BH growth and drive large-scale outflows, it is likely that radiative losses were artificially suppressed due to the highly pressurized ISM model adopted in these simulations.

Moreover, these simulations neglected the expected momentum deposition. Several recent works have implemented momentum-driven winds in hydrodynamic simulations via radiation pressure on dust (Debuhr et al. 2010, Debuhr et al. 2011) and via BLR winds (Choi et al. 2012, Choi et al. 2014a) and found that these winds can play a significant role in modulating the growth of the black hole and the galaxy. The star formation remains quenched over a much longer timescale in the simulations that include momentum-feedback, because the density of hot gas near the center of the halos is significantly reduced (Choi et al. 2014b).

The other important class of feedback processes is connected with highly collimated jets of relativistic particles (“jet mode” or “radio mode”; see the recent reviews by Fabian 2012 and Heckman & Best 2014). The kinetic energy in these jets can exceed the total bolometric luminosity of the AGN by several orders of magnitude. While jets may be observed at many wavelengths, there is a class of sources detected at radio wavelengths that do not exhibit the classical signatures of “radiatively efficient” AGN — no UV, X-ray, or IR excess, and no highly ionized emission lines. Optically, these objects resemble normal massive early type galaxies. They are associated with radiatively inefficient accretion, and with extremely low accretion rates onto the central BH. The radio jets are observed to correspond, in many cases, with “bubbles” visible in X-ray images, regions filled with hot plasma presumably heated by shocks from the jet’s interaction with the ICM. Studies of the bubble energetics have shown that there is easily enough energy deposited in the ICM to offset cooling; in fact, in groups and low-mass clusters the energy probably exceeds the requirements for balancing cooling by up to an order of magnitude. Radio galaxies are common in massive early type galaxies in groups and clusters, and bubbles and/or radio sources are seen in 95% of “cool core” clusters (clusters with short central cooling times).

Once again, the energetics are such that one expects this “jet mode” feedback to have a significant impact on galaxy formation, but many details of the physics remain unclear. The main puzzle is how such highly columnated bi-polar jets can nearly isotropically heat a large volume of intragroup or cluster gas (Vernaleo & Reynolds 2006). The bubbles provide an important clue — these bubbles rise buoyantly in the hot atmosphere, reaching fairly large radii. Heating may occur via turbulent mixing of bubbles with the ICM (Scannapieco & Brüggen 2008), viscous dissipation of weak shocks (Ruszkowski et al. 2004), or cosmic ray heating (Sharma et al. 2009). Although some recent simulations that attempt to explicitly model jet heating in 3D have claimed greater success at averting the cooling flow problem (Gaspari et al. 2011, Li & Bryan 2014), all of these simulations neglect a cosmological formation history, with merging and accretion, as well as star formation and stellar feedback. A detailed physical understanding of how the jets couple to the surrounding hot gas and how effective they are in regulating cooling flows over long timescales remains lacking (see also Babul et al. 2013, Cielo et al. 2014).

Sijacki et al. (2007) were the first to attempt to include both the “radiative” and “jet” modes of AGN feedback in numerical cosmological simulations, albeit in a simplified way, necessitated by the relatively coarse numerical resolution. Above a critical black hole accretion rate ( ∼ 0.01 times the Eddington rate), the AGN was assumed to be radiatively efficient and a fraction of the AGN bolometric luminosity was deposited in the gas as thermal energy. Below the critical accretion rate, the AGN is assumed to be radiatively inefficient and to produce jets which inflate bubbles — however they do not directly simulate the jet. Instead they insert bubbles by hand, with energy and radius scaled to the black hole mass as motivated by analytic models for radio cocoon expansion.

Similar approaches have now been implemented in a few sets of cosmological simulations. The Illustris simulations, using the Arepo moving mesh code, also use the Bondi accretion model and a similar feedback scheme to that of Sijacki et al. (2007). In addition, the Illustris simulations include a simplified treatment of photo-ionization and photo-heating due to the AGN radiation field. A somewhat different approach is taken in the EAGLE (Schaye et al. 2014) and OWLS (Schaye et al. 2010) simulations — they adopt a variant of the “stochastic thermal feedback” model used for star formation feedback, described in Section 3.3.2, in which an average energy injection rate is given by E_BH ∝ _acc c², where _acc is the accretion rate onto the BH and c is the speed of light. The injected energy is stored by each BH until it can stochastically heat some minimum number of particles with a temperature increase ΔT. The value of ΔT may depend on resolution, and is higher than for the stellar feedback model ΔT ∼ 10^8.5–10⁹ K (Schaye et al. 2014). Other simulations do not explicitly follow black hole growth and associated feedback, but include heuristic “quenching” mechanisms based on surrogate galaxy or halo properties (Gabor et al. 2011, Gabor & Davé 2012).

A large number of groups have also implemented “radiative mode” AGN-driven winds and “jet mode” AGN heating in semi-analytic models. Although the details differ from model to model, there are a number of common elements that are widely adopted: 1) A distinction is made between black hole fueling via cold gas (which is typically assumed to be driven into the nucleus by mergers and/or disk instabilities; see Section 3.2), and hot gas which is generally assumed to accrete via a cooling flow. 2) BH accretion fueled by the merger/disk instability driven mode is associated with radiatively efficient accretion at a significant fraction of the Eddington rate; accretion fueled by hot gas is assumed to lead to very sub-Eddington, radiatively inefficient accretion associated with the “jet mode”. 3) The “jet mode” is assumed to be activated only in the presence of a quasi-hydrostatic hot halo, i.e. when the halo is predominantly accreting via the “hot mode” discussed earlier. 4) The “jet mode” is able to extract a certain fraction of the BH mass in the form of energy, which is used to offset cooling, or is assumed to be able to establish heating-cooling balance when the BH mass exceeds a critical value.

For example, in the Croton et al. (2006) model, the “jet mode” accretion rate is modeled as:

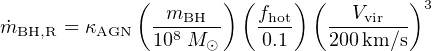where f_hot is the fraction of the total halo mass in the form of hot gas, m_BH is the mass of the black hole, and V_vir is the virial velocity of the halo. The cooling rate computed as described in Section 2.3.2 is offset by a heating term, such that the effective cooling rate is:

where L_AGN = є_{rad BH} c² with є_rad = 0.1 the conversion of accreted rest mass into energy. Other SAMs use similar scalings, some with more attempted explicit connection with the invoked physical processes and/or with observations (e.g. Somerville et al. 2008, Monaco et al. 2007), but these appear to produce similar results at z = 0, and even for the redshift evolution of massive galaxies (Fontanot et al. 2009).

In addition to “jet mode” feedback, some SAMs implement AGN-driven winds. Somerville et al. (2008) adopted momentum driven wind scalings associated with “radiative mode” AGN activity:

where є_wind represents the effective coupling efficiency, V_esc is the escape velocity of the galaxy, and _acc is the BH accretion rate in the radiatively efficient mode. See also Fontanot et al. (2006) for an alternate implementation of “radiative mode” wind feedback in SAMs.

Examples of SAMs that do not follow BH growth explicitly, but instead implement more heuristic halo-based quenching include Cattaneo et al. (2006) and Lu et al. (2011). In these models, cooling is simply switched off when the halo mass exceeds a critical value, which may depend on redshift.