How Galaxies Don't Form

2.1. Density Begets Density

Since I am going to contradict some widely held notions, it seems only fair to start by trashing my own favorite idea. Many of the properties of LSB galaxies (McGaugh 1992) suggested to me that they were basically stretched out, lower density versions of HSB galaxies. They also appear to be somewhat younger than HSB galaxies, suggesting a later collapse epoch (McGaugh & Bothun 1994).

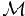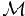It seems natural that the properties of dark halos might dictate the properties of the luminous galaxies they contain. In addition to a distribution of masses Mitalic _h which gives rise to the luminosity function, there could also be a distribution of scale sizes R_h which, at a given mass, gives rise to the distribution of disk scale lengths (or equivalently, the surface brightness distribution: McGaugh 1996). The mapping from ( Mitalic _h, R_h) to (L, h) need not be simple, but assuming it is forms an obvious starting point. In this picture (which I refer to as ``density begets density,'' or DD), HSB disks arise from large density fluctuations delta , and LSB disks from low delta (but not necessarily low mass).

DD makes several predictions beyond the data which motivated it (McGaugh & de Blok 1998a). One is that since HSB and LSB galaxies represent populations which arose from different characteristic delta , there should be a shift between the correlation function of the two. This prediction was confirmed (Mo et al. 1994).

In DD, LSB galaxies and their halos are stretched out versions of HSB systems. Two predictions follow about their dynamics. They should have slowly rising rotation curves (which is true), and they should deviate systematically from the Tully-Fisher (TF) relation.

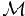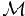The expected departure from the TF relation goes in the sense that LSB galaxies should rotate slowly for their luminosity. This follows simply because R_h is large for a given Mitalic _h, and V² = G Mitalic / R. There is some freedom to tune the amount of the shift, so long as it is systematic with surface brightness. It would not fit nicely into this picture if there were zero shift.

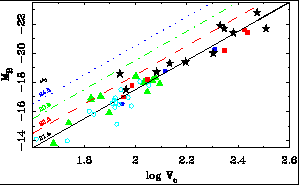
Figure 1. The luminosity-rotation velocity (Tully-Fisher) relation. Data are shown for galaxies with V_c measured from the flat part of resolved, extended rotation curves (solid symbols; de Blok et al. 1996) and for some with recent high quality velocity widths (open symbols; Matthews et al. 1998). Symbols distinguish different bins of central surface brightness - stars: µ₀ < 22; squares: 22 < µ₀ < 23; triangles: 23 < µ₀ < 24; filled circles: µ₀ > 24. Galaxies with open symbols predominantly have µ₀ > 23. The data do not distinguish themselves by surface brightness in this diagram. The lines are not fits to the data, but have the ``virial'' slope of -10. They are labeled by a corresponding central surface brightness illustrating the systematic shift that is expected from simple arguments (see text).

This is exactly what is observed (Figure 1). Regardless of surface brightness, LSB galaxies fall on the same ⁽¹⁾ TF relation with the same normalization as HSB galaxies. The shift I expected is illustrated by the lines in Figure 1, and clearly does not occur.

¹ This result has been independently obtained by Zwaan et al. (1995), Sprayberry et al. (1995), Hoffman et al. (1996), and Tully & Verheijen (1997). It has been disputed by Matthews et al. (1998), who suggest that some faint LSB galaxies fall systematically below the TF relation. This is a result of comparing to a TF relation with a shallow slope determined from a fit to bright galaxies. The data of Matthews et al. are consistent with other data (Fig. 1). Indeed, they add weight to the faint end which is much needed for constraining the slope.