


3.1 Theoretical Arguments for the Spin Paradigm
There is significant theoretical basis for this paradigm as well. Several models of relativistic jet formation (Blandford & Znajek 1977, Punsly & Coroniti 1990) indicate that the jet power should increase as the square of the black hole angular momentum
where Bp is the strength of the poloidal
(vertical/radial) magnetic
field threading the ergospheric and horizon region of the rotating hole.
In this model rotational energy is extracted via a Penrose-like process:
the frame-dragged accretion disk is coupled to plasma above and outside the
ergosphere via the poloidal magnetic field; some plasma is pinched and
accelerated upward while some disk material is diverted into negative
energy (retrograde) orbits inside the ergosphere, removing some of the
hole's rotational energy. The key parameter determining the efficiency
of this process is the strength of the poloidal magnetic field. The
standard approach
(e.g., Moderski &
Sikora 1996)
to estimating Bp
is to set it equal to B
for Class B (radio galaxy/ADAF) and Class A (quasar/standard disk) objects,
respectively. Note that, while the jet is not accretion-powered in this
model, the efficiency of extraction is still essentially linear in
Livio et al. (1999)
have pointed out that taking Bp
where (H/R) is the
ratio of disk half-thickness to radius in the jet acceleration region. For
thin disks this yields a jet power of only
Ljet = 4 x 1044 erg s-1
m91.1
(
Figure 1. Schematic representation of four
possible combinations of
Figure 1 summarizes the main features of the
accretion and
spin paradigms and shows the four possible combinations of high and low
accretion rate and black hole spin. It is proposed that these states
correspond to different radio loud and quiet quasars and galaxies. In the
figure poloidal magnetic field strengths are estimated from equation
(6), but (H/R) is of order unity for the low
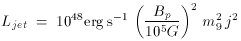
 , the dominant azimuthal magnetic field
component given by the disk structure equations, yielding
, the dominant azimuthal magnetic field
component given by the disk structure equations, yielding
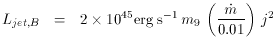
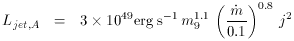
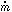 .
.
 B
B may greatly
overestimate the jet power from this process. Using dynamo arguments they
propose that a more realistic estimate for the equilibrium poloidal
magnetic field is
may greatly
overestimate the jet power from this process. Using dynamo arguments they
propose that a more realistic estimate for the equilibrium poloidal
magnetic field is
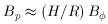
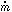 / 0.1)1.2
j2
- less than the observed radio power of the strongest sources and
much less than their inferred total jet power
(see Bicknell, these proceedings, and
Bicknell 1995).
However, there are several reasons for believing that even with equation
(6) the field still can be quite large in many cases, and the
jet power still comparable to equations (4) and (5).
Firstly, for advective disks (both the accretion-starved kind
[
/ 0.1)1.2
j2
- less than the observed radio power of the strongest sources and
much less than their inferred total jet power
(see Bicknell, these proceedings, and
Bicknell 1995).
However, there are several reasons for believing that even with equation
(6) the field still can be quite large in many cases, and the
jet power still comparable to equations (4) and (5).
Firstly, for advective disks (both the accretion-starved kind
[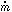 << 1]
and the super-Eddington kind [
<< 1]
and the super-Eddington kind [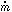
 1]) the disk is
geometrically thick (H/R ~ 1), yielding Bp
1]) the disk is
geometrically thick (H/R ~ 1), yielding Bp
 B
B even within the dynamo
argument. Thick disks also can occur for an even broader range of accretion
rate when the hole and disk spin axes are misaligned: because of the
Lens-Thirring effect, the gas follows inclined orbits that do not close,
creating shocks and dissipation that
bloats the disk into a quasi-spherical, inhomogeneous inflow
(Blandford 1994).
Furthermore, even when H << R, inside the last stable
orbit (or in any other region
of the disk where the infall velocity suddenly approaches the free-fall speed)
conservation of mass will cause a drop in density and pressure. The toroidal
field may then be dynamically important, buckling upward out of the plunging
accretion flow, resulting in Bp being comparable to
B
even within the dynamo
argument. Thick disks also can occur for an even broader range of accretion
rate when the hole and disk spin axes are misaligned: because of the
Lens-Thirring effect, the gas follows inclined orbits that do not close,
creating shocks and dissipation that
bloats the disk into a quasi-spherical, inhomogeneous inflow
(Blandford 1994).
Furthermore, even when H << R, inside the last stable
orbit (or in any other region
of the disk where the infall velocity suddenly approaches the free-fall speed)
conservation of mass will cause a drop in density and pressure. The toroidal
field may then be dynamically important, buckling upward out of the plunging
accretion flow, resulting in Bp being comparable to
B (Krolik 1999).
(Krolik 1999).
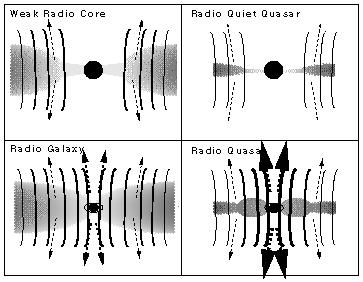
 and j, drawn roughly to scale.
The horizon interior to the hole is black, while the boundary of the
ergosphere (the ``static limit'') is
represented by an ellipse 0.5 x 1.0 Schwarzschild radius in size.
Top panels depict non-rotating, Schwarzschild holes (j -> 0),
bottom panels Kerr holes (j -> 1).
Left panels show low accretion rate (ADAF) tori, right panels high accretion
rate standard disk models.
However, in the lower right panel the region of the disk
experiencing significant frame dragging is bloated (c.f.
Blandford 1994).
Widths of poloidal magnetic field lines and jet arrows are proportional
to the logarithm of their strength.
and j, drawn roughly to scale.
The horizon interior to the hole is black, while the boundary of the
ergosphere (the ``static limit'') is
represented by an ellipse 0.5 x 1.0 Schwarzschild radius in size.
Top panels depict non-rotating, Schwarzschild holes (j -> 0),
bottom panels Kerr holes (j -> 1).
Left panels show low accretion rate (ADAF) tori, right panels high accretion
rate standard disk models.
However, in the lower right panel the region of the disk
experiencing significant frame dragging is bloated (c.f.
Blandford 1994).
Widths of poloidal magnetic field lines and jet arrows are proportional
to the logarithm of their strength.
 cases,
and also for the high
cases,
and also for the high  Kerr case
due to Lens-Thirring bloating of
the inner disk. Otherwise (H/R) is calculated from the electron
scattering/gas pressure disk model of
Shakura & Sunyaev
(1973),
and disk field strengths are computed from that paper or from
Narayan et al. (1998),
as
appropriate. The logarithms of the resulting poloidal field strengths, and
corresponding jet powers, are represented as field line and jet arrow widths.
In the Kerr cases, the inner disk magnetic field is significantly enhanced
over the Schwarzschild cases, due in part to the smaller last stable orbit
(flux conservation) and in part to the large (H/R) of the bloated
disks.
The high accretion rate, Schwarzschild case has the smallest field -
and the weakest jet - because the disk is thin, the last stable orbit is
relatively large, and the Keplerian rotation rate of the field there is much
smaller than it would be in a Kerr hole ergosphere.
Enhancement of the poloidal field due to the buoyancy process suggested by
Krolik (1999)
is ignored here because we find it not to be a factor
in the simulations discussed below. If it were important,
then the grand scheme proposed here would have to be re-evaluated, as the
effect could produce strong jets (up to the accretion luminosity in power)
even in the plunging region of Schwarzschild holes. Then even the latter
would be expected to be radio loud as well
(Ljet ~ 1043-46 erg s-1).
Kerr case
due to Lens-Thirring bloating of
the inner disk. Otherwise (H/R) is calculated from the electron
scattering/gas pressure disk model of
Shakura & Sunyaev
(1973),
and disk field strengths are computed from that paper or from
Narayan et al. (1998),
as
appropriate. The logarithms of the resulting poloidal field strengths, and
corresponding jet powers, are represented as field line and jet arrow widths.
In the Kerr cases, the inner disk magnetic field is significantly enhanced
over the Schwarzschild cases, due in part to the smaller last stable orbit
(flux conservation) and in part to the large (H/R) of the bloated
disks.
The high accretion rate, Schwarzschild case has the smallest field -
and the weakest jet - because the disk is thin, the last stable orbit is
relatively large, and the Keplerian rotation rate of the field there is much
smaller than it would be in a Kerr hole ergosphere.
Enhancement of the poloidal field due to the buoyancy process suggested by
Krolik (1999)
is ignored here because we find it not to be a factor
in the simulations discussed below. If it were important,
then the grand scheme proposed here would have to be re-evaluated, as the
effect could produce strong jets (up to the accretion luminosity in power)
even in the plunging region of Schwarzschild holes. Then even the latter
would be expected to be radio loud as well
(Ljet ~ 1043-46 erg s-1).