


The standard gravitational lens theory is valid for weak stationary
gravitational fields. For small angle deviations, and
when the typical size of the deflector is much
smaller than the propagation medium, it is possible to use the
thin lens approximation
(Blandford &
Kochanek 1988).
The lens is achromatic and acts
as a plane of matter with a projected surface mass
density  (
(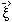 ).
).
The angular position of the source  is related to the angular position of the image
is related to the angular position of the image  through the lensing equation which expresses the simple geometrical
relationship shown in Fig. 3:
through the lensing equation which expresses the simple geometrical
relationship shown in Fig. 3:
with :
Dds = angular diameter distance from deflector
to source; Ds = angular diameter distance from observer
to source.
For a ray crossing the lens with impact parameter
where
with :
A ray is deflected with the concavity of the trajectory
oriented toward the local gravity field vector. The
gradient of the potential plays a similar role as a gradient
of index (1 - 2
But natural gravitational lenses like cluster of galaxies are highly
non-linear: the deflection parameter is not proportional
to the impact parameter, and the lens does not have
any focal length. The lens eventually
focuses onto large caustic sheets. Therefore, a cluster may
only focus a few bundles of rays from a source onto
an observer (the gravitational lens is then incorrectly
said to be ``focusing''). This corresponds to the so-called
strong lensing regime of the lens which produces multiple
images when the local mass density
Using the magnification axes for the angular
coordinates equation (1) can be written as :
where
and
The flux magnification µ is given by the
determinant of the magnification tensor d
If the shear parameter
with D = DdDds / Ds.
If the shear
Except for some unusual lenses, a general mass
distribution
For gravitational images
Etherington (1933)
demonstrated that the local surface brightness of an
image point is equal to the surface brightness of the antecedent point
on the source viewed without the
deflector. For an observer this has the deceiving
consequence that the apparent surface brightness of
objects is conserved : the contrast on the sky of faint
distant galaxies will not be changed by the lens (cf
sect. 3).
But this theorem provides one of the best
constraints for lens modeling
(Kochanek et
al. 1989,
see sect. 3.4). However, an amplification of light is obtained from
the geometrical magnification of the images. This is
particularly interesting for spectroscopy of magnified
sources. Note that for a point-like object like a QSO,
the total amplification of light and the image position will be the
only observable parameters.
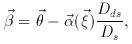
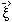 , the
deviation angle depends on the projected mass distribution
, the
deviation angle depends on the projected mass distribution  (
(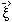 ). More precisely, the
deflection angle depends on the
gradient of the 2D-potential in the deflector plane,
). More precisely, the
deflection angle depends on the
gradient of the 2D-potential in the deflector plane,
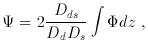
 is the three dimensional
potential, which
can be derived from
is the three dimensional
potential, which
can be derived from  (
(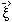 ) through the
Poisson equation (3):
) through the
Poisson equation (3):
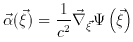
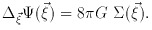
 / c2)
in classical optics
(Schneider, Ehlers
& Falco 1992).
/ c2)
in classical optics
(Schneider, Ehlers
& Falco 1992).
 (
(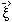 )
is large enough.
Figure 4 schematically illustrates a strong
lensing configuration with 3 rays crossing at the observer's position.
)
is large enough.
Figure 4 schematically illustrates a strong
lensing configuration with 3 rays crossing at the observer's position.
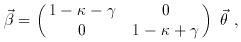
 and
and  are respectively the convergence (Ricci
focusing) due to the matter within the ray, and
shear (Weyl focusing) due to the mass outside the beam,
of the (quadrupole) lens
(Schneider, Ehlers
& Falco 1992):
are respectively the convergence (Ricci
focusing) due to the matter within the ray, and
shear (Weyl focusing) due to the mass outside the beam,
of the (quadrupole) lens
(Schneider, Ehlers
& Falco 1992):
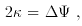
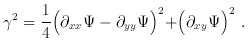
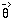 / d
/ d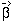 :
:
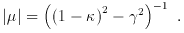
 is
zero, we have the equivalent of a uniform sheet of matter. Due to the
local mass density, a small beam of light crossing the
lens will have just an homothetic shrinking of its cross
section by a factor ( 1 -
is
zero, we have the equivalent of a uniform sheet of matter. Due to the
local mass density, a small beam of light crossing the
lens will have just an homothetic shrinking of its cross
section by a factor ( 1 -  )2.
It can be see from expression (4) that an uniform sheet of
matter focuses all the rays coming from a source onto
the observer if
)2.
It can be see from expression (4) that an uniform sheet of
matter focuses all the rays coming from a source onto
the observer if  = 1. This
condition can be explicitly written as
(Blandford &
Kochaneck 1988;
Schneider, Ehlers &
Falco 1992):
= 1. This
condition can be explicitly written as
(Blandford &
Kochaneck 1988;
Schneider, Ehlers &
Falco 1992):
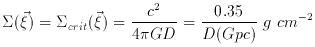
 is non-zero the
cross section will have an extra ellipticity induced by the differential
deflection of the rays along the local gravity vector
resulting from the total mass of the lens. This explains
the formation of arclets and the weak statistical
distortion of background galaxies observed at the
periphery of clusters (Figs. 4 and
5).
is non-zero the
cross section will have an extra ellipticity induced by the differential
deflection of the rays along the local gravity vector
resulting from the total mass of the lens. This explains
the formation of arclets and the weak statistical
distortion of background galaxies observed at the
periphery of clusters (Figs. 4 and
5).


Figure 5. Distortion field generated by a lens. The top panel shows
the grid of randomly distributed
background sources as it would be seen in the absence of the
lens. The projected number density corresponds to the Tyson population
at a limiting magnitude B = 28
(Tyson 1988).
The bottom panel shows the
same population once they are distorted by a foreground
(invisible) circular cluster
with a typical velocity dispersion of 1300 km s-1.
The geometrical signature of
the cluster is clearly visible. The potential can be
recovered by using the formalism defined in
part 4. In this
simulation, the sources are at z = 1.3, and the cluster at
z = 0.15.
 (
(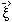 ) focuses multiple
images onto the observer if its surface density exceeds
) focuses multiple
images onto the observer if its surface density exceeds  crit at
some point
crit at
some point 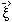 (see part 3 on marginal lenses).
From expression (1) it can be seen that the deviation angle is
proportional to a geometrical term that only depends on the angular distances
of the deflector and sources. If the redshifts of the source and
the lens are known, the
astrometric positions of the images will depend on the geometry of the
universe. This could be used as a tool for cosmography (cf
part 5).
(see part 3 on marginal lenses).
From expression (1) it can be seen that the deviation angle is
proportional to a geometrical term that only depends on the angular distances
of the deflector and sources. If the redshifts of the source and
the lens are known, the
astrometric positions of the images will depend on the geometry of the
universe. This could be used as a tool for cosmography (cf
part 5).