2.4 The Non Singular Squeezed Isothermal Potential
For cluster of galaxies, the simplest 2-dimensional potential currently used to model multiple images was introduced by Kovner (1987a, b) and Blandford & Kochanek (1987). It is a non-singular squeezed isothermal sphere of the form:
where
The one dimensional velocity dispersion
An elliptical lens is astigmatic. It produces 2
caustics : one internal caustic with a diamond shape
responsible for the largest arcs, and a pseudo-elliptical
external caustic that is responsible for a possible radial
image (Fig. 8). This external caustic exists
only if the potential has a core radius, that is to say if the surface mass
density is approximately flat with no singularity for
When the arcs are broken into several images it is
sometimes possible to observe in exceptional seeing the
inversion of images (parity change) predicted by the modeling. This is a
clear signature of a gravitational lens effect and it has been
observed in the clusters Cl2244-02
(Fig. 6) and Cl0024+1654
(Kassiola, Kovner &
Fort 1992).
Most of the luminous arc configurations actually
observed can be reproduced fairly well with this mathematically simple
elliptical potential. Some typical examples of the possible
geometry of arc systems are given in the panels of
Fig. 8. However,
the model is acceptable only for small ellipticity. When the
axis ratio b/a is larger than 0.5, the isodensity contours
of the potential tend toward a funny peanut
shape which has no physical meaning.
Kassiola & Kovner
(1993a)
have now proposed a new analytic expression for the
potential with elliptical mass distributions
that are realistic at large ellipticities. They can eventually be adjusted to
any distribution of light in the cluster center (smoothed galaxy light
distribution, X-rays, faint visible halos of giant central galaxies, etc...).
Last but not least, possible naked cusp configurations like
hyperbolic-umbilic catastrophes can form ``uglier'' images with
very strong amplification
(Miralda-Escudé 1993a).
Such images result from the merging of 5 images, but have not
been observed to date, despite a reasonable probability of occurrence.
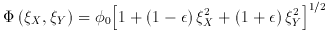
X and
Y
are scaled to the core radius c ,
= (a2 -
b2) / (a2 + b2), and
0 = 4 
(
1D / c)2 c
Dds / Ds.
1D can be
related to the observed line of sight velocity dispersion
of cluster galaxies obs. For
a circular potential this relation is simple:
21D = 4 / 3 2obs
(Mellier et
al. 1993).
Figure 7. Formation of an Einstein ring and two
opposite arcs by a
singular isothermal sphere. The left panel shows the position of the
source in the source plane with respect to the optical axis. The central
and the right panels show the images for the case of perfect alignment and
for a small offset between the source and the lens position.
= 0
(
( = 1) = ( = 0).)
Figure 8. Behavior of the gravitational distortion induced
by an elliptical potential as a function of source
position. The top left panel shows the shape of the source in the source
plane. The second panel shows 10 positions of the source in the source
plane (referenced from 1 to 10) with respect to a simulated cluster
lens. The full drawn lines are the inner and outer caustics. Panels 3
to 12 show the inner and outer critical lines and the shape of the
image(s) of the lensed source. Note positions 6 and 7 which correspond
to cusp catastrophes, and position 9 which is a typical fold
catastrophe. On the fifth panel we see two inner merging images forming
a typical radial arc (from
Kneib 1993,
PhD thesis).