The idea that supermassive black holes are generic components of galactic nuclei has come to be widely accepted, due largely to the secure detection of 10⁶-10^9.5 M dark objects at the centers of about a dozen galaxies. ¹ The mean mass of these objects - of order 10^-2.5 times the mass of their host galaxies - is consistent with the mass in black holes needed to produce the observed energy density in quasar light given reasonable assumptions about the efficiency of quasar energy production. ^{2, 3} The black hole paradigm also explains in a natural way many of the observed properties of energy generation in active galactic nuclei (AGNs), ⁴ and a model in which elliptical galaxies form from the mergers of disk galaxies whose bulges contain black holes has been shown to be consistent with the so-called ``core fundamental plane,'' the relation between the central parameters of early-type galaxies. ⁵ However it has long been clear that the dynamical influence of a supermassive black hole can extend far beyond the nucleus if a substantial number of stars are on orbits that carry them into center. ^{6, 7} Recent work, discussed here, has expanded on this idea and given support to the view that nuclear black holes may be important for understanding many of the systematic, large-scale properties of galaxies, including the absence of bars in most disk galaxies, the shapes of spiral galaxy rotation curves, and the fact that elliptical galaxies come in two, morphologically-distinct families. To the extent that the growth of black holes is dependent on the global morphology of their host galaxies, this link between black holes and galaxy structure may imply a feedback mechanism that determines what fraction of a galaxy's mass ends up in the central singularity.

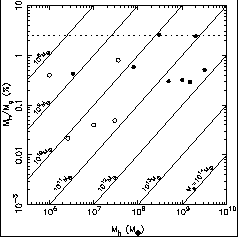
Figure 1. Black hole masses Mh, in units of the solar mass, and mass fractions Mh / Mg, with Mg the mass of the bulge, for 13 galaxies with securely-detected black holes. 9 Filled circles are early-type galaxies (S0, E, Sa); open circles are late-type galaxies (Sb, Sc). The dashed line is the critical mass ratio that enforces axisymmetry in a triaxial bulge. 35

Dressler & Richstone ⁸ pointed out a decade ago that the ratio of the masses of the dark objects in M31 and M32 was 5-10, ``closer to the ratio of spheroid luminosities (~ 15) than it is to the ratio of total luminosities (~ 70).'' Since then, the approximate proportionality between black hole mass and bulge mass has held up fairly well. Figure 1, based on Richstone's ⁹ recent compilation, shows black hole masses M_h vs. mass ratios M_h / M_g for 13 galaxies; M_g is defined as the total luminous mass in the case of elliptical galaxies and as the bulge mass in the case of disk galaxies. (Two galaxies with questionable black hole detections, NGC 3379 and NGC 4486b, were omitted.) Figure 1 suggests a typical value for M_h / M_g of ~ 0.5% and an upper limit of ~ 3%. There is a trend of increasing M_h / M_g with M_h which probably just reflects the shortage of very bright and very faint galaxies in the sample. Perhaps more significant is the tendency of M_h / M_g to depend on Hubble type: the largest mass fractions are seen in early-type galaxies, S0's and E's, and the smallest in late-type galaxies, Sb's and Sc's. This trend is reproduced even within the (essentially complete) sample of galaxies from the Local Group: M_h / M_g for the Milky Way and M31 are 0.02% and 0.05% while the elliptical galaxy M32 has M_h / M_g 0.4%. (M33 has neither a detectable black hole nor a detectable bulge ¹⁰).

Uncertainties in the determination of M_h are often large ¹ but bulge masses can be very uncertain too. One source of systematic error that might introduce a spurious dependence of M_h / M_g on Hubble type has been pointed out by Kormendy. ¹¹ Bulges are difficult to disentangle photometrically from disks and the decomposition is most difficult in late-type spirals which have the smallest bulge-to-disk ratios. A blind decomposition assuming an exponential disk tends to give spuriously large bulge luminosities, hence overly small values of M_h / M_g, since many disks have steeper-than-exponential profiles near the center. The luminosity and mass of the Milky Way bulge, which has the lowest value of M_h / M_g in Figure 1, are especially poorly known. The bulge mass used in Figure 1 was taken from Kent's ¹² model which was based on K-band photometry with (large) corrections for absorption and for the light from the disk. While Kent's model accounts nicely for the kinematics of a wide range of bulge tracers, some components of the bulge are observed to fall off more steeply ^{13, 14} suggesting a possibly smaller total mass and a larger M_h / M_g.

Nevertheless it is reasonable to expect lower values of M_h / M_g in galaxies with small bulge-to-disk ratios since these galaxies are the least likely to have experienced the strong non-axisymmetric distortions that are believed necessary for driving large amounts of gas into the nucleus and feeding the black hole. ¹⁵ For instance, if tidal encounters or mergers during the quasar epoch were responsible for black hole growth, ¹⁶ the smallest mass accumulations would be expected in late-type spirals which have presumably suffered the fewest such interactions. Other factors that might limit the accumulation of mass in the nuclei of late-type galaxies are their generally weaker bars ¹⁷ and the fact that gas flows in barred galaxies with small bulges tend not to form shocks. ¹⁸

The argument that large-scale nonaxisymmetries in the stellar distribution are necessary for the formation of black holes is based on the stringent requirements that quasar luminosities place on fueling mechanisms. ¹⁵ Gravitational torques from a stellar bar - induced by galaxy interactions or internal self-gravitational instabilities, or both - can remove much of the angular momentum from the interstellar medium on kiloparsec scales, allowing a large fraction of a galaxy's gas to approach the nucleus in a dynamical time. This picture derives some support from the observation that the host galaxies of AGNs often have close companions or substantial asymmetries. ^{19, 20} However the evidence for a direct link between stellar bars and nuclear activity is weak at best. Neither the detection rate nor the emission-line strength of AGNs appear to be influenced by the presence of a stellar bar, ^{21, 22} and the majority of barred galaxies exhibit no significant nuclear activity.

The relevance of such data to theories of black hole formation is difficult to judge because the bars that we see now need not be the ones that were responsible for creating the black holes. Indeed, the accumulation of mass at the center of a barred galaxy can weaken or even dissolve the bar by changing the major families of orbits. ^{23, 24} N-body simulations ^{25, 26} suggest that bar disruption follows rapidly after several percent of a disk's mass has accumulated in a compact central object. This mechanism may help to account for the scarcity of luminous AGNs in the current universe ²⁷ but it does not shed light on why barred and unbarred galaxies show roughly the same level of activity.

Sellwood & Moore ²⁸ have recently proposed a model that reconciles the bar-driven formation of black holes at early times with the apparent inability of bars to generate nuclear activity at the current epoch. They simulated the evolution of a stellar disk in which a central mass was grown at a rate that depended on the strength of the bar. They found, in agreement with earlier studies, that the bar was substantially weakened once a few percent of the disk mass accumulated at the center. As the central object grew, it pulled in matter from the disk, forming a bulge with much greater total mass. Sellwood & Moore then simulated infall of matter from the halo onto the disk by adding additional particles on circular orbits at large radii. Even after the mass of the disk had grown by a factor of ~ 4, no bar formed because the inner Lindblad resonance resulting from the newly-formed bulge suppressed the bar-making instability. ²⁹ The galaxy that resulted from this experiment resembled a late-type, unbarred spiral with a realistically flat inner rotation curve. Sellwood & Moore suggest that bars may nevertheless still form in real galaxies due to large perturbations or tidal encounters that can overwhelm the damping effect of the resonance. Such bars would be prohibited by the ILR from channeling gas into the nucleus, however, thus limiting their activity in the current universe.

Large-scale stellar bars like those in Sellwood & Moore's simulations can reduce the angular momentum of the gas by only an order of magnitude or so. ³⁰ How the gas is funneled into the inner few parsecs is unclear but such transport probably requires non-axisymmetric distortions of the stars and gas on still smaller scales. ^{31, 32, 33} Any mechanism that enforced axisymmetry in the dominant mass component of the bulge would therefore be expected to limit the mass of a central object regardless of the presence of a large-scale bar. One such mechanism has long been known. The box orbits that support a triaxial stellar system are strongly influenced by a central point mass, since stars on box orbits pass arbitrarily close to the center after a long enough time. ^{6, 7} A triaxial bulge containing a central black hole would be expected to evolve toward rounder or more axisymmetric shapes as the box orbits gradually lost their distinguishability, in much the same way that bars are weakened or destroyed by central mass concentrations.

An early study ³⁴ of the effect of a central point mass on a triaxial galaxy found only a modest degree of evolution, but the softening length used was comparable to the radius of influence of the black hole and so the degree of orbital evolution was probably strongly underestimated. Much more dramatic evolution was seen in a recent study ³⁵ based on a hybrid N-body code with individual particle timesteps. The authors found rapid evolution to nearly complete axisymmetry once the central mass exceeded ~ 2.5% the mass of the galaxy. This mass ratio is interestingly close to the largest values observed in real galaxies (Figure 1): the current record-holders, NGC 3115 and NGC 4342, both have M_h / M_g 0.025. The agreement suggests that M_h / M_g may be limited by a feedback mechanism that turns off the supply of fuel when the black hole grows large enough to force its bulge into an axisymmetric shape. Stated differently, black holes may sometimes grow as large as the morphology of their host spheroids permit.

It is clear from Figure 1 that not all bulges contain black holes with M_h 0.025M_g, but it is not difficult to think of additional mechanisms that would limit or reduce M_h / M_g. The efficiency with which stellar bars drive gas into the bulge could differ from galaxy to galaxy, as discussed above. The central parts of some galaxies might reach an axisymmetric state through processes unrelated to the presence of a black hole. ³⁶ On smaller scales, the back-reaction of the energy emitted from the black hole on the accretion flow might limit black hole masses. ^{37, 38} Successive mergers between galaxies already containing supermassive black holes could result in a gravitational slingshot if a third black hole is brought into a nucleus that contains an uncoalesced binary. ³⁹ Mergers after the quasar epoch would also tend to reduce the average value of M_h / M_g by converting disks to spheroids. Typical disk-to-bulge ratios for S0 galaxies like NGC 3115 and NGC 4342 are of order unity; a merger between two such galaxies would reduce M_h / M_g by a factor of ~ 2 (assuming no further growth of the black holes), perhaps accounting for some of the vertical scatter in Figure 1.

Dissipationless mergers between disk galaxies tend to create strongly triaxial objects. ⁴⁰ Adding a dissipative component greatly reduces the triaxiality, ^{41, 42} presumably via destabilization of the box orbits as gas deepens the potential. Similar behavior would be expected following the merger of two galaxies containing black holes: the merger-induced triaxiality would gradually be destroyed by the central black hole at a rate determined by M_h / M_g in the merged system. Merritt & Quinlan ³⁵ find that a black hole with M_h / M_g = 0.3%, close to the average value for the elliptical galaxies in Figure 1, destroys triaxiality in roughly 100 periods of the half-mass orbit. This works out to ~ 5 x 10⁹ years for a typical early-type galaxy with M_B = -19 using observed scaling relations. ^{43, 44, 45} Fainter galaxies are denser, i.e. have shorter crossing times. It follows that most elliptical galaxies fainter than M_B -19 should have evolved to axisymmetric shapes by now (even if they were not axisymmetric initially), while brighter ellipticals could still be triaxial. In fact the Hubble-type distribution of elliptical galaxies undergoes a systematic change at about this luminosity and bright ellipticals appear to be moderately triaxial as a class. ⁴⁶ The sudden increase of elliptical galaxy radio luminosity at M_B -19 has also been attributed to a greater degree of triaxiality among bright ellipticals. ^{47, 48}

Bright and faint ellipticals differ also in the steepness of their central luminosity profiles: faint ellipticals have ~ r^-2 near the center while bright ellipticals have shallower cusps, ~ r^-1 - r⁰. ^{49, 50, 51} Density cusps would themselves induce chaos in the box orbits of a triaxial galaxy, ^{52, 53} and the steep cusps in faint ellipticals would cause these galaxies to evolve to nearly axisymmetric shapes after a sufficiently long time even in the absence of nuclear black holes. ⁵⁴ But the orbital evolution induced by even the steepest cusps is no more rapid than that caused by a black hole with M_h / M_g 0.005, ⁵⁵ the average value for the elliptical galaxies in Figure 1. It follows that black holes are probably more important than central density cusps for producing orbital evolution in the majority of elliptical galaxies. To the extent that M_h / M_g is independent of M_g, dynamical evolution timescales in triaxial galaxies should therefore scale roughly with their crossing times, as assumed above.

Kormendy and Bender ⁵⁶ have noted that many dynamical properties of elliptical galaxies correlate with their isophotal shapes, either disky or boxy. Boxy Es rotate more slowly than disky Es and are more likely to exhibit the dynamical signatures of triaxiality. An interesting question, not addressed by Kormendy and Bender, is why triaxiality should correlate with boxiness. It is tempting to associate ``boxy isophotes'' with ``box orbits'' and hence with triaxiality but the tube orbits that make up axisymmetric galaxies are equally good at generating boxy isophotes. ⁵⁷ Boxiness results from a non-smooth population of phase space, i.e. from a distribution function that is peaked around orbits with a narrow range of shapes, ⁵⁸ whether tubes or boxes. Eliminating boxiness requires a ``smoothing out'' of phase space and the orbital evolution induced by a central black hole has just this effect. N-body simulations provide some support for this idea: boxy, triaxial systems evolve - following an increase in their central densities - into axisymmetric ones with accurately elliptical isophotes. ³⁵ Boxy isophotes may therefore be an indication that the central black hole has not had sufficient time (reckoned since the most recent merger, say) to strongly influence the orbital distribution, hence to destroy the triaxiality. Boxy galaxies constructed primarily from tube orbits would not be affected by a central mass, which may explain the persistence of strong boxiness at the centers of many disk galaxies ⁵⁹ and in some faint, rapidly-rotating ellipticals. ⁶⁰

The smoothing effect that a black hole has on the orbital population of a triaxial galaxy is an example of ``chaotic mixing,'' the tendency of the phase space density in a chaotic system to approach a constant value at all points on the energy surface. ^{61, 62} Chaotic mixing is responsible for the fact that complex dynamical systems like gases exhibit a much narrower range of properties than they would if their constituent particles were free to populate phase space in arbitrary ways. ⁶³ In the same manner, the observed regularity in elliptical galaxy properties may be attributable in part to chaotic mixing induced by nuclear black holes. One example, just discussed, is the tendency of black holes to convert boxy, triaxial galaxies into axisymmetric ones with elliptical isophotes - i.e. to restrict the allowed range of shapes. On a deeper level, the distribution function of an axisymmetric galaxy formed in this way would be biased toward forms for f that are as nearly constant as possible. The most general f for an axisymmetric galaxy has the form f (E, L_z, I₃) with I₃ the third integral. There are generally many three-integral f's that are consistent with a given axisymmetric density law (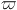, z); ⁶⁴ among these, the smoothest f is the one that is constant with respect to the third integral, f = f (E, L_z). This argument suggests that the phase space density of stars in an axisymmetric galaxy that had evolved, via black-hole-induced chaos, from a more general triaxial shape should depend only weakly on the third integral. It is interesting that detailed modelling of M32, a galaxy that is old compared to expected timescales for chaotic mixing, ⁶² yields a best-fit f f (E, L_z). ⁶⁵ The extreme non-uniqueness of galactic models, ⁶⁶ for so long the bane of stellar dynamicists, may largely disappear once the constraints imposed by black-hole-induced evolution are more fully understood.

This work was supported by NSF grants AST 93-18617 and AST 96-17088 and by NASA grant NAG 5-2803. I thank E. Athanassoula, J. Barnes, F. Combes, D. Friedli, C. Joseph, S. McGaugh, A. Quillen, J. Sellwood and M. Valluri for useful discussions and for comments on the manuscript.