


A.1. Extent of the Ionized Region
The size of the H II region has been calculated by considering photoionization and recombination of hydrogen, along with the absorption due to the dust grains. The presence of the dust component reduces the size of the ionized region, (RHII), compared to that of pure gas Stromgren sphere considerably, depending on the density and the gas to dust ratio. The dust grains can exist in principle, only beyond a radial distance, say rsubl, depending on its sublimation temperature and the local radiation field. In practice, the actual distance beyond which the dust exists, say rfit, is determined by the model fitting of the observed SED, by radiative transport calculations through the dust. The rfit is often much larger than rsubl.
Hence, whether one encounters a dusty Stromgren sphere or not, is determined by the type of the star / integrated spectrum of the cluster; radial density distribution around the central star; and rfit. We call it a Case A, if the ionized region extends into the region where the gas the and dust co-exist. The other case of entire ionized region devoid of any dust grains is termed Case B. So for Case B, the extent of the H II region can be obtained by solving the equation,
where, N(r) is the Lyman continuum photon flux,
For m = 0, 1, 2 equation(A1) can be solved easily by using the
boundary condition
where, NLyc is the total number of Lyman continuum
photons emitted per second by the embedded exciting star / star cluster
and r* is an effective stellar radius (with volume
equal to the
sum of that of all the stars of the embedded cluster; as it turns out,
results are extremely insensitive to r*).
In case A however, the ionizing (Lyman continuum) photons experience further
attenuation due to direct absorption by the dust,
so the modified radiation transfer equation would be,
where 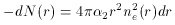
 2 is
the recombination coefficient for hydrogen (for recombinations to all states
except the ground state) and ne is the number
density of electrons or H+ ions (for a pure H II region),
which in our case is the gas number density (ng) and
may be given by,
2 is
the recombination coefficient for hydrogen (for recombinations to all states
except the ground state) and ne is the number
density of electrons or H+ ions (for a pure H II region),
which in our case is the gas number density (ng) and
may be given by,
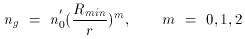

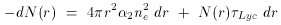
 Lyc refers
to the optical depth of dust at
Lyc refers
to the optical depth of dust at
 < 912 Å.
We solve the above equation, using the boundary conditions,
< 912 Å.
We solve the above equation, using the boundary conditions,