The notion that a galaxy cluster forms via gravitational instability within an expanding universe was first discussed by van Albada (1961). The first numerical studies of cluster stability with 10-100 particles were carried out by von Hoerner (1960) and Aarseth (1963). An investigation of the virialisation process using several hundred particles was carried out by Henon (1964) and Peebles (1970). The assumption being that the ``galaxies'' had already collapsed prior to the turn around of the cluster. From these first simulations it was clear that one could form an equilibrium cluster of particles with global properties not too unlike the theorists ``ideal'' Coma cluster.
White (1976) followed the evolution of 700 unequal mass particles expanding with the Hubble flow. In this case it was possible to follow the collapse of groups of particles prior to the formation of the cluster. However, these clumps of bound particles were erased during the collapse and virialisation of the final system. This work may have been the key motivation behind the seminal paper ``Core condensation within heavy halos...'' (White & Rees 1978). This paper argued that cooling and settling of baryons at the centres of dark matter halos was essential to the formation and survival of galaxies in dense environments. Although a valid description of galaxy formation, it is now apparent that this process is not necessary in order to resolve substructure within hierarchical models.
|
Figure 1. The hierarchical evolution of a galaxy cluster in a universe dominated by cold dark matter. Small fluctuations in the mass distribution are present but barely visible at early epochs. These grow by gravitational instability, merging and accretion of mass, eventually collapsing into virialised quasi-spherical dark matter halos. This plot shows a time sequence of 6 frames of a region of the universe that evolves into a cluster of galaxies. The colours represent the local density of dark matter plotted using a logarithmic colour scale. Linear over-densities are darker blue, whereas the non-linear collapsed regions attain over-densities of a million times the mean background density and are plotted as yellow/white. Each box is 10 Mpc on a side and the final cluster virial radius is 2 Mpc. |
In the 1980's more detailed cosmological models were developed in which the mass of the universe was dominated by collisionless particles. The linear power spectrum of density fluctuations was determined by the growth of fluctuations in the expanding universe and the temperature of the dark matter particle. The cold dark matter (CDM) model was born (Peebles 1983).
N-body simulations of cluster formation were used to constrain the hot dark matter model (White etal 1984) and most subsequent work has focussed on the cold dark matter model (CDM), the currently favoured scenario for structure formation in the universe. Warm dark matter has not received a great deal of attention in the literature - primarily because this model could not naturally produce a closure density of dark matter. Attention has now shifted from standard CDM models, which fail for a variety of reasons, to a Lambda dominated CDM universe. Since the universe is clearly not as simple as one might wish, alternative models such as warm or self interacting dark matter may become more popular. Perhaps the widespread acceptance of a positive Lambda term stems mainly from the fact that the most hierarchical model fails without its inclusion. Although a hierarchical universe can explain many fundamental observations, from the microwave background to clustering at high redshifts, we still know next to nothing about the physical nature of the dark matter.
Many of the numerical simulations during the 1980's focussed on a comparison between models and observations of large scale structure. Studies of individual halo properties were taken from large cosmological volume simulations. For example, Frenk etal (1985) and Quinn etal (1986) analysed the structure of dark matter halos that contained just a few thousand particles per object. Code development, ``volume renormalisation'' and faster computers lead to the ability to simulate individual clusters with more than 105 particles and with a force resolution of approximately 1-2% of the virial radius (Dubinski & Carlberg 1991, Warren etal 1992, Summers etal 1995, Tormen etal 1997, 1997, 1998). These simulations still produced smooth dark matter halos with very little surviving dark matter subhalos - although interesting results were found concerning the inner structure of halos and the formation and accretion history of halos.
Warren etal and Carlberg were the first to resolve the inner 10% of a halos
virial radius and claimed a power law slope
(r)
r-1. Later
simulations by
Navarro etal (1997)
revealed the remarkable scaling properties
of CDM halos across a wide range of mass scales, from dwarf galaxies to galaxy
clusters. Determining the central cuspy profile of dark matter halos is an
important but difficult computational problem and we have seen recent progress
in this area from many groups.
Analytic work concerning the overmerging problem began with White & Rees (1978) who discussed the various numerical and physical processes that could lead to the loss of substructure. Carlberg (1994) argued that particle-halo heating was the cause of overmerging, a result also claimed by van Kampen (1995). However the timescale for this process was at least a Hubble time whereas overmerging appeared on an orbital timescale. Moore etal (1996) argued that the resolution at that time was sufficient to overcome relaxation and tidally accelerated disruption by the finite mass background particles.
The physical processes of tidal disruption via halo-halo collisions and by the
global cluster potential take place on a more rapid timescale and could
explain the loss of substructure in the simulations prior to 1998
(Moore etal 1996
- the investigation of the importance of this process lead to the notion
of galaxy transformation in clusters by tidal heating - galaxy harassment.)
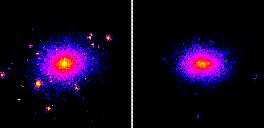
Tidal disruption is rapidly enhanced if halos are poorly resolved in
their central
regions (cf. Figure 2). The survival of dark
matter substructure depends
critically on the central density structure which in turn depends on the force
and mass resolution in a simulation. For example, if halos have resolved
singular density profiles
(r)
r-2, then
it is physically impossible to
entirely disrupt a satellite halo. Only through physical merging can such
halos be lost.
The key motivation behind the Seattle HPCC group (http://www-hpcc.astro.washington.edu/) was to construct a high performance parallel treecode (PKDGRAV) that could simulate the formation of cosmic structures with high resolution. The aim was to resolve sub-galactic halos with thousands of particles and ~ kpc force resolution. After a long testing program a set of accuracy parameters were chosen that allowed the correct growth of fluctuations to be followed on large scales, as well as accurately following the orbits of particles in the most dense regions.
|
Figure 2. The same cluster simulated in Figure 1 but with two different values of the softening length and keeping the particle mass fixed. The left panel shows a close up view of the inner 500 kpc of the last frame of Figure 1. In this case the softening was 0.2% of the virial radius. The right panel shows the same region of the same cluster but simulated with a softening length of 1.5% of the virial radius. The lack of substructure halos in the right panel demonstrates that softened halos are easily disrupted by tidal forces. |
The first simulation to finish was the 1.3 million particle ``Virgo'' cluster simulation presented in Moore etal (1998) and analysed by Ghigna etal (1998). This was a simulation of the formation of a single galaxy cluster within a standard CDM universe (Figure 1). The box size was 100 Mpc but a series of nested shells of different mass particles allowed the cluster to be resolved at high resolution. Many hundreds of dark matter subhalos could be found orbiting within the cluster - the overmerging problem was resolved. A higher resolution study of the same cluster demonstrates that the central density profile appears to have converged as have the global properties of the subhalos within the cluster (Ghigna etal 2000). (Similar high resolution studies were being carried out at the same time by several other groups (c.f. Klypin etal 1999, Colin 1999, Okamoto & Habe 1999, Jing 2000, Fukushige & Makino 2000).
It is interesting to see how numerical calculations are scaling with respect to algorithmic and computational developments. The cluster simulation by Peebles (1970) contained 300 particles and had a force resolution of order 100 kpc. The highest resolution simulation published to date is by Ghigna etal (2000) in which a cluster halo was simulated with 10 million dark matter particles and force softening of 1 kpc. Roughly a factor of 107 times the computational cost in a timescale of 30 years - an increase in speed that arises from both algorithmic and hardware developments. Four major development have lead to this performance increase: grid based codes or treecodes reduce the work of long range force calculations, multistepping saves moving all the particles on the same short timestep as the handful of particles in dense regions, faster cpu's, parallel codes can scale up to 90% efficiency on large numbers of nodes. Figure 3 shows the ``N'' versus year plot for several cluster simulations over the last 38 years.
|
Figure 3. A selection of dark matter only cluster simulations. I have attempted to plot the number of particles within the final virial radius against the publication year. The dashed line illustrates ``Moore's law'' (named after Gordon Moore who founded Intel and noted the rapid increase in the density of transistors on a silicon chip with time) which roughly equates to a doubling of cpu speed every three years. This type of plot suffers from many biases and is not meant to be taken seriously. The fact that recent simulations lie on this curve does not imply that algorithmic advances are not important - quite the opposite since the force softening is reduced typically in proportion to N-1/3 which requires more computational work. |
We now have a host of new observational tests of the hierarchical structure formation paradigm that include: the extent of galactic halos in clusters or satellites in galactic halos, the orbital distribution of cluster/satellite galaxies, the number of satellites as a function of their circular velocity or mass, the spatial and velocity distribution of satellites, the central density profiles of clusters and galaxies are close to r-1.5. Unfortunately, observational tests of these model predictions on cluster scales are non trivial and just a few exist in the literature (Tyson etal 1998, Natarajan etal 1998, Smith etal 2000).