Copyright © 1991 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1991. 29:
325-362 Copyright © 1991 by Annual Reviews. All rights reserved |
2.2.2. THE FLATNESS PROBLEM
A comparison with the present epoch gives, assuming k
Since, as t -> 0, |
The present astronomical observations place
Stated differently, had this fine-tuning not occurred, the universe
would have contracted back to a = 0 (for k = 1) or
diffused to a =
The flatness problem can be posed alternatively as follows. The
entropy density of photons at thermal equilibrium at temperature T is
given by (4  in Eq. 2 leads
to the relation
in Eq. 2 leads
to the relation
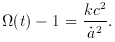
 0,
0,
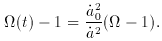
 | ->
| ->
 , the convergence of
, the convergence of  (t) onto the flat value
1 is very rapid as we approach t = 0. Expressed as a function of
temperature, this relation becomes
(t) onto the flat value
1 is very rapid as we approach t = 0. Expressed as a function of
temperature, this relation becomes
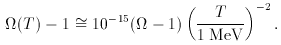
 within a range of 0.1 to
2. Thus |
within a range of 0.1 to
2. Thus | - 1| is of order
unity. At the GUTs epoch, however, with a
- 1| is of order
unity. At the GUTs epoch, however, with a  t1/2, we have
t1/2, we have  2
2  t-1. Putting in numbers, we find that
t-1. Putting in numbers, we find that  02 /
02 /  2
2  10-48. In other words, |
10-48. In other words, | (t) - 1| is extremely fine-tuned to value zero.
(t) - 1| is extremely fine-tuned to value zero.
 (for k = -1) long before the present epoch. In the absence of any
physical mechanism, this fine-tuning has to be imposed ad hoc at the
GUTs epoch in the standard model.
(for k = -1) long before the present epoch. In the absence of any
physical mechanism, this fine-tuning has to be imposed ad hoc at the
GUTs epoch in the standard model.
 / 45)
T 3. Since a
/ 45)
T 3. Since a  T-1, the total entropy in a proper
volume, v
T-1, the total entropy in a proper
volume, v  a3, in an expanding universe is conserved. Its present
value in the observable region is about 1085. Such a large
value for a dimensionless conserved quantity is hard to explain.
a3, in an expanding universe is conserved. Its present
value in the observable region is about 1085. Such a large
value for a dimensionless conserved quantity is hard to explain.