Copyright © 1991 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1991. 29:
325-362 Copyright © 1991 by Annual Reviews. All rights reserved |
The source term for Einstein's equations is any conserved stress
tensor. If this stress tensor is isotropic with strength  (corresponding to an equation of state p = -
(corresponding to an equation of state p = -  c2 = -
c2 = -
 , implying
either pressure or density to be negative), then the quantity
, implying
either pressure or density to be negative), then the quantity  is
called the cosmological constant. Such a term was originally
postulated by Einstein and has an interesting history (see e.g.
124).
is
called the cosmological constant. Such a term was originally
postulated by Einstein and has an interesting history (see e.g.
124).
The value of such a constant is severely constrained by cosmological
considerations. Since  contributes
contributes 
 = (8
= (8  G
G  /
3H02) to the critical
density, one can safely conclude (in spite of any astronomical
uncertainties!) that
/
3H02) to the critical
density, one can safely conclude (in spite of any astronomical
uncertainties!) that
As discussed below, this small value is a deep mystery.
To begin with, nothing prevents the existence of a
The surprise in the smallness of |
Quantum field theory provides a wide variety of contributions to
and
will give the same effects, though they differ by the constant term
(µ4 / 4
Finally, one should not forget that the ``zero-point energy'' of
quantum fields will also contribute to gravity
(91,
131). Each degree
of freedom contributes an amount
where kmax is an ultravioqlet cut-off. If we take
general relativity to
be valid up to Planck energies, then we may take kmax
If we assume that all the contributions are indeed there, then they
have to be fine-tuned to cancel each other, for no good reason. Before
the entry of GUTs into cosmology, we needed to worry only about the
first and last contribution, both of which could be tackled in an ad
hoc manner. One arbitrarily sets
Several mechanisms have been suggested in the literature to make the
cosmological constant zero: supersymmetry
(26,
79,
80,
135),
complicated dynamical mechanisms
(37,
97,
110,
F. Wilczek and A. Zee,
unpublished), probabilistic arguments from quantum gravity
(12,
24,
53,
89),
and anthropic principle
(123)
are only a few of them. None of
these seems to provide an entirely satisfactory solution. A somewhat
different approach in which scale invariance was used to set
The smallness of the cosmological constant is probably the most
important single problem that needs to be settled in cosmology. We
have no idea as to what this mechanism is, but if it is based on some
general symmetry consideration, it may demand vanishing of 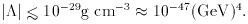
 -term (say,
-term (say,  0)
in Einstein's equations (as postulated by him). This will make the
gravitational part of the Lagrangian dependent on two fundamental
constants
0)
in Einstein's equations (as postulated by him). This will make the
gravitational part of the Lagrangian dependent on two fundamental
constants  0 and
G, which differ widely in scale; the dimensionless
combination made out of these fundamental constants, (G
0 and
G, which differ widely in scale; the dimensionless
combination made out of these fundamental constants, (G / c3)
/ c3) 0, has a
value less than 10-126!
0, has a
value less than 10-126!
 | is mainly due to the following:
We do not know of any symmetry mechanism that requires it to be
zero. In fact, we know of several independent, unrelated phenomena
that contribute to
| is mainly due to the following:
We do not know of any symmetry mechanism that requires it to be
zero. In fact, we know of several independent, unrelated phenomena
that contribute to  . To
produce such a small
. To
produce such a small  , these
terms have to be fine-tuned to a bizarre accuracy.
, these
terms have to be fine-tuned to a bizarre accuracy.
 . For example, consider a
scalar field with a potential V (
. For example, consider a
scalar field with a potential V ( ). The
particle physics predictions do not change (except possibly in
theories with exact supersymmetry, a condition not realized in nature)
if we add a constant term V0 to this potential. A
potential like
). The
particle physics predictions do not change (except possibly in
theories with exact supersymmetry, a condition not realized in nature)
if we add a constant term V0 to this potential. A
potential like
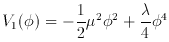
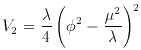
 ), but such a shift in the energy-density will contribute
to
), but such a shift in the energy-density will contribute
to  .
According to currently accepted scenarios, the value of this constant
changes in every phase transition by E4 where E
is the energy scale at
which the phase transition occurs: at the GUTs transition, it is
1056
(GeV)4; at the Salam-Weinberg transition, it changes by
1010 (GeV)4.
These are enormous numbers compared to the present value of 10-47
(GeV)4. How a physical quantity can change by such a large magnitude
and finally adjust itself to be zero at such fantastic accuracy is not
clear.
.
According to currently accepted scenarios, the value of this constant
changes in every phase transition by E4 where E
is the energy scale at
which the phase transition occurs: at the GUTs transition, it is
1056
(GeV)4; at the Salam-Weinberg transition, it changes by
1010 (GeV)4.
These are enormous numbers compared to the present value of 10-47
(GeV)4. How a physical quantity can change by such a large magnitude
and finally adjust itself to be zero at such fantastic accuracy is not
clear.
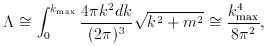
 1019 GeV and
1019 GeV and  will be 1076
(GeV)4.
will be 1076
(GeV)4.
 0 = 0 in the Lagrangian defining
gravity and tries to remove the zero-point contribution by complicated
regularization schemes. (Neither argument is completely water-tight
but both seem plausible.) With the introduction of GUTs and
inflationary scenarios however, the cosmological constant becomes a
dynamical entity and the situation becomes more serious. Notice that
it is precisely the large change in the V (
0 = 0 in the Lagrangian defining
gravity and tries to remove the zero-point contribution by complicated
regularization schemes. (Neither argument is completely water-tight
but both seem plausible.) With the introduction of GUTs and
inflationary scenarios however, the cosmological constant becomes a
dynamical entity and the situation becomes more serious. Notice that
it is precisely the large change in the V ( ) that leads to a
successful inflation; it has to be large to inflate the universe and
change to a small value in the end for a graceful exit from the
inflationary phase.
) that leads to a
successful inflation; it has to be large to inflate the universe and
change to a small value in the end for a graceful exit from the
inflationary phase.
 = 0 was
provided by the conformal theory of gravity
(61).
= 0 was
provided by the conformal theory of gravity
(61).
 at all
epochs. This can wipe out the entire inflationary picture.
at all
epochs. This can wipe out the entire inflationary picture.