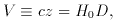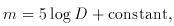© CAMBRIDGE UNIVERSITY PRESS 1983, 1993
| |
1.8 Expansion of the Universe
We now come to the observations that Launched modern cosmology. Between 1912 and 1925, V.M. Slipher measured the shifts in the spectra of more than 20 objects that later turned out to be galaxies. Slipher was surprised that all shifts were towards the red end. Later, E. Hubble and M. Humason extended Slipher's list of observations to more galaxies and to the brightest cluster galaxies. An example of the pattern that emerged when the redshift was plotted against distance of a galaxy is shown in Figure 1.21 (see also Figure 1.22).
If all galaxies seen are equally bright, then the magnitudes are proportional to the logarithm of distances. Thus the straight line drawn through the cluster of points corresponds to the linear relation
where D
is the distance of the galaxy and z its redshift. If the redshift were
due to the Doppler effect, then we could ascribe to the galaxy a
velocity of recession V relative to us. (Since z << 1 in
the observations of Hubble and Humason, and the Newtonian Doppler shift
formula is valid.) The constant H0 is now known as
Hubble's constant.
If instead of plotting z against the distance D, log
z is plotted
against the apparent magnitude m of the galaxy, then another
straight-line relation shows up (see section 3.6 for a definition of
apparent magnitude).
For,
and (1.3) implies
Since the distances of remote galaxies are determined through their
apparent magnitudes (as discussed in Chapter 9), (1.5) is the practical
form of Hubble's linear relation (1.3).
The relation (1.3) is called Hubble's law. It was published as a
linear law by Hubble in 1929, and it caused great excitement. For the
prima facie interpretation of Hubble's law seemed to be that there was a
great explosion in our neighbourhood of the universe from which galaxies
were thrown out. However, the linearity of Hubble's law shows that we
need not consider ourselves in any special position in the universe. If
we viewed the population of galaxies from any other galaxy, we would
notice the same Hubble's law. The combination of this fact with the
homogeneity and isotropy of the distribution of the population of
galaxies suggests a highly regular structure of the universe.
Imagine a piece of dough with self-raising flour being baked in the
oven, and suppose we have spread caraway seeds uniformly throughout the
dough. As the dough bakes it expands, and the seeds move away from each
other. The phenomenon of the recession of galaxies might be looked upon
in the same light. They are points embedded in space that is expanding.
This notion of galaxies embedded in expanding space led to the concept
of the expanding universe.
The rate of expansion is characterized by Hubble's constant. Hubble
obtained a value for H0 in the neighbourhood of 530 km
s-1 Mpc-1. (Note
that these units arise because H0 is velocity divided
by distance. The dimensions of H0-1 are
simply those of time.) As we will discuss in
section 9.2, Hubble had grossly underestimated the galactic distances,
with the result that his value of H0 was too high. The
value of H0 is
now believed to lie in the range of 50 to 100 km s-1
Mpc-1. We will
write it as 100 h0 km s-1 Mpc-1,
where h0 lies between 0.5 and 1. Notice
that if we assume Hubble's law we can estimate the distance of an
extragalactic object from its redshift.