One of the most interesting subjects in the study of AGNs is the
question of the supply
of mass that fuels them, thus `feeding the monster'
(Gunn 1979).
For instance, a black hole with mass 108.5
M
with
luminosity 0.1 LE, and if its efficiency of mass
conversion is 0.1, consumes about 0.7
M
y-1. If the mass supply is available and the
two factors remain constant, its mass will increase exponentially on a
time scale of
4.4 x 108 y. However, the mass supply must be available at
the accretion disk, with a
radius perhaps 100 times its Schwarzschild radius, that is about 5 x
1015 cm 
10-3 pc.
This is practically zero on the scale of the galaxy, and to fall that
close to the center,
the mass must lose practically all of the angular momentum it had on the
scale of the
galaxy. Thus the problem of fuelling AGNs is the problem of how mass
arrives at the
accretion disk, close to the black hole, with low angular momentum. Many
different mechanisms have been studied
(Rees 1984).
In recent years considerable observational
evidence has tended to favour interactions between galaxies and mergers
as the main
fuelling mechanism. We will discuss this evidence, and theoretical
calculations related
to it in this section, after reviewing the observational data on the
luminosity function
of AGNs (relative numbers here and now), the presence of black holes in
inactive
galactic nuclei, and the statistics of AGNs in various environments.
7.2. Luminosity functions of AGNs
The luminosity function of Seyfert galaxies means the number per unit
luminosity
interval (or optical absolute magnitude interval) per unit volume. Even
though Seyfert
galaxies are quite luminous, the quantitative information on the
luminosity function
is limited to `here and now', actually to about redshift z
0.03-0.05. The luminosity
function can be derived from a sample that is complete down to a given apparent
magnitude, basically from a census of the objects. For each galaxy the
redshift gives
the distance and hence absolute magnitude, and the limiting magnitude of
the sample
then gives the volume-out to which that galaxy could be observed in the
sample. Its
contribution to the luminosity function is one object in that volume;
the sum of all
the densities derived in this way is the luminosity function.
A good, more recent determination of the luminosity function by this method is by Meurs and Wilson (1984). Their result is that for absolute magnitude MB = -21 and fainter, about 10% of all field galaxies are Markarian galaxies, and approximately 8% of Markarian galaxies between MB = -20 and -21 are Seyferts. But at higher luminosities the fraction that are Seyferts increases rapidly. More luminous than about MB = -22.5, nearly all field galaxies are Markarian galaxies and almost all of them are Seyfert galaxies! (These absolute magnitudes are based on an assumed Rubble constant H0 = 50 km s-1 Mpc-1; for any other value they can be scaled accordingly.) Integrated over their whole range of absolute magnitude, -24 < MB < -19, Seyfert galaxies are about 1.1% of all galaxies in that interval. This luminosity function converges smoothly with the luminosity function of QSOs at brighter absolute magnitude.
Furthermore, the separate luminosity functions of Seyfert 1 and 2 galaxies can be found in the same way. The Meurs and Wilson (1984) work shows the Seyfert 1s to have a weak maximum at MB = -21, and the Seyfert 2s at MB = -20. Essentially all the high-luminosity objects are Seyfert 1s. According to these luminosity functions the numbers of Seyfert 1s and 2s per unit volume are the same, but to a given apparent magnitude the number of Seyfert 1s is about twice the number of Seyfert 2s.
However, as noted in section 2.8, the
Markarian survey, from which all of
Meurs and Wilson's
(1984)
sample was drawn, is seriously incomplete in Seyfert 2 galaxies. Hence
the relative number of Seyfert 2s, and their luminosity function, are
underestimated.
Probably the best area for Seyfert galaxy statistics is the
Wasilewski (1983)
field, covering 825 square degrees at the North Galactic Pole, searched
for emission-line galaxies
down to mB
17, and is believed to be complete to mB = 15.7.
Osterbrock and Shaw
(1988)
obtained slit spectra of all the Seyfert-galaxy candidates, as well as many of
the other emission-line galaxies, and found the observed numbers of
Seyfert 1 + 1.5 to
Seyfert 1.8 + 1.9 to Seyfert 2 to be 4; 2; and 9
respectively. Correcting for the higher
luminosity of the Seyfert 1s, this corresponds to relative space
densities (luminosity
functions integrated over absolute magnitude) 0.12 : 0.10 : 0.78, with
large uncertainties
because of the small number of objects. Probably all the Seyfert 1.5s
and half the
Seyfert 1.8s and 1.9s would be classified Seyfert 1, the rest of the
Seyfert 1.8s and 1.9s
as Seyfert 2s, if only these two types were used. Thus a large upward
correction to the
number density of Seyfert 2 galaxies from the Meurs and Wilson
luminosity function
is required, to approximately five times the number of Seyfert 1s. This
ratio has been
only slightly changed by the discovery of one more Seyfert 1 and one
more Seyfert 2 in the Wasilewski field by
Bothun et al
(1989).
A similar ratio, 5.3 ± 2.4, has been derived by
Salzer (1989)
from a complete (magnitude-limited) sample of emission-line
galaxies in a larger field from the University of Michigan (UM) survey.
Edelson (1987),
in a complete magnitude-limited sample (mB
14.5) based on the CfA survey, found
25 Seyfert 1 galaxies and 23 Seyfert 2, corresponding to a ratio of
space densities of
Seyfert 2s to 1s of about 2.6, rather than 4.9 as in the Wasilewski
field. In either case,
since the Seyfert 1s are much more nearly complete in the Meurs and
Wilson sample,
the fraction of field galaxies brighter than MB = -19
which are Seyfert 1 is about 1%, and Seyfert 2, about 3 to 5%.
In a very interesting recent study, Spinoglio and Malkan (1989) have used the 12 µm IRAS measurements to form a complete sample of AGNs. The flux at this wavelength, they argue, is least affected by dust absorption and emission, and thus is best correlated with the bolometric luminosity of the AGN. The resulting luminosity functions for Seyfert 1 and 2 galaxies agree well with those derived from the CfA survey. Approximately 20% of the galaxies in the flux-limited 12 µm sample contain active nuclei. Thus this appears to be an extremely efficient technique for discovering AGNs.
On any evolutionary picture in which Seyfert 1s evolve into Seyfert 2s, or vice versa (or both, which has been observed nearly to happen, on scales of a few months, in NGC 4151 by Penston and Perez (1984)) the relative fractions are proportional to the relative times spent in each form. If all galaxies went through the Seyfert stages, they would spend 1% of their (observable) lives as Seyfert 1s, say 4% as Seyfert 2s, and the rest as field galaxies. If only some galaxies did so, the fraction of their lifetimes they spent as `field galaxies' would be smaller, and as Seyferts correspondingly larger.
On the other hand, if all Seyfert 2s had hidden BLRs, visible only from a cone centered about an axis, the half angle of this cone would be about 40°, its whole opening 80°, for a representative AGN.
More recently Cheng et al (1985) have discussed the luminosity function of Seyfert 1 (and 1.5) nuclei, which is more significant than that of the galaxies with the nuclei included. They tried to correct for the starlight of the galaxy itself, using available colour and galaxy surface-brightness information. The derived luminosity function agrees reasonably well with that of Meurs and Wilson, when the latter is adjusted to remove approximately the galaxy contribution to the total magnitude. The luminosity function for QSOs (MB < -23) has been determined by Schmidt and Green (1985), based on a colour survey of the entire sky accessible from Palomar (the Palomar-Green or PG survey). The luminosity function for Seyfert 1 nuclei matches up quite well with it around absolute magnitude -23. For rough orientation, the luminosity function is about 10-6 AGNs Mpc-3 mag-1 at MB = -20.5, 10-7 at MB = -22.0, 10-8 at MB = -23.5 and 10-9 at MB = -25.2. For the most luminous absolute magnitude, the space density is very low, the volume surveyed and the light-travel time correspondingly large. Hence assumptions must be made about the evolution of AGNs. This is a fascinating subject, but not at all well determined physically. In fact, understanding QSOs physically so that their rate of formation and evolution can be calculated is the ultimate aim of AGN research.
7.3. Black holes in normal galaxies
To detect a black hole directly is difficult, because its only interaction with the outside world is gravitational. Among stars, the technique is to find a single-lined spectroscopic binary in which the dark companion has a mass greater than the upper limit to a neutron star, and a strong upper limit to its luminosity. In galaxies the procedure is to measure velocities close to the nucleus which require a central point-like mass, rather than the integrated mass density of the stars.
As stated in section 6.4, far-infrared and
high radio-frequency measurements of
gas emission-line velocities less than 1 pc from the center of our
Galaxy suggest the
presence of a black hole of mass about 5 x 106
M. This
interpretation is not certain,
however, for it depends on assumptions which, though reasonable, are not
unique as
to the unobserved velocity components normal to the line of sight
(Genzel and Townes
1987).
In other galaxies the technique is to measure the line widths and
projected velocity
field in the integrated stellar absorption-line spectrum very near the
nucleus. Only the
nearest galaxies can be investigated, and the angular resolution set by
seeing is the
chief observational limitation. Results to date include probable
detection of a black hole of mass ~ 5 x 107
M in M 31, and
~ 8 x 106
M in M 32. The
inner parts of the
nuclei of both these nuclei show rapid rotation, and an increase in
velocity dispersion
at their centers. Again, the interpretation of the observed data is not
certain, but
the presence of black holes in both these inactive galactic nuclei seems
quite likely
(Dressler and
Richstone 1988,
Kormendy 1988).
7.4. Clusters, groups, and neighbour galaxies
It has long been known that the relative number of AGNs (with respect to `normal' galaxies) is much smaller in rich clusters of galaxies than in the general field. A very good summary is given by Dressler et al (1985). From a relatively homogeneous body of spectra of galaxies in 14 rich clusters (average z = 0.04) and of field galaxies, they found the frequency of AGNs to be only approximately 1% in the cluster sample, compared with approximately 5% in the field galaxies. The clusters on the average are well known to have earlier-type (gas-poor) galaxies (typically E and SO) than the field and, as previously noted, Seyfert galaxies are more frequent among Sa and Sb spirals. However, this only partly accounts for the difference in frequency of AGNs between clusters of galaxies and the field; much of this difference must result from the differing environments. However, a relatively few clusters contain a higher frequency of AGNs, the best example is 3C 295 in which about 10% of the most luminous galaxies (top three magnitudes) are AGNs (Dressler and Gunn 1983).
These statistics strongly suggest that the gravitational interactions of galaxies in clusters, and their interaction with the intergalactic medium in clusters, does not deliver mass to the nuclei. Probably the intergalactic medium sweeps some interstellar gas out of the cluster galaxies, reducing the amount available as fuel (Gisler 1978). The large relative velocities of galaxies in clusters also reduce the strength of their interactions.
From counts of galaxies in the fields of Seyfert galaxies, Petrosian (1982) found that Seyferts do occur in looser clusters, in the same proportion as in the general field. However they tend to avoid the denser central regions of such clusters. In addition Seyfert 2s tend to occur more frequently in loose clusters than Seyfert 1s.
At the other extreme, it seems very well established that AGNs occur much more
frequently in galaxies which have a nearby `companion' galaxy. (The word
in this
context is not meant to imply that the `neighbour' galaxy is in a
long-term bound
orbit, as in the case of stars, but that it is close enough to interact
gravitationally. If
this is the case, and the relative motion is slow enough, the orbit
tends to decay in
only a few periods and the two galaxies merge or interact strongly.) The
tendency
of Seyferts to occur in pairs or interacting galaxies has long been known
(Adams 1977,
Vorontsov-Velyaminov
1977).
Dahari (1984)
investigated this hypothesis
quantitatively in a survey of a well-defined redshifted-limited sample
of Seyfert galaxies.
With a quantitative definition of a close companion in terms of
projected distance
and redshift, he found the fraction of Seyferts with companion galaxies
to be about
15%, while the upper limit in a comparison sample of field galaxies was
only 3% with
companions. The overabundance of very close companions of
comparable size to the Seyferts was even greater.
Fuentes-Williams and
Stocke (1988)
did not confirm this
result, finding only very marginal evidence that Seyferts have an excess
of `companions'
of comparable size. The results of both studies are quite sensitive to
the correction for
background projected galaxies (`optical companions' in the terminology
of double-star
astronomy). Dahari used a procedure based on the local background
density, while
Fuentes-Williams and Stocke used average background
corrections. Dahari's sample
contained about twice as many Seyfert galaxies as Fuentes-Williams and
Stocke's, and
also has a smaller redshift limit, z
0.03 compared with z
0.05.
The most recent survey, by MacKenty (1989) based on a sample of 51 Seyfert galaxies with z < 0.043 and an approximately equal number of non-Seyfert Markarian galaxies, confirms Dahari's result. Seyferts are more likely than field galaxies to have close `companions'. However, the non-Seyfert Markarian galaxies, basically starburst galaxies or galaxies in which star formation is now going on strongly, are equally likely as Seyferts to have companions. Many Seyfert galaxies also have star formation going on in them, others do not. Evidently there is a strong connection between these two processes, which strengthens the idea that fuelling by perturbations of interstellar gas, which is known to be important in star formation, is also involved in AGNs.
One reason for the discrepancy with the results of Fuentes-Williams and Stocke is that their sample of Seyfert galaxies is drawn from relatively early published lists of these objects, which, as explained in section 2.8, are relatively deficient in Seyfert 2s. Dahari's and MacKenty's samples are drawn from more recent catalogues, whose contents are more nearly representative of the total population of Seyfert galaxies. Dahari did not treat Seyfert 1s and 2s separately in his statistics, but MacKenty (1989) did, and found the Seyfert 2s more likely to have companions than Seyfert 1s. Despite the small sizes of the samples, the result appears to be significant. This same result, that Seyfert 2 galaxies are more likely to have companions than Seyfert 1s, was first found by Petrosian (1982). This, and their greater prevalence in loose clusters, are two of the few morphological differences known between these spectroscopically-defined classes, and thus one of the few counterarguments to the hypothesis that both are identical types of objects seen from different orientations. Thus the sample Fuentes-Williams and Stocke used, being deficient in Seyfert 2s, was also deficient in companions.
It has also long been known that many Seyfert AGNs are in interacting systems, galaxies in which the gravitational interaction with their companions is visible by their perturbed structure. Adams (1977) and Vorontsov-Velyaminov (1977) called attention to this observational result, and many quantitative statistical studies since then have confirmed it (Kennicutt and Keel 1984, Keel et al 1985, Dahari 1985, MacKenty 1990). In general, all these studies show that an excess of interacting galaxies have AGNs, but strongly interacting systems (such as the extreme Vorontsov-Velyaminov and Arp objects) tend not to have AGNs. These strongly interacting systems have strong star formation going on, as do many of the less strongly interacting ones.
Many morphological studies of low-redshift QSOs also show direct evidence of interaction in the morphology of the `fuzz' or host galaxy in which they are found (Hutchings 1983, Hutchings et al 1984).
Finally, several so-called `multiple-nuclei' Seyfert galaxies are known, which appear to be close collisions in progress. Some of them may be actual mergers. Some of them show apparent tidal tails. Other objects, in which only an apparently single nucleus is seen, have strong tidal tails and apparently contain two nuclei too close to be resolved. The bright, peculiar Seyfert 1 galaxy Mrk 231, appears spectroscopically and morphologically to be a recently merged system. These and other observational evidence for the interaction interpretation of AGNs are well discussed by Fricke and Kollatschny (1989).
The observational data of the last section strongly suggest that
interactions of galaxies
are an important mechanism for providing fuel to the central accretion
disk in AGNs.
Any interaction will introduce a non-axisymmetric perturbation. These
perturbations,
by breaking down conservation of angular momentum for individual orbits,
can allow
interstellar gas either originally present in the galaxy or acquired in
the interaction,
to fall inward to distances of order 1 kpc from the nucleus
(Norman and Silk 1983).
The fact that most AGNs are in spirals, gas-rich objects, suggests that
interstellar gas
does provide the fuel. As gas accumulates at this distance scale,
presumably in the
form of molecular clouds, instabilities in this self-gravitating disk,
with cloud-cloud
(dissipative) collisions can lead to an instability that allows the gas
to fall inward on a
relatively short time scale. Numerical examples worked out by
Lin et al (1988)
suggest
time scales of order several x 108 y for black holes of mass
107-108
M. Although
these authors consider that this instability can take the gas all the
way in to distances
of order 1 pc, a more attractive possibility has been put forward by
Hernquist (1989a).
It is that on the scale of 100 pc the increased density in the gas can
trigger a burst of
star formation. Observationally, such starbursts are seen in many AGNs,
as previously noted, as has been particularly emphasized by
Weedman (1983).
From this stage
the remaining gas will contract to the center more rapidly as it becomes fully
self-gravitating. At a scale of order 1 pc, if a black hole is present
viscosity will take over
and get the gas into the accretion disk. If not, possibly a dense star
cluster will form, and from it a black hole.
An overall hierarchical set of processes, with several alternative paths from the scale of the galaxy down to the central accretion disk has thus been suggested by Hernquist (1989a). It is shown in figure 8, which can be consulted for a fuller explanation and estimates of many of the relevant time scales. Many details remain to be worked out, but the general ideas that interactions are involved, that several stages, and several alternate processes within each of them are involved, and that star formation is often an important aspect of the AGN phenomenon, are all in good accord with the available observational results. Another discussion emphasizing the importance of bars and non-axisymmetric perturbations is the review by Shlosman et al (1990).
|
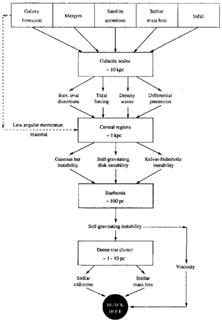
Figure 8. Simple hierarchical model for the origin and fuelling of activity in galactic nuclei. High-angular momentum gas deposited on galactic scales (top of figure) is driven to the central ~ 1 kpc by intermediate processes. Low-angular momentum material settles there directly. Once sufficient gas accumulates there, instabi lities can drive it to the inner ~ 100 pc, triggering a starburst. Continued collapse, as the gas becomes fully self-gravitating, may then form and can fuel a central black hole. (Hernquist 1989a |
Following up an earlier morphological study by Simkin et al (1980), MacKenty (1990) confirmed the widespread prevalence in the Seyfert class of disturbed, interacting or peculiar galaxies. Many of the remainder have bars or rings. In addition, approximately 20 to 25% of the sample he studied had amorphous (or `difficult to classify') structures. Their colours do not agree with those of elliptical galaxies, and they can most simply be interpreted as the remnants of interactions or interactions in the recent past.
Galaxy interactions are complicated to model, and progress in understanding them can only be made with large computers and sophisticated programs. The early calculations of Toomre and Toomre (1972) showed that strongly perturbed systems, similar to those observed, are indeed expected to arise in gravitational interactions between galaxies. The idea that such interactions can deliver mass to the nucleus was made in this paper, in the context of stars rather than gas. Detailed n-body calculations, aimed at interpreting observational data on the statistics of Seyferts with companions, have been made by Byrd et al (1986, 1987). These calculations reproduce semi-quantitatively the association of the strength of the tidal perturbation (Mp / MT) / (p / a)3, where Mp is the mass of the perturbing galaxy, MT the disk plus halo mass of the perturbed galaxy, p the perigalactic distance of the perturber and a the galaxy disk radius, with the presence or absence of nuclear activity. By taking account of projection effects, and possible `companion' galaxies too faint to have been observed, they show that tidal interactions might account for nearly all AGNs. All these calculations are based on an n-body code in which only gravitational interactions are taken into account.
The most recent calculations of Hernquist (1989a, 1989b) treat stars and gas separately, using a hybrid n-body-hydrodynamics code. As these calculations are continued, and made even more sophisticated, it will be possible to test the overall picture described here more thoroughly.