


2.1 Blazar Properties and Relativistic Beaming
The main properties of blazars can be summarized as follows:
 L /
L /  t);
t);
The last property might require some explanation. The term ``superluminal motion'' describes proper motion of source structure (traditionally mapped at radio wavelengths) that, when converted to an apparent speed vapp, gives vapp > c. This phenomenon occurs for emitting regions moving at very high (but still subluminal) speeds at small angles to the line of sight (Rees 1966). Relativistically moving sources ``run after'' the photons they emit, strongly reducing the time interval separating any two events in the observer's frame and giving the impression of faster than light motion.
Analytically, the observed transverse velocity of an emitting blob,
va
=  a
c, is related to its true velocity, v =
a
c, is related to its true velocity, v =  c, and the
angle to the line of sight
c, and the
angle to the line of sight  by
by
It can be shown that if
All these properties are consistent with relativistic beaming, that is
with bulk relativistic motion of the emitting plasma towards the observer.
There are by now various arguments in favor of relativistic beaming in
blazars, summarized for example by
Urry and Padovani (1995).
Beaming has
enormous effects on the observed luminosities. Adopting the usual definition
of the relativistic Doppler factor
with p = 2 +
All this is very relevant to the issue of
where L48 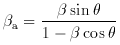
 > 1/
> 1/  2
2  0.7, then for some
orientations superluminal motion (that is,
0.7, then for some
orientations superluminal motion (that is,  a > 1) is
observed. The maximum value of the apparent velocity,
a > 1) is
observed. The maximum value of the apparent velocity,  a, max =
sqrt(
a, max =
sqrt( 2
- 1), where
2
- 1), where  = (1
-
= (1
-  2)-1/2 is the Lorentz
factor, occurs when cos
2)-1/2 is the Lorentz
factor, occurs when cos  =
=
 or sin
or sin  =
=  -1. This
implies a minimum value for the Lorentz factor
-1. This
implies a minimum value for the Lorentz factor  min =
sqrt(
min =
sqrt( a2 + 1). For example, if one detects
superluminal motion
in a source with
a2 + 1). For example, if one detects
superluminal motion
in a source with  a = 5, the Lorentz factor responsible for it
has to be at least 5.1.
a = 5, the Lorentz factor responsible for it
has to be at least 5.1.
 = [
= [ (1 -
(1 -  cos
cos
 )]-1
and applying
simple relativistic transformations, it turns out that the observed
luminosity at a given frequency is related to the emitted luminosity in
the rest frame of the source via
)]-1
and applying
simple relativistic transformations, it turns out that the observed
luminosity at a given frequency is related to the emitted luminosity in
the rest frame of the source via
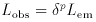
 or 3 +
or 3 +
 respectively in the case of a
continuous jet or a moving sphere
(Urry and Padovani 1995;
respectively in the case of a
continuous jet or a moving sphere
(Urry and Padovani 1995;
 being the spectral
index), although other values are also possible
(Lind and Blandford 1985).
For
being the spectral
index), although other values are also possible
(Lind and Blandford 1985).
For  ~ 0°,
~ 0°,  ~ 2
~ 2  (Fig. 2)
and the observed luminosity can be amplified by factors of thousands (for
(Fig. 2)
and the observed luminosity can be amplified by factors of thousands (for
 ~ 5 and p
~ 3, which are typical values). That is, for jets
pointing almost towards us we can overestimate the emitted luminosity
typically by three orders of magnitude. Apart from this amplification,
beaming also gives rise to a strong collimation of the radiation, which is
larger for higher
~ 5 and p
~ 3, which are typical values). That is, for jets
pointing almost towards us we can overestimate the emitted luminosity
typically by three orders of magnitude. Apart from this amplification,
beaming also gives rise to a strong collimation of the radiation, which is
larger for higher  (Fig. 2):
(Fig. 2):  decreases by a
factor ~ 2 from its maximum value at
decreases by a
factor ~ 2 from its maximum value at  ~ 1/
~ 1/ and
consequently the inferred luminosity goes down by 2p. For
example, if
and
consequently the inferred luminosity goes down by 2p. For
example, if  ~ 5
the luminosity of a jet pointing ~ 11° away from
our line of sight is already about an order of magnitude smaller (for
p = 3) than that of a jet aiming straight at us.
~ 5
the luminosity of a jet pointing ~ 11° away from
our line of sight is already about an order of magnitude smaller (for
p = 3) than that of a jet aiming straight at us.
 -ray emission from blazars.
In fact, if blazars were not beamed, we would not see any
-ray emission from blazars.
In fact, if blazars were not beamed, we would not see any  -ray photons
from them! The qualitative explanation is relatively simple: in sources as
compact as blazars all
-ray photons
from them! The qualitative explanation is relatively simple: in sources as
compact as blazars all  -ray photons would be absorbed through
photon-photon collisions with target photons in the X-ray band. The end
product would be electron-positron pairs. But if the radiation is beamed then
the luminosity/radius ratio, which is the relevant parameter, is smaller by a
factor
-ray photons would be absorbed through
photon-photon collisions with target photons in the X-ray band. The end
product would be electron-positron pairs. But if the radiation is beamed then
the luminosity/radius ratio, which is the relevant parameter, is smaller by a
factor  p+1 and the
p+1 and the
 -ray photons
manage to escape from the source. More formally, it can be shown
(Maraschi et al. 1992)
that the
condition that the optical depth to photon-photon absorption
-ray photons
manage to escape from the source. More formally, it can be shown
(Maraschi et al. 1992)
that the
condition that the optical depth to photon-photon absorption 

 (x) is less than 1 implies (under the
assumption that the X-ray and
(x) is less than 1 implies (under the
assumption that the X-ray and
 -ray photons are
produced in the same region)
-ray photons are
produced in the same region)
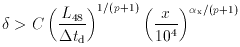
 L
L / (1048 erg/s),
/ (1048 erg/s),  td is the
td is the
 -ray variability
time scale in days (which is used to estimate the
source size), x
-ray variability
time scale in days (which is used to estimate the
source size), x  h
h / me
c2,
/ me
c2,  x is the X-ray
spectral index, and C is a numerical constant
x is the X-ray
spectral index, and C is a numerical constant  10. In other words,
transparency for the
10. In other words,
transparency for the  -ray photons requires a relatively large
Doppler factor for most blazars
(Dondi and Ghisellini 1995)
and therefore relativistic beaming.
-ray photons requires a relatively large
Doppler factor for most blazars
(Dondi and Ghisellini 1995)
and therefore relativistic beaming.