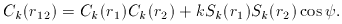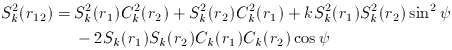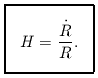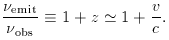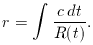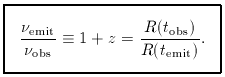© CAMBRIDGE UNIVERSITY PRESS 1999
| |
3.1 The Robertson-Walker Metric
To the relativist, cosmology is the task of finding solutions to Einstein's field equations that are consistent with the large-scale matter distribution in the universe. Modern observational cosmology has demonstrated that the real universe is highly symmetric in its large-scale properties, but the evidence for this was not known at the time when Friedmann and Lemaître began their pioneering investigations. Just as Einstein aimed to write down the simplest possible relativistic generalization of the laws of gravity, so cosmological investigation began by considering the simplest possible mass distribution: one whose properties are homogeneous (constant density) and isotropic (the same in all directions).
ISOTROPY IMPLIES HOMOGENEITY
For isotropy, not only must
Now, as was discovered by Slipher in the 1920s, we do in fact see such
an isotropic recession about us; what does it tell us about the universe?
It is easy to produce an isotropic velocity field: just set off an
explosion that scatters debris in all directions with a range
of speeds v. If the amount of matter involved were too small
for self-gravity to be important, then the distance travelled
by a piece of debris would be just vt and an observer left
in the centre would inevitably see an isotropic distribution of
objects with a recessional velocity proportional to their
distance. However, most scientists believe that it is not
reasonable to adopt a cosmological model in which the universe is
simply a joke played for the benefit of mankind.
This attitude is encapsulated in the Copernican principle,
which states that humans are not privileged observers. Although
obviously false on a local scale (a point selected at random would
be most unlikely to lie so close to a star), there is no reason
why our existence should depend on special features of
the large-scale appearance of the universe. It is therefore a
reasonable supposition that, if the universe appears isotropic
about our position, it would also appear
isotropic to observers in other galaxies; the term
``isotropic'' is therefore often employed in cosmology as a shorthand for
``isotropic about all locations''.
This is a crucial shift in meaning, for the properties of
such a universe are highly restricted.
In fact, given only two points (A and B) from which conditions appear
isotropic, we can prove that they must be homogeneous
everywhere. Construct a sphere about A, on which the density has a constant
value; considering the intersection of this sphere with similar ones
centred on B shows that the density must be constant everywhere within
the sphere, which can then be made as large as we desire
(figure 3.1).
Observationally, this may seem rather abstract, since it is not easy
to verify isotropy from another's viewpoint.
However, a universe that is isotropic about one point and which
is homogeneous has to be isotropic in the general sense.
Consider the expansion: since
Having chosen a model mass distribution, the next step is to
solve the field equations to find the corresponding metric.
Since our model is a particularly symmetric one, it is
perhaps not too surprising that many of the features of the
metric can be deduced from symmetry alone - and indeed will
apply even if Einstein's equations are replaced by something
more complicated. These general arguments were put forward
independently by H.P. Robertson and A.G. Walker in 1936.
COSMOLOGICAL TIME
Here, we have used the equivalence principle to say that the
proper time interval between two distant events would
look locally like special relativity to a fundamental observer on the
spot: for them, c2 d
Because of spherical symmetry,
the spatial part of the metric can be decomposed into a
radial and a transverse part (in spherical polars,
d
To get some feeling for the general answer, it should help to
think first about a simpler case: the metric on the surface of
a sphere. A balloon being inflated is a common popular analogy
for the expanding universe, and it will serve as
a two-dimensional example of a space of constant curvature. If we call the
polar angle in spherical polars r instead of the more usual
It is possible to convert this to the metric for a 2-space
of constant negative curvature by the device
of considering an imaginary
radius of curvature, R -> iR. If we simultaneously
let r -> ir, we obtain
These two forms can be combined by defining a new radial
coordinate that makes the transverse part of the metric look Euclidean:
where k = +1 for positive curvature and k = -1 for
negative curvature. This
argument is hardly a proof that spaces of constant negative curvature
exist and can be justified only by a fuller treatment.
However, it does give a feeling for the meaning of the
final result. Indeed, the equation we have just written is in fact
the exact form of the spatial part of the
Robertson-Walker metric, which applies in any
number of dimensions. The fact that we can obtain the correct answer
using a 2-space is not so surprising in retrospect, because of
isotropy: we only need consider the non-Euclidean nature of
the geometry in a plane to determine the functions f and g.
It is clear that this metric nicely incorporates the idea of
a uniformly expanding model with no centre.
For small separations, where space is Euclidean, we have
a simple scaling-up of vector separations: x (t)
AN INFORMAL DERIVATION
where the constant of proportionality could have either sign.
Apart from the Euclidean case, A = 0, there are thus two possible
geometries:
If we impose the boundary condition
The conclusion of this argument is that
an isotropic universe has the same form for the
comoving spatial part of its metric as the surface of a
sphere. This is no accident, since it it possible to
define the equivalent of a sphere in higher numbers of
dimensions, and the form of the metric is always the same.
For example, a 3-sphere embedded in
four-dimensional Euclidean space would be defined as
the coordinate relation x2 + y2 +
z2 + w2 = R2.
Now define the equivalent of spherical polars and write
w = R cos
which is the Robertson-Walker metric for the case of
positive spatial curvature.
This k = +1 metric describes a closed universe,
in which a traveller who sets off along a trajectory
of fixed
NOTATION AND CONVENTIONS
and its cosine-like analogue, which will be useful later,
The metric can now be written in the preferred form that we shall use
throughout:
The most common alternative is to use a different definition of
comoving distance, Sk (r) -> r, so that the
metric becomes
There should of course be two different symbols
for the different comoving radii, but each is
often called r in the literature, so we have to
learn to live with this ambiguity; the presence of terms like
Sk (r) or
1 - kr2 will usually indicate which convention is being used.
Alternatively, one can make the scale factor dimensionless, defining
so that a = 1 at the present. In this case, the metric becomes
where A is the constant of proportionality from Scheuer's argument,
which is equal to R0, the current value of R
(t). We shall generally
use the metric in the form with dimensionless comoving distances. However,
it is important to note that cosmologists tend to use the term
``distance'' as meaning comoving distance unless otherwise
specified, usually in units of Mpc:
this means that one generally deals with the combination
R0 r.
Other forms of the metric are encountered less commonly; in
particular, the rarely used isotropic form is
There is, however, one other modification of some
importance; this is to define the conformal time
which allows a factor of R2 to be taken out of the metric.
This is a special case of a conformal transformation in
general relativity, such transformations correspond to
gµ
COMOVING SEPARATION
This can be recast in terms of the more usual
Sk(r) via Sk2 = (1 -
Ck2) / k:
For a flat universe (k = 0), this goes over to the
cosine rule, as expected.
To see how complicated a non-intuitive derivation of this
result can become, see Osmer (1981).
THE REDSHIFT
At large separations where spatial curvature becomes important, the
concept of radial velocity becomes a little more slippery - but in any
case how could one measure it directly in practice? At small
separations, the recessional velocity gives the Doppler shift
This defines the redshift z in terms of the
shift of spectral lines. What is the equivalent of this
relation at larger distances? Since photons travel on
null geodesics of zero proper time, we see directly from the metric that
The comoving distance is constant, whereas the domain
of integration in time extends from temit
to tobs; these are the times of emission and reception
of a photon. Photons that are emitted at later times
will be received at later times, but these changes
in temit and tobs cannot
alter the integral, since r is a comoving quantity.
This requires the condition
dtemit /
dtobs= R (temit) /
R(tobs), which
means that events on distant galaxies time-dilate
according to how much the universe has expanded since the
photons we see now were emitted. Clearly (think of events
separated by one period), this dilation also applies
to frequency, and we therefore get
In terms of the normalized scale factor a (t) we have
simply a (t) = (1 + z)-1.
Photon wavelengths therefore stretch with the universe,
as is intuitively reasonable; see figure 3.3.
This is the only correct interpretation of the redshift
at large distances; it is common but misleading to convert
a large redshift to a recession velocity using the special-relativistic
formula 1 + z = [(1 + v/c) / (1 - v/c)]1/2.
Any such temptation should be avoided - it is only valid
in a universe with zero matter density [problem 3.4].
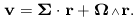
 vanish, but all the principal values of the shear tensor
vanish, but all the principal values of the shear tensor
 must be equal.
Thus, the only allowed velocity field on a local scale is expansion (or
contraction) with velocity proportional to distance:
must be equal.
Thus, the only allowed velocity field on a local scale is expansion (or
contraction) with velocity proportional to distance:
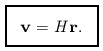
 . v must be a
(homogeneous) constant, v
. v must be a
(homogeneous) constant, v  r; the expansion is
therefore isotropic about every point, since
v1 - v2
r; the expansion is
therefore isotropic about every point, since
v1 - v2  r1 -
r2. We now see how it is possible to
imagine universes that are homogeneous but anisotropic.
For example, a model that expands at different rates along
three principal axes would preserve a homogeneous density,
but the distance-redshift relation could be a function of
direction on the sky.
r1 -
r2. We now see how it is possible to
imagine universes that are homogeneous but anisotropic.
For example, a model that expands at different rates along
three principal axes would preserve a homogeneous density,
but the distance-redshift relation could be a function of
direction on the sky.
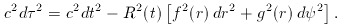
 2 =
c2 dt2 - dx2 -
dy2 - dz2.
Since we use the same time coordinate as they do, our
only difficulty is in the spatial part of the metric:
relating their dx etc. to spatial coordinates centred on us.
2 =
c2 dt2 - dx2 -
dy2 - dz2.
Since we use the same time coordinate as they do, our
only difficulty is in the spatial part of the metric:
relating their dx etc. to spatial coordinates centred on us.
 2 = d
2 = d  2 + sin2
2 + sin2  d
d  2). Distances have
been decomposed into a product of a time-dependent
scale factor R (t) and a time-independent
comoving coordinate r. The functions f and g are
arbitrary; however, we can choose our radial coordinate such
that either f = 1 or g = r2, to make
things look as much like Euclidean space as possible. Furthermore, we can
determine the form of the remaining function from symmetry arguments.
2). Distances have
been decomposed into a product of a time-dependent
scale factor R (t) and a time-independent
comoving coordinate r. The functions f and g are
arbitrary; however, we can choose our radial coordinate such
that either f = 1 or g = r2, to make
things look as much like Euclidean space as possible. Furthermore, we can
determine the form of the remaining function from symmetry arguments.
 , then the element of length on
the surface of a sphere of radius R is
, then the element of length on
the surface of a sphere of radius R is
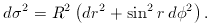
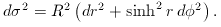
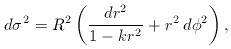
 R (t) x (t0). The same law applies irrespective
of the origin we choose:
x1 (t) - x2 (t)
R (t) x (t0). The same law applies irrespective
of the origin we choose:
x1 (t) - x2 (t)  R (t)
[x1 (t0) - x2
(t0)].
Every fundamental observer with a sufficiently large
ego will conclude that the universe is centred on them.
R (t)
[x1 (t0) - x2
(t0)].
Every fundamental observer with a sufficiently large
ego will conclude that the universe is centred on them.
 is the
comoving separation between two radial light rays and the radial
increment of comoving distance is dr, i.e. we are working
with f = 1 and trying to find
is the
comoving separation between two radial light rays and the radial
increment of comoving distance is dr, i.e. we are working
with f = 1 and trying to find  , which
is equal to g (r) d
, which
is equal to g (r) d . Consider also a
vector that makes an angle
. Consider also a
vector that makes an angle  with one of the light rays.
The effect of non-Euclidean geometry will be to cause
this angle to change by some amount
with one of the light rays.
The effect of non-Euclidean geometry will be to cause
this angle to change by some amount 
 on
parallel transport around the loop. For our present purposes the crucial
step in the argument is to see that isotropy and homogeneity
require that this change must be proportional
to the area of the loop. For example, going around the
loop ABCD twice clearly produces twice the
on
parallel transport around the loop. For our present purposes the crucial
step in the argument is to see that isotropy and homogeneity
require that this change must be proportional
to the area of the loop. For example, going around the
loop ABCD twice clearly produces twice the 
 obtained from one circuit, but from homogeneity this should be the same
as going round two identical loops, ABCD followed by DCEF (the
multiple traversing of the line CD has no effect). Similarly,
one can argue that the effect of any loop should be the sum
of the effects of the sub-loops into which it may be divided.
Given this, it is straightforward to derive
obtained from one circuit, but from homogeneity this should be the same
as going round two identical loops, ABCD followed by DCEF (the
multiple traversing of the line CD has no effect). Similarly,
one can argue that the effect of any loop should be the sum
of the effects of the sub-loops into which it may be divided.
Given this, it is straightforward to derive  , since
, since
 =
=  /
ðr;
/
ðr;

 area therefore becomes
area therefore becomes
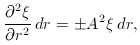
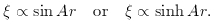
 -> r d
-> r d as r -> 0, then the constants of proportionality may
be found. We end up with the same metric as we obtained from the 2-sphere.
It is possible to give derivations of considerably
greater rigour (consult Weinberg 1972 or Misner, Thorne
& Wheeler 1973 for examples). However, this will suffice here.
as r -> 0, then the constants of proportionality may
be found. We end up with the same metric as we obtained from the 2-sphere.
It is possible to give derivations of considerably
greater rigour (consult Weinberg 1972 or Misner, Thorne
& Wheeler 1973 for examples). However, this will suffice here.
 ,
z = R sin
,
z = R sin  cos
cos
 ,
y = R sin
,
y = R sin  sin
sin  cos
cos
 ,
x = R sin
,
x = R sin  sin
sin  sin
sin
 , where
, where
 ,
,  and
and  are three arbitrary
angles. Differentiating with respect to the
angles gives a four-dimensional vector (dx, dy, dz,
dw), and it is a straightforward exercise to show that the squared
length of this vector is
are three arbitrary
angles. Differentiating with respect to the
angles gives a four-dimensional vector (dx, dy, dz,
dw), and it is a straightforward exercise to show that the squared
length of this vector is
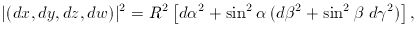
 and
and  will eventually return
to their starting point (when
will eventually return
to their starting point (when  = 2
= 2 ). In this
respect, the positively curved 3D universe is identical
to the case of the surface of a sphere: it is
finite, but unbounded. By contrast, the k = -1 metric
describes an open universe of infinite extent; as
before, changing to negative spatial curvature replaces
sin
). In this
respect, the positively curved 3D universe is identical
to the case of the surface of a sphere: it is
finite, but unbounded. By contrast, the k = -1 metric
describes an open universe of infinite extent; as
before, changing to negative spatial curvature replaces
sin with sinh
with sinh , and
, and  can be made as large as we please without returning to the
starting point. The k = 0 model describes a flat universe,
which is also infinite in extent. This can be thought of as a limit of
either of the k = ± 1 cases, where the curvature scale
R tends to infinity.
can be made as large as we please without returning to the
starting point. The k = 0 model describes a flat universe,
which is also infinite in extent. This can be thought of as a limit of
either of the k = ± 1 cases, where the curvature scale
R tends to infinity.
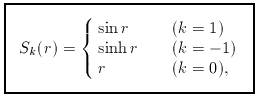
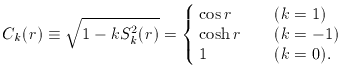
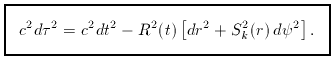
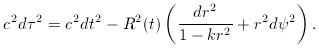
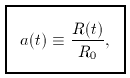
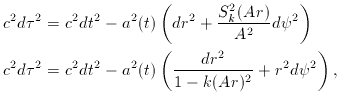
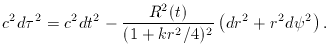
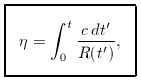
 ->
fgµ
->
fgµ ,
where f is some arbitrary spacetime function. The universe
with k = 0, although certainly possessing spacetime
curvature, is obviously directly related to Minkowski
spacetime via a conformal transformation and so tends to be loosely known as
the ``flat'' model. In fact, the Robertson-Walker
metric turns out to be conformally flat for all values
of k - i.e. a coordinate transformation can always
be found that casts the metric in the form of
the Minkowski metric multiplied by some spacetime function.
,
where f is some arbitrary spacetime function. The universe
with k = 0, although certainly possessing spacetime
curvature, is obviously directly related to Minkowski
spacetime via a conformal transformation and so tends to be loosely known as
the ``flat'' model. In fact, the Robertson-Walker
metric turns out to be conformally flat for all values
of k - i.e. a coordinate transformation can always
be found that casts the metric in the form of
the Minkowski metric multiplied by some spacetime function.
 are not small?
The analogy with a 2-sphere is invaluable in this case, as the answer is
obviously just the spherical cosine rule
(appropriately generalized for positive and negative curvature):
are not small?
The analogy with a 2-sphere is invaluable in this case, as the answer is
obviously just the spherical cosine rule
(appropriately generalized for positive and negative curvature):