3. WHAT MAKES A RADIO-LOUD GALAXY?

Turning now to the infinitely more interesting issue of the population of discrete radio sources, we first review what is known about the causes that lead to enhanced radio emission.

For orientation, it is convenient to give a sketch of the population, ordered according to output. Define P log₁₀ L_{21 cm} / WHz^-1sr^-1; at P 24 we find the classical radio galaxies and quasars, conventionally divided roughly into Fanaroff-Riley (1974) FRII objects like Cygnus A and compact sources such as 3C273. At intermediate powers 23 P 24, we find FRI sources: twin-jet objects such as 3C31, often lurking in clusters. At P 24, we find all the rest of astronomy: `radio-quiet' quasars, starburst galaxies and normal galaxies. We shall be concerned here with the bona-fide radio galaxies having P 23.

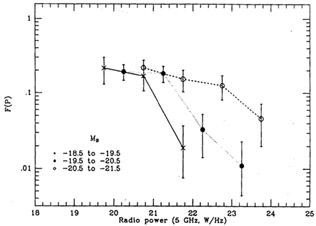
Two outstanding systematics of such galaxies have long been known: they are virtually without exception associated with elliptical/S0 galaxies, and moreover with the massive members of this class. This strong tendency for the probability of strong radio activity to increase with optical luminosity is illustrated in Figure 1. It is however interesting that this figure conceals a more complex behavior noted by Owen & White (1991). They showed that the more powerful FRII sources are actually less likely in the most massive galaxies - i.e. the FR transition shifts to higher radio power at higher optical power. This may indicate an influence of the local density on the ability of a radio jet to remain stable (see Prestage & Peacock 1988). Nevertheless, the increased tendency of more massive galaxies to produce sources of FRI output or above is not in conflict with this interesting discovery.

Figure 1. The differential probability distribution of radio power (for h = 1), for different bins in optical luminosity, taken from Sadler, Jenkins & Kotanyi (1989). Above P = 21 - 22, the probability of radio emission is a very rapidly rising function of optical luminosity.

The rather narrow spread in stellar luminosity for radio galaxies has long been known, and is perhaps best illustrated in the infrared Hubble diagram (Lilly & Longair 1984), which displays an rms of only 0.4 mag. The average absolute magnitude is somewhat brighter than for normal ellipticals. The most direct way of demonstrating this is not to rely on local samples, where powerful radio galaxies are rare, but to turn to a direct comparison at intermediate redshifts. Aragón-Salamanca et al. (1991) give K-band data on ellipticals in the A370 cluster at z = 0.37, from which a Schechter K* = 16.3 for the ellipticals can be determined. Lilly & Longair give K = 15.2 for the mean radio galaxy at this redshift, but this is in a 10" diameter aperture, whereas the cluster data are in 4".8 apertures. The aperture correction at this radius is well modeled by L r^0.5, which introduces a small (0.4 mag.) correction, and leads to the conclusion

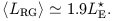
Both the large size of this mean luminosity and its small dispersion may be understood quantitatively as empirical manifestations of the strong trend of radio activity with optical luminosity. If we say that the probability of a galaxy hosting a strong radio AGN is P L_opt, then multiplying this rising power law into the exponential truncation of a Schechter function for the elliptical population as a whole gives roughly the observed mean luminosity and scatter if 4 - 5. This may also go a good deal of the way towards explaining the dominance of elliptical hosts: the L* values for elliptical galaxies tend to be a few tenths of a magnitude brighter than for spirals, a gap which may be stretched to as much as a magnitude if we allow for typical bulge-to-disk ratios to obtain the L* ratios between ellipticals and spiral bulges. We would then predict N_E / N_S 2.5 ~ 10². In other words, massive ellipticals dominate powerful radio sources because only they have the exceptionally deep potential wells needed for the most active radio AGN. This is far from the whole story: first, any possible spiral identifications for powerful radio sources must be more at the 10^-3 level; second, the whole reasoning rests on the strong L trend which remains unexplained. There is still a major puzzle here.

Are there any other distinguishing features of radio galaxies? Almost all other peculiarities can either be traced directly to the effect of the AGN (such as the strong narrow emission lines), or to the peculiarity of high mass already discussed. It would be important to know if there were any systematic differences between those galaxies that turn on a radio active nucleus and those that do not - but there is no strong evidence for any such difference. Various suggestions have been made, but these have usually turned out to be small and subtle effects, whose reality generates controversy.

For example, about a decade ago it was suggested that radio-loud galaxies were redder by about 0.03 mag. in B - V (Sparks 1983), rounder (Disney & Sparks 1984), more rapidly rotating (Jenkins 1984) and in denser environments (Sparks et al. 1984) than their radio-quiet counterparts of the same optical luminosity. Sparks et al. (1984) argued that these trends could be understood within a single picture of fuel gathering in potential wells, with the deeper wells being more successful at generating radio activity. However, in subsequent years the picture has become somewhat more complicated as further data have accumulated. For example, Heckman et al. (1985) found that the suggestion of excess rotation was due to a few incorrect measurements in the compilation used by Jenkins. Smith & Heckman (1989) found a normal distribution of axial ratios and claimed that galaxies were bluer sometimes by as much as 0.2 mag. in B - V. Finally, Smith & Heckman (1990) found environments consistent with those of radio-quiet ellipticals. Part of the problem here may be that any peculiarity may be a function of radio power, so that different studies can yield different answers unless they use the same definition of radio-loudness. Also, the range of properties of radio-quiet ellipticals is large and diverse; misleading conclusions may be reached unless there is a large and complete comparison sample. What is needed is a large sample of radio-loud ellipticals whose properties can be compared to a radio-quiet set matched in optical luminosity and redshift.

In the meantime, claimed peculiarities of radio ellipticals need to be treated with caution. Two properties which are presently in this provisional class are the suggestion that radio ellipticals have low-level isophote distortions indicative of merging (Smith & Heckman 1989), and the question of dynamics. Smith, Heckman & Illingworth (1990) found that radio-loud ellipticals lie on the `fundamental plane' in size/luminosity/velocity dispersion space, but there are some suggestions that they may occupy a different region of the plane - being brighter at a given velocity or size (Sansom, Wall & Sparks 1987; Romanishin & Hintzin 1989). It will be interesting to see how these suggestions hold up. We certainly badly need some clear set of clues as to what triggers these objects.