


2.4.3. Scaling from Clusters to Groups
As an alternative to adding the previous two directly observed
components (warm X-ray emitting gas and cool Lyman- absorbing gas), we can estimate the total plasma in groups
from the assumption that it has the same ratio to dark matter
as in the rich clusters. That is, the scaling used to arrive at the
density parameter in gravitational mass in the field
from spheroid luminosity (eq. [27) readily
generalizes to a scaling estimate of the density parameter in
plasma associated with groups. The product of
equation (18) for the ratio of
plasma to gravitational mass in clusters and
equation (28) for the density parameter in the field yields
absorbing gas), we can estimate the total plasma in groups
from the assumption that it has the same ratio to dark matter
as in the rich clusters. That is, the scaling used to arrive at the
density parameter in gravitational mass in the field
from spheroid luminosity (eq. [27) readily
generalizes to a scaling estimate of the density parameter in
plasma associated with groups. The product of
equation (18) for the ratio of
plasma to gravitational mass in clusters and
equation (28) for the density parameter in the field yields
In a calculation along similar lines
Carlberg et al. (1997)
find a similar result, (
Equation (32) assumes a fair sample of plasma relative
to gravitational mass is assembled and preserved in the great
clusters. If disks were less common in clusters because star
formation has been suppressed, equation (32) would
include baryons in disks in the field, but the correction is
small because the baryon mass in disk stars is small. It is not
thought that cluster cooling flows or winds have seriously
depleted the cluster plasma mass. In a more direct argument
Renzini (1997)
finds that the iron and gas content
of clusters and groups indicate the clusters indeed have close to
the global star formation efficiency, and that the
corresponding enriched gas from groups has been ejected into
intergalactic space, presumably ending up in the form discussed
in Section 2.4.1 and
Section 2.4.2.
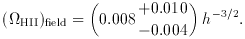
 HII)field = (0.01-0.014)
h-3/2. The central value in equation (32) agrees with
the upper bound from the sum of the more direct estimates in
equations (29) and (31).
HII)field = (0.01-0.014)
h-3/2. The central value in equation (32) agrees with
the upper bound from the sum of the more direct estimates in
equations (29) and (31).