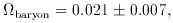5.2. Observable and Unobservable Baryons
A baryon budget must be informed by an understanding of what is reasonable and sensible within standard models for the physics, astronomy, and cosmology. We argue here that these considerations coupled to the observations available now or within reach significantly limit the possibilities for large gaps in the budget.
Chemically Bound Baryons. - Baryons confined by chemical bonds, as in comets, are dark (apart from evaporation) at any significant distance, but we know their contribution to the baryon mass within the luminous parts of normal galaxies is not large: the mass in stars accounts for the dynamics. In the standard cosmology only a small fraction of primordial hydrogen converts to molecular form. Some scenarios envisage a significant mass in molecular clouds (Combes and Pfenniger 1998), but it seems more likely to us that the bulk of this material would by now have formed into stars, as it has in the Galaxy. Baryons could be chemically bound to heavier elements, but it is hard to see how this could be a significant mass component because it would require prodigious heavy element production in closely confined and closed systems and the radiated nuclear binding energy would appear in the background radiation. Besides these arguments we have the direct limits on the density of the plentiful but inert gas helium which would separate from any condensed component. In short, if the existence of a significant mass in intergalactic comets could be established it would contradict the standard cosmological model. The far more credible proposition is that there is not a significant mass fraction in chemically bound baryons.
Dark Galaxies. - The starlight from baryons gravitationally bound in known forms of low surface brightness (LSB) galaxies is only about 15% of our adopted total. Thus if normal galaxies were an adequate guide to their compositions the known LSB galaxies would be insignificant reservoirs of baryons in stars. Discovery of reason to suspect the contrary would be of great interest, of course. The starlight in as yet undetected still lower surface brightness galaxies is constrained by the absolute surface brightness of the sky and fluctuations thereof; a significant contribution already appears unlikely from the smoothness of the background in deep exposures. If measurements indicated the mean optical extragalactic surface brightness is larger than expected from known galaxies it certainly would give reason to think we have missed an important baryon component.
If the surface brightness showed no such anomaly one could still imagine there are dark galaxies with star populations dominated by brown dwarfs, but there are several arguments against the idea. There are high success rates in optical identification of systems of normal galaxies with the objects responsible for gravitational lensing events, for quasar absorption line systems, and for X-ray sources. Even if massive dark galaxies were assumed not to be capable of significant lensing they could contain diffuse baryonic halos, so in this scenario we would need to explain why they do not cause a significant rate of identification failures for quasar absorption lines and X-ray sources. One way assumes the dark galaxies avoid the concentrations of normal galaxies and the associated plasma, so they do not acquire plasma halos, but there are two counter arguments. First, in this picture there surely would be intermediate cases, dim massive galaxies that avoid the normal ones, and there is no evidence of them. Second, the familiar morphology-density relation in observed galaxies goes the other way: gas-rich galaxies prefer lower density environments, gas-poor anemic spirals denser regions.
Dust-Shrouded Stars. - Populations of stars shrouded in dust are constrained by the integrated far infrared background of reradiated starlight, which is observed to have an integrated flux about twice that from optical galaxies as estimated from the Hubble Deep Field and is thus the repository of most of the nuclear energy released by stars (Schlegel, Finkbeiner and Davis 1998; Hauser et al. 1998). The total mass in baryons in stars even allowing for a maximal shrouded population must however still be small. It is also interesting to compare the estimated total energy density with the corresponding global production of heavy elements. Taking the total bolometric intensity of starlight to be about 50 n W m-2 sr-1 (based on Schlegel et al.'s fitted value 32 ± 13 at 140 µm), the energy density is
where the redshift factor corrects for energy lost after the
mean epoch of emission. Each nucleon that is burned to helium
releases 25 MeV in heat,
rising to a total of about 30 MeV per nucleon converted from hydrogen
to heavy elements. On dividing u by 30 MeV we get the mean
nucleon number density in heavy elements produced in the
production of the background light,
nheavy ~ 4 x 10-10 (1 + z) cm-3.
Our central value for the baryon number density is
nbaryons = 1.1 x 10-7 cm-3; the
ratio is the mass fraction in heavy elements to make the
observed background,
If the bulk of the radiation were produced at z = 2 it would mean
Z is about 1 percent. Though not a precise constraint,
it is a significant check that the number
roughly agrees with the observed metallicity of baryonic material.
Black Holes. -
Baryons sequestered in black holes in the luminous parts of
normal galaxies are known to be subdominant to the baryons in
stars. It is quite unreasonable to imagine whole galaxies have
been lost to relativistic collapse. Gas clouds at the Jeans
length at decoupling may be susceptible to relativistic collapse
but only a tiny fraction of material has small enough
angular momentum to form black holes, and
even then it is hard to imagine an appreciable
fraction of the cloud mass could collapse before the remainder is
blown apart by radiation from the collapsing fraction.
Far before recombination even a tiny collapsing fraction yields
a significant mass fraction today, although it
requires either extremely large amplitude
perturbations in
Baryonic MACHOs. - Debris is a key issue for MACHOs interpreted
as star remnants. In known processes of formation of
white dwarfs and neutron stars, winds and explosions disperse
most of the original star mass in
diffuse debris. Thus a 2M
Plasma Around Field Galaxies. -
There is a significant baryon density in stars in normal
galaxies, and a still larger density in plasma around the
galaxies. The latter is the largest and most uncertain entry in
our baryon budget at low redshift in
Table 3. The
estimate in line (7') assumes the spheroid
star-to-gravitational mass
ratio is the same in clusters and the field. If we have missed a
significant mass in spheroids, as in LSB galaxies, and the
missing fraction is the same in clusters and the field, it does
not affect the estimate. If spheroid star production were more
efficient in clusters it would mean that the estimated
group mass is too small and hence line (7') is too
small. If plasma were ejected (more than
spheroid stars) from clusters during assembly, line (7')
would be an overestimate. But neither of these
effects could be large without upsetting the condordance
between equations (24), (25) and (27). Comparison of the two estimates,
line (7') and the sum of lines (7a) and (7b), shows a
factor of two difference, but it is easy to imagine that
this is because the X-ray observations still miss considerable warm
plasma and we have not yet adequately modeled the cooler low surface
density clouds detected by absorption lines at low
redshift.
Baryons in the Voids. -
There are galaxies in the low density regions, or voids, defined
by normal galaxies. Galaxies in low density regions tend to be
the later Hubble types, and so are more readily observable than
their counterparts in concentrations. Gas enrichment aside, no
known type of object prefers the voids. This includes dwarf and
irregular galaxies, low surface brightness galaxies, and the
plasma clouds detected from absorption lines. The reasonable
presumption is that plasma clusters the way all other observed
baryons do, meaning there is not much mass in plasma in the
voids. The possible exception is gas with high enough pressure
to resist gravitational draining of the voids, but if the
density of such void plasma were comparable to that
estimated in groups it would have appeared already as excessive
helium absorption at z
The lack of reasonable-looking alternatives leads us to conclude that
a fair accounting of the the baryons is possible because most are
in states that can be observed or reliably constrained by
more indirect arguments. We now argue that there is a reasonable
case for the net baryon density parameter
close to the central value of the sum in line 8 in
Table 3.
,
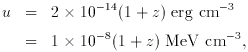
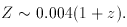
which tends to adversely affect the model for
light element production (e.g.,
Kurki-Suonio, Jedamzik, &
Mathews 1996),
or extreme fine tuning of the spectrum and amplitude of
small-scale adiabatic perturbations
(Carr 1994).
In these scenarios baryons may be sequestered in compact objects at
redshifts z 
1010 that are in effect nonbaryonic for the purpose of this paper.
star leaves
a 0.5M remnant
and 1.5M in
debris, and the ejected fraction is larger for larger stars. The lensing
observations are consistent with a density parameter
~ 0.25 in MACHOs,
which would be a very considerable entry in the budget, but we
would have to explain what happened to the debris.
The debris might be recycled and a large fraction ultimately
sequestered in many generations of MACHOs, but recycling
seems unlikely in the low density halos of galaxies. Debris still
present as diffuse matter, with density parameter 
0.014, would violate
constraints previously discussed on diffuse matter
in groups and most models would also generate
excessive metals. The most plausible form of baryons is
brown dwarfs, though
this would require a second peak in the global IMF.
Brown dwarf masses are below the estimated mass range of
the observed MACHOs, but this could be the result of an
unfortunate distribution of velocities of the MACHOs in the
direction of the LMC. Absent the discovery of observational
evidence for the brown dwarf picture, or the demonstration that
the formation of star remnants
need not disperse much debris in observable forms,
we suspect the MACHO contribution to the
baryon budget is subdominant to the mass in plasma around groups.
3.
