4. DID CLUSTERS FORM FROM GAUSSIAN FLUCTUATIONS?

Since clusters are held together by gravity, the final step in the creation of a cluster must be controlled by gravity. In gravitational instability pictures, it usually is assumed that clusters grew by gravity out of primeval mass fluctuations that approximated a homogeneous and isotropic random Gaussian process. This Gaussian assumption certainly is one of the first cases to try because it is simple, and it follows in the simplest inflation models where homogeneity is perturbed by quantum fluctuations of an almost free field, which would be a Gaussian process. But people have devised schemes for producing non-Gaussian mass fluctuations out of inflation (Ortolan, Lucchin and Matarrese 1988; Peebles 1989); and it is of course possible that structure is not to be understood within the inflation scenario. In particular, the cosmic string (Turok 1985) and explosion (Weinberg, Ostriker, and Dekel 1989) pictures produce distinctly non-Gaussian seeds. Thus it would be very helpful to know whether or not the large-scale structure of the universe is consistent with gravitational growth from Gaussian initial mass density fluctuations (Peebles 1983).

Let us consider the typical mass within the Abell radius in a rich cluster of galaxies. The answer to our question, whether this mass could have grown out of Gaussian initial fluctuations, depends on parameters that are not yet sufficiently well constrained, but still it is interesting to explore what would be needed. By the conventional estimates reviewed below, clusters could have grown out of Gaussian fluctuations if (1) the mass within the Abell radius were assembled at low redshifts, z_f ~ 0.5, (2) the universe were Einstein-de Sitter, and (3) the present large-scale fluctuations in mass are down from the fluctuations in galaxy counts by the factor favored by Kaiser (1988):

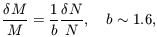
(8)

Each of these assumptions is under some challenge, which makes for an interesting situation.

The standard way to analyze the development of rare mass concentrations by gravitational instability is described and applied by Kaiser and Davis (1985) and Efstathiou and Rees (1988). One considers the mass distribution in the early universe, when density fluctuations were supposed to be small, and one estimates the ratio v of the mass fluctuation needed to produce a prominent object such as a cluster to the rms fluctuation in mass on the same scale. If v is larger than 5 or so, then under the Gaussian assumption these prominent objects ought to be vanishingly rare, while they of course could be common under other distributions.

The estimate of the ratio is

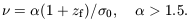
(10)

Here z_f is the redshift at which the mass observed within some fixed part of the cluster first became concentrated to a density large compared to the background. The observed mass defines a comoving volume in the early universe; ₀ is the rms fractional fluctuation in mass within this volume extrapolated to the present according to linear perturbation theory, (1 + z)^-1 in an Einstein-de Sitter universe. The bound on the constant is from the discussion of Peebles, Daly and Juszkiewicz (1989).

Now let us estimate the quantities in equation (10). The mean mass of an Abell cluster within the Abell radius is given by equation (4). The comoving radius of a sphere that contains this mass in an Einstein de Sitter universe is

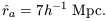
(11)

The present mean square fluctuation in galaxy counts within a sphere of this radius is

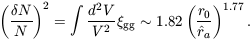
(12)

This uses the power law form for the galaxy two-point correlation function, _gg = (r₀ / r)^1.77, with r₀ = 5.4h^-1 Mpc. If we convert N / N to M / M using equation (9), with b = 1.6, we get ₀ ~ 0.7. A lower bound z_f > 0.5 for assembly of the mass seems safe, because at that redshift ~ 70 percent of the cluster members have the spectra characteristic of quiescent present day E and S0 galaxies (Dressler and Gunn 1988), suggesting they already were in place in a dense environment. This gives ~ 3.2, which is a reasonable number for rare peaks. However, if astronomical evidence forced z_f up to 1.5, say, or b to the value b ~ 2.5 favored by some, it would be a serious problem for the Gaussian picture and an interesting clue to cluster formation.

This research was supported in part by the National Science Foundation.