


A decade ago, at least five models for the origin of galaxies and their clustered spatial distribution were under active discussion (Peebles & Silk 1990). Five years later the community had settled on the adiabatic CDM model. That was in part because simple versions of the competing models were shown to fail, and in part because the CDM model was seen to be successful enough to be worthy of close analysis. But the universe is a complicated place: it would hardly be surprising to learn that several of the processes under discussion in 1990 prove to be significant dynamical actors, maybe along with things we haven't even thought of yet. That motivated my possibly overwrought lists of issues in lines 3a to 3e in the table.
I spent a lot of time devising alternatives to the CDM model. My feeling was that such a simple picture, that we hit on so early in the search for ideas on how structure formed, could easily fail, and it would be prudent to have backups. Each of my alternatives was ruled out by the inexorable advance of the measurements, mainly of the power spectrum of fluctuations in the temperature of the CBR. The details can be traced back through Hu & Peebles (2000). The experience makes me all the more deeply impressed by the dramatic success of the CDM model in relating observationally acceptable cosmological parameters to the measured temperature fluctuation spectrum (Hu et al 2000 and references therein).
This interpretation is not unique.
McGaugh (2000)
presents a useful though not yet
completely developed alternative, that assumes there is no
nonbaryonic dark matter
-  baryon =
baryon =
 m ~ 0.04 - and assumes a
modification to the gravitational inverse square law on
large scales - following
Milgrom (1983)
- drives structure
formation. But the broad success of the CDM model makes a strong
case that this is a good approximation to what happened as matter
and radiation decoupled at redshift z ~ 1000. An update of
Table 1 would considerably enlarge
entry 5.
m ~ 0.04 - and assumes a
modification to the gravitational inverse square law on
large scales - following
Milgrom (1983)
- drives structure
formation. But the broad success of the CDM model makes a strong
case that this is a good approximation to what happened as matter
and radiation decoupled at redshift z ~ 1000. An update of
Table 1 would considerably enlarge
entry 5.
If the CDM model really is the right interpretation of the CBR anisotropy it leaves considerable room for adjustment of the details. I turn now to two issues buried in the table that might motivate a critical examination of details.
The issue of what is in the voids defined by the concentrations of observed galaxies and gas clouds is discussed at length in Peebles (2001); here is a summary of the main points.
The familiar textbook, optically selected, galaxies are strongly clustered, leaving large regions - voids - where the number density of galaxies is well below the cosmic mean. Galaxies with low gas content and little evidence of ongoing star formation prefer dense regions; gas-rich galaxies prefer the lower ambient density near the edges of voids. This is the morphology-density correlation.
The CDM model predicts that the morphology-density correlation extends to the voids, where the morphological mix swings to favor dark galaxies. But the observations require this swing to be close to discontinuous. A substantial astronomical literature documents the tendency of galaxies of all known types - dwarfs, irregulars, star forming, low surface brightness, and purely gaseous - to avoid the same void regions. There are some galaxies in voids, but they are not all that unusual, apart from the tendency for greater gas content.
The natural interpretation of these phenomena is that gravity has
emptied the voids of most galaxies of all types, and with them
drained away most of the low pressure mass. This is is not
allowed in the Einstein-de Sitter model. If the mass
corresponding to
 m = 1 were
clustered with the galaxies
the gravitational accelerations would be expected to produce
peculiar velocities well in excess of what is observed. That is,
if
m = 1 were
clustered with the galaxies
the gravitational accelerations would be expected to produce
peculiar velocities well in excess of what is observed. That is,
if  m = 1 most of
the mass would have to be in the voids,
and the morphology-density correlation would have to include the
curious discontinuous swing to a mix dominated by dark galaxies in
voids. That is why I put so much weight on the dynamical evidence
for low
m = 1 most of
the mass would have to be in the voids,
and the morphology-density correlation would have to include the
curious discontinuous swing to a mix dominated by dark galaxies in
voids. That is why I put so much weight on the dynamical evidence
for low  m.
m.
At  m = 0.25 ±
0.10 (eq. [7]) the mass
fraction in voids can be as small as the galaxy fraction. That
would neatly remove the discontinuity. But gravity does not empty
the voids in numerical simulations of the low density CDM model.
In the simulations massive dark mass halos that seem to be
suitable homes for ordinary optically selected galaxies form in
concentrations. This is good. But spreading away from
these concentrations are dark mass halos that are too small for
ordinary galaxies, but seem to be capable of developing into
dwarfs or irregulars. This is contrary to the observations.
m = 0.25 ±
0.10 (eq. [7]) the mass
fraction in voids can be as small as the galaxy fraction. That
would neatly remove the discontinuity. But gravity does not empty
the voids in numerical simulations of the low density CDM model.
In the simulations massive dark mass halos that seem to be
suitable homes for ordinary optically selected galaxies form in
concentrations. This is good. But spreading away from
these concentrations are dark mass halos that are too small for
ordinary galaxies, but seem to be capable of developing into
dwarfs or irregulars. This is contrary to the observations.
The consensus in the theoretical community is that the predicted dark mass clumps in the voids need not be a problem, because we don't know how galaxies form, how to make the connection between dark mass halos in a simulation and galaxies in the real world. The point is valid, but we have some guidance, from what is observed. Here is an example.
The Local Group of galaxies contains two large spirals, our Milky Way and the somewhat more massive Andromeda Nebula. There many smaller galaxies, most tightly clustered around the two spirals. But some half dozen irregular galaxies, similar to the Magellanic clouds, are on the outskirts of the group. These irregulars have small velocities relative to the Local Group. Since they are not near either of the large galaxies they are not likely to have been spawned by tidal tails or other nonlinear process. Since they are at ambient densities close to the cosmic mean their first substantial star populations would have formed under conditions not very different from the voids at the same epoch. In short, these objects seem to prove by their existence that observable galaxies can form under conditions similar to the voids in CDM simulations. Why are such galaxies so rare in the voids?
4.2. The Epoch of Galaxy Formation
Numerical simulations of the CDM model indicate galaxies were assembled relatively recently, at redshift z ~ 1 (eg. Cen & Ostriker 2000). For definiteness in explaining what bothers me about this I adopt the density parameter in equation (7) and Hubble parameter Ho = 70 km s-1 Mpc-1.
The mass in the central luminous parts of a spiral galaxy is
dominated by stars. The outer parts are thought to be dominated
by nonbaryonic dark matter. The circular velocity vc of a
particle gravitationally bound in a circular orbit in the galaxy
varies only slowly with the radius of the orbit,
and there is not a pronounced change in vc at the transition
between the luminous inner part and the dark outer part. The
value of the mean mass density
 ( < r)
averaged within a
sphere of radius r centered on the galaxy relative to the
cosmic mean mass density,
( < r)
averaged within a
sphere of radius r centered on the galaxy relative to the
cosmic mean mass density,
 , is
, is
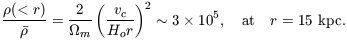
| (8) |
At this radius the mass of the typical spiral is thought to be dominated by nonbaryonic dark matter. Why is the dark mass density so large? Options are that
To avoid confusion let us pause to consider the distinction between interpretations of large density contrasts in the luminous baryonic central regions and in the dark halo of a galaxy. If the baryons and dark matter were well mixed at high redshift, the baryon-dominated central parts of the galaxies would have to have been the result of settling of the baryons relative to the dark matter. Gneddin, Norman, and Ostriker (2000) present a numerical simulation that demonstrates dissipative settling of the baryons to satisfactory stellar bulges. The result is attractive - and hardly surprising since gaseous baryons tend to dissipatively settle - but does not address the issue at hand: how did the dark matter halos that are thought to be made of dissipationless matter get to be so dense?
We have one guide from the great clusters of galaxies. The
cluster mass is thought to be dominated by nonbaryonic matter. A
typical line-of-sight velocity dispersion is
 = 750 km s-1. The
mean mass density averaged within
the Abell radius, rA = 2 Mpc, relative to the cosmic
mean, is
= 750 km s-1. The
mean mass density averaged within
the Abell radius, rA = 2 Mpc, relative to the cosmic
mean, is
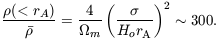
| (8) |
Clusters tend to be clumpy at the Abell radius, apparently still relaxing to statistical equilibrium after the last major mergers, but they are thought to be close to dynamic equilibrium, gravity balanced by streaming motions of the galaxies and mass. This argues against the first of the above ideas: here are dark matter concentrations that have relaxed to dynamical support at density contrast well below the dark halo of a galaxy (eq. [8]).
The second idea to consider is that a dense dark matter halo is
assembled at low redshift by the merging of a collection of dense
lower mass halos that formed earlier. This is what happens in
numerical simulations of the CDM model.
Sometimes cited as an example in Nature is the projected
merging of the two Local Group spirals, the Milky Way and the
Andromeda Nebula. They are 750 kpc apart, and moving together at
100 km s-1. If they moved to a direct hit they would merge
in another Hubble time. But that would require either wonderfully
close to radial motion or dynamical drag sufficient to eliminate
the relative orbital angular momentum. Orbit computations
indicate masses that would be contained in
 r-2
dark halos truncated at r ~ 200 kpc, which seems small for
dissipation of the orbital angular momentum. The computations
suggest the transverse relative velocity is comparable to the
radial component
(Peebles, Shaya
& Tully 2000).
That would say
the next perigalacticon will be at a separation ~ 300 kpc,
not favorable for merging. Thus I suspect the Local Group spirals
will remain distinct elements of the galaxy clustering hierarchy
well beyond one present Hubble time. If
the Local Group is gravitationally bound and remains isolated the
two spirals must eventually merge, but not on the
time scale of the late galaxy formation picture.
r-2
dark halos truncated at r ~ 200 kpc, which seems small for
dissipation of the orbital angular momentum. The computations
suggest the transverse relative velocity is comparable to the
radial component
(Peebles, Shaya
& Tully 2000).
That would say
the next perigalacticon will be at a separation ~ 300 kpc,
not favorable for merging. Thus I suspect the Local Group spirals
will remain distinct elements of the galaxy clustering hierarchy
well beyond one present Hubble time. If
the Local Group is gravitationally bound and remains isolated the
two spirals must eventually merge, but not on the
time scale of the late galaxy formation picture.
My doubts are reenforced by the failure to observe precursors of galaxies. Galaxy spheroids - elliptical galaxies and the bulges in spirals that look like ellipticals - are dominated by old stars. Thus it is thought that if present-day spheroids were assembled at z ~ 1 it would have been by the merging of star clusters. These star clusters might have been observable at redshift z > 1, as a strongly clustered population, but they are not.
That leaves the third idea, early galaxy assembly. I am not aware of any conflict with what is observed at z < 1. The observations of what happened at higher redshift are rich, growing, and under debate.