


To a second order approximation we can characterize the temperature structure of a gaseous nebula by two parameters: the average temperature, T0, and the root mean square temperature fluctuation, t, given by
and
respectively, where Ne and Ni are
the electron and the ion densities of the
observed emission line and V is the observed volume
(Peimbert 1967;
Osterbrock 1970).
To determine T0 and t2 we need two
different methods to derive Te: one
that weights preferentially the high temperature regions and one that
weights preferentially the low temperature regions. For example the
temperature derived from the ratio of the [O III]
and
respectively. It is also possible to use the intensity ratio of a
collisionally excited
line of an element p + 1 times ionized to a recombination line of
the same
element p times ionized, this ratio is independent of the element
abundance and depends only on the electron temperature. By combining this
ratio with a temperature determined from the ratio of two collisionally
excited lines like Te(4363/5007) it is also possible
to derive T0 and t2.
To determine abundance ratios, Te(4363/5007) has been
used very often under
the assumption that t2 = 0.00. In the presence of
temperature variations however,
the use of Te(4363/5007) yields O abundances that are
smaller than the real ones (e.g.
Peimbert 1967;
Peimbert & Costero
1969).
In general, abundance
ratios derived from the ratio of a collisionally excited line to a
recombination line are underestimated, while those derived from the ratio of
two collisionally excited lines with similar excitation energies or from the
ratio of two recombination lines, are almost independent of
t2. Nevertheless
for some applications like the determination of the primordial helium
abundance, which is based on the ratio of recombination lines, the errors
introduced by adopting a t2 = 0.00 value are very
small but non-negligible.
From observations it has been found that 0.01
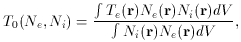
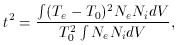

 4363, 5007
lines, Te(4363/5007), and the temperature derived from
the ratio of the
Balmer continuum to I(H
4363, 5007
lines, Te(4363/5007), and the temperature derived from
the ratio of the
Balmer continuum to I(H  ), Te(Bac /
H
), Te(Bac /
H  ), that are
given by
), that are
given by
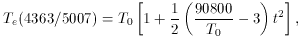
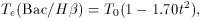
 t2
t2
 0.09, with
typical values around 0.04; while from photoionization models of
chemically and density homogeneous nebulae it has been found that
0.00
0.09, with
typical values around 0.04; while from photoionization models of
chemically and density homogeneous nebulae it has been found that
0.00  t2
t2
 0.02, with typical values around
0.005. An explanation
for the differences in the t2 values predicted by
photoionization models and those found by observations has to be sought.
0.02, with typical values around
0.005. An explanation
for the differences in the t2 values predicted by
photoionization models and those found by observations has to be sought.