


Recent reviews on abundances derived from extragalactic H II regions are those by Shields (1990) and Dinerstein (1990). Sets of photoionization models that can be used for the study of extragalactic H II regions have been presented by Stasinska (1990) and Gruenwald & Viegas (1992).
As for PN and galactic H II regions there is plenty of evidence for the presence of mechanical energy input in addition to photoionization in giant extragalactic H II regions.
Many giant H II regions show line profiles that indicate supersonic velocities (e.g. Meaburn 1984; Iye, Ulrich & Peimbert 1987; Castañeda, Vilchez & Copetti 1990a, b). Moreover probably all giant extragalactic H II regions present supersonic velocities since Chu and Kennicutt (1994) find that all the LMC H II regions observed by them -30- present supersonic velocity dispersions; the most spectacular structures in 30 Doradus are several fast expandind shells which according to them appear to be produced, at least partially, by SNR. These supersonic velocities should be produced by stellar activity inside H II regions.
There are plenty of arguments in favor of exploding supernovae inside H II regions and of winds produced by O stars and WR stars. Five out of eleven known supernovae of Type Ib exploded in H II regions (Wheeler, Harkness & Capellaro 1987). Five out of eight oxygen-rich supernova remnants are found inside H II regions (van den Bergh 1988). Peimbert, Sarmiento & Fierro (1991) estimate that half of the O stars will explode as SN inside H II regions. Rosa & Mathis (1987) have found an O/H rich region inside 30 Doradus that they attribute to mass loss from a massive star inside the nebula.
The difficulty of measuring
I( 4363) (or any other direct
temperature indicator) led
Pagel et al. (1979)
to propose an empirical
method based on the ratio of the nebular oxygen lines to
H
4363) (or any other direct
temperature indicator) led
Pagel et al. (1979)
to propose an empirical
method based on the ratio of the nebular oxygen lines to
H , R23
, R23
 ([O II]
([O II] 3727 +
[O III]
3727 +
[O III]
 4959, 5007) /
H
4959, 5007) /
H , to determine
Te and the O/H ratio. There are significant
differences between the calibration of Pagel's method to determine O/H
ratios for extragalactic H II regions based on models
(McCall, Rybski &
Shields 1985;
Dopita & Evans 1986;
McGaugh 1991)
and the calibrations based on observations
(Edmunds & Pagel
1984;
Torres-Peimbert et
al. 1989).
The differences are in the 0.2 dex to 0.4 dex range and could be
mainly due to the presence of temperature inhomogeneities over the observed
volume (Campbell
1988;
Torres-Peimbert et
al. 1989;
McGaugh 1991).
While the calibration based on models adjusts the observed
R23 values with
those derived from photoionization models (with
< t2 > ~
0.005), the calibration based on observations adjusts the observed
R23
values with the abundances derived from Te(4363/5007)
under the assumption that t2 = 0.00.
Peimbert et
al. (1991)
have found that by adding a
supernova remnant to an H II region ionized by 100 O stars the ([O
III]
, to determine
Te and the O/H ratio. There are significant
differences between the calibration of Pagel's method to determine O/H
ratios for extragalactic H II regions based on models
(McCall, Rybski &
Shields 1985;
Dopita & Evans 1986;
McGaugh 1991)
and the calibrations based on observations
(Edmunds & Pagel
1984;
Torres-Peimbert et
al. 1989).
The differences are in the 0.2 dex to 0.4 dex range and could be
mainly due to the presence of temperature inhomogeneities over the observed
volume (Campbell
1988;
Torres-Peimbert et
al. 1989;
McGaugh 1991).
While the calibration based on models adjusts the observed
R23 values with
those derived from photoionization models (with
< t2 > ~
0.005), the calibration based on observations adjusts the observed
R23
values with the abundances derived from Te(4363/5007)
under the assumption that t2 = 0.00.
Peimbert et
al. (1991)
have found that by adding a
supernova remnant to an H II region ionized by 100 O stars the ([O
III] 4363) /
H
4363) /
H ratio varies by a
large factor while the R23 ratio
is almost unaffected. From this result it follows that in the presence of
shock waves Pagel's method is an excellent tool to derive the O/H ratio
as long as it is calibrated with the R23 ratio predicted by
photoionization models and not with the observed
Te(4363/5007) value under
the assumption that t2 = 0.00.
ratio varies by a
large factor while the R23 ratio
is almost unaffected. From this result it follows that in the presence of
shock waves Pagel's method is an excellent tool to derive the O/H ratio
as long as it is calibrated with the R23 ratio predicted by
photoionization models and not with the observed
Te(4363/5007) value under
the assumption that t2 = 0.00.
Pagel et al. (1992), based on abundances derived from Te(4363/5007) under the assumption that t2 = 0.00, found that H II regions with WR features show a larger scatter in the N versus Y diagram than those without WR features, they suggested that the scatter could be due to Y and N selfenrichment. Esteban and Peimbert (1995) from modelling the chemical evolution of H II regions due to selfenrichment, based on the stellar evolution modls by Maeder (1992), find that the Y and N enrichment produce displacements in the N versus Y diagram that are parallel to the fit, obtained by Pagel et al., for the H II regions without WR features. Esteban & Peimbert suggest that the Y and N overabundances might be illusory and could be due to higher t2 values than for H II regions without WR features.
From a selected group of well observed H II regions, where those with WR
features were omitted, Pagel et al. (1992) found
 Y /
Y /
 O =
10.2 ± 3.5 by assuming that: a) t2 = 0.00,
b) no O
trapped in dust grains and c) no deviations from case B of the
hydrogen lines. Pagel et al. recomended a
O =
10.2 ± 3.5 by assuming that: a) t2 = 0.00,
b) no O
trapped in dust grains and c) no deviations from case B of the
hydrogen lines. Pagel et al. recomended a
 Y /
Y /
 O ~
6.7 by considering: a) an increase of 0.04 dex due to
t2
O ~
6.7 by considering: a) an increase of 0.04 dex due to
t2  0.00, b) 0.08 dex of O trapped in dust grains and c)
possible deviations of the H lines from case B for the metal richer H II
regions.
0.00, b) 0.08 dex of O trapped in dust grains and c)
possible deviations of the H lines from case B for the metal richer H II
regions.
Carigi et al. (1994)
from a sample of 10 well observed extragalactic H II
regions derived  Y /
Y /
 O = 7.1 ± 1.6 for
t2 = 0.00
without considering the amount of O in dust grains nor deviations from case
B. The main difference in the
O = 7.1 ± 1.6 for
t2 = 0.00
without considering the amount of O in dust grains nor deviations from case
B. The main difference in the
 Y /
Y /
 O values between Carigi
et al. and
Pagel et al. (1992)
is due to the use by Carigi et al. of
recent results for the two metal poorest objects in their sample:
IZw 18 and UGC 4483
(Skillman &
Kennicutt 1993;
Skillman et
al. 1994).
Carigi et al. derived
O values between Carigi
et al. and
Pagel et al. (1992)
is due to the use by Carigi et al. of
recent results for the two metal poorest objects in their sample:
IZw 18 and UGC 4483
(Skillman &
Kennicutt 1993;
Skillman et
al. 1994).
Carigi et al. derived  Y
/
Y
/  O = 4.5 ± 1.0 for
t2 =
0.035 and adopting an increase of 0.04 dex in O due to the fraction
trapped in dust grains.
O = 4.5 ± 1.0 for
t2 =
0.035 and adopting an increase of 0.04 dex in O due to the fraction
trapped in dust grains.
To explain the large  Y /
Y /
 O ratios derived from samples
of galaxies it has been proposed that a galactic outflow of O-rich material
is present
(Aparicio et al. 1988;
Lequeux 1989;
Pilyugin 1993;
Tosi 1994;
Peimbert et
al. 1994a).
This outflow is characterized by
O ratios derived from samples
of galaxies it has been proposed that a galactic outflow of O-rich material
is present
(Aparicio et al. 1988;
Lequeux 1989;
Pilyugin 1993;
Tosi 1994;
Peimbert et
al. 1994a).
This outflow is characterized by
 , the
fraction of the mass ejected by supernovae to the intergalactic medium
without mixing with the interstellar gas.
, the
fraction of the mass ejected by supernovae to the intergalactic medium
without mixing with the interstellar gas.
Carigi et al. (1994)
from chemical evolution models of irregular galaxies
are able to fit the  Y /
Y /
 O (t2 =
0.035), C / O and
(Z-C-O) / O observational restrictions for
O (t2 =
0.035), C / O and
(Z-C-O) / O observational restrictions for
 = 0.23; for larger
values of
= 0.23; for larger
values of  they
can not adjust the C / O and (Z-C-O) / O constraints
while for smaller values of
they
can not adjust the C / O and (Z-C-O) / O constraints
while for smaller values of
 they can not adjust the
they can not adjust the
 Y /
Y /
 O ratio. The C / O and
(Z-C-O) / O ratios are
almost independent of t2 while
O ratio. The C / O and
(Z-C-O) / O ratios are
almost independent of t2 while
 Y /
Y /
 O depends
strongly on t2. Larger values of t2
will permit to adjust all the observational constraints for a smaller value of
O depends
strongly on t2. Larger values of t2
will permit to adjust all the observational constraints for a smaller value of
 .
.
An additional argument in favor of large t2 values of
O-poor H II regions is provided by
González-Delgado et al. (1995)
who find a
considerable smaller Te from the Paschen continuum to
H ratio than Te(4363/5007).
ratio than Te(4363/5007).
The most spectacular result of the study of abundances derived from gaseous nebulae is the determination of the primordial or pregalactic helium abundance, Yp, that has cosmological implications (e.g. Peimbert & Torres-Peimbert 1974, 1976; Boegsgaard & Steigman 1985; Pagel et al. 1992; Pagel 1995 and references therein). Yp is derived from the intensity ratios of He to H recombination lines in O-poor extragalactic H II regions assuming that
where Y and O are the helium and oxygen mass fractions of each
H II region and 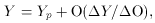
 Y /
Y /
 O - assumed to be constant - is
the ratio
of the Y and O enrichments of the interstellar medium after the galaxies
were formed. The H and He
recombination line intensities to a first approximation are inversely
proportional to Te, to a second approximation they
show small
differences in their Te dependence (e.g.
Hummer & Storey
1987;
Smits 1994).
The differences are such that for t2 = 0.04 the
Yp value
becomes about 0.003 smaller than for t2 =
0.00. Alternatively for those
objects for which collisional excitations from the 23S level are
considerable a t2
O - assumed to be constant - is
the ratio
of the Y and O enrichments of the interstellar medium after the galaxies
were formed. The H and He
recombination line intensities to a first approximation are inversely
proportional to Te, to a second approximation they
show small
differences in their Te dependence (e.g.
Hummer & Storey
1987;
Smits 1994).
The differences are such that for t2 = 0.04 the
Yp value
becomes about 0.003 smaller than for t2 =
0.00. Alternatively for those
objects for which collisional excitations from the 23S level are
considerable a t2
 0.00 will increase the derived
Y value (see
Figure 1). The densities of most
extragalactic H II regions are typically
around 100 cm-3, considerably
smaller than the critical density (see equation 3.7); consequently the
collisional effects are practically negligible for these objects,
therefore t2
0.00 will increase the derived
Y value (see
Figure 1). The densities of most
extragalactic H II regions are typically
around 100 cm-3, considerably
smaller than the critical density (see equation 3.7); consequently the
collisional effects are practically negligible for these objects,
therefore t2  0.00
will reduce the derived Yp value.
0.00
will reduce the derived Yp value.