

© CAMBRIDGE UNIVERSITY PRESS 1999
| |
1.6.2 Cosmic Inflation: Introduction
The basic idea of inflation is that before the universe entered the present adiabatically expanding Friedmann era, it underwent a period of de Sitter exponential expansion of the scale factor, termed inflation (Guth 1981). Actually, inflation is never precisely de Sitter, and any superluminal (faster-than-light) expansion is now called inflation. Inflation was originally invented to solve the problem of too many GUT monopoles, which, as mentioned in the previous section, would otherwise be disastrous for cosmology.
The de Sitter cosmology corresponds to the solution of
Friedmann's equation in an empty universe (i.e.,
with  = 0) with vanishing
curvature (k = 0) and positive cosmological constant
(
= 0) with vanishing
curvature (k = 0) and positive cosmological constant
( > 0). The solution is
a = a0 eHt,
with constant Hubble parameter H =
(
> 0). The solution is
a = a0 eHt,
with constant Hubble parameter H =
( /3)1/2.
There are analogous solutions for k = +1 and k = -1 with
a
/3)1/2.
There are analogous solutions for k = +1 and k = -1 with
a  cosh Ht and
a
cosh Ht and
a  sinh Ht
respectively. The scale factor expands exponentially because the
positive cosmological constant corresponds effectively to a
negative pressure. de Sitter space is discussed in textbooks
on general relativity (for example,
Rindler 1977,
Hawking & Ellis 1973)
mainly for its
geometrical interest. Until cosmological inflation was considered,
the chief significance of the de Sitter solution in cosmology was that it is a
limit to which all indefinitely expanding models with
sinh Ht
respectively. The scale factor expands exponentially because the
positive cosmological constant corresponds effectively to a
negative pressure. de Sitter space is discussed in textbooks
on general relativity (for example,
Rindler 1977,
Hawking & Ellis 1973)
mainly for its
geometrical interest. Until cosmological inflation was considered,
the chief significance of the de Sitter solution in cosmology was that it is a
limit to which all indefinitely expanding models with
 > 0
must tend, since as a ->
> 0
must tend, since as a ->
 , the cosmological
constant term ultimately dominates the right hand side of the
Friedmann equation.
, the cosmological
constant term ultimately dominates the right hand side of the
Friedmann equation.
As Guth (1981) emphasized, the de Sitter solution might also have been important in the very early universe because the vacuum energy that plays such an important role in spontaneously broken gauge theories also acts as an effective cosmological constant. A period of de Sitter inflation preceding ordinary radiation-dominated Friedmann expansion could explain several features of the observed universe that otherwise appear to require very special initial conditions: the horizon, flatness/age, monopole, and structure formation problems. (See Table 1.6.)

|
Let us illustrate how inflation can help with the horizon
problem. At recombination (p+ + e- -> H),
which occurs at a / a0
 10-3, the mass
encompassed
by the horizon was Mh
10-3, the mass
encompassed
by the horizon was Mh
 1018
M
1018
M , compared
to Mh,0
, compared
to Mh,0  1022 M
1022 M today. Equivalently,
the angular size today of the causally connected regions at recombination
is only
today. Equivalently,
the angular size today of the causally connected regions at recombination
is only 
 ~ 3°. Yet the fluctuation
in temperature of the cosmic background radiation from
different regions is very small:
~ 3°. Yet the fluctuation
in temperature of the cosmic background radiation from
different regions is very small:
 T/T ~
10-5. How could
regions far out of causal contact have come to temperatures
that are so precisely equal? This is the ``horizon
problem''. With inflation, it is no problem because the
entire observable universe initially lay inside a single
causally connected region that subsequently inflated to a
gigantic scale. Similarly, inflation exponentially dilutes
any preceeding density of monopoles or other unwanted
relics (a modern version of the ``dragons'' that decorated
the unexplored borders of old maps).
T/T ~
10-5. How could
regions far out of causal contact have come to temperatures
that are so precisely equal? This is the ``horizon
problem''. With inflation, it is no problem because the
entire observable universe initially lay inside a single
causally connected region that subsequently inflated to a
gigantic scale. Similarly, inflation exponentially dilutes
any preceeding density of monopoles or other unwanted
relics (a modern version of the ``dragons'' that decorated
the unexplored borders of old maps).
In the first inflationary models, the dynamics of the very early
universe was typically controlled by the self-energy of the
Higgs field associated with the breaking of a Grand Unified
Theory (GUT) into the standard 3-2-1 model: GUT ->
SU(3)color 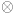 [SU(2)
[SU(2) 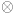 U(1)]electroweak.
This occurs when the cosmological temperature drops to the
unification scale TGUT ~ 1014 GeV at about
10-35 s after the Big Bang.
Guth (1981)
initially considered a scheme in
which inflation occurs while the universe is trapped in an
unstable state (with the GUT unbroken) on the wrong side of
a maximum in the Higgs potential. This turns out not to
work: the transition from a de Sitter to a Friedmann
universe never finishes
(Guth & Weinberg
1981).
The solution in the ``new inflation'' scheme
(Linde 1982;
Albrecht and
Steinhardt 1982)
is for inflation to occur after barrier penetration
(if any). It is necessary that the potential of the
scalar field controlling inflation (``inflaton'') be nearly
flat (i.e., decrease very slowly with increasing inflaton field)
for the inflationary period to last long enough. This nearly
flat part of the potential must then be followed by a
very steep minimum, in order that the energy contained in
the Higgs potential be rapidly shared with the other degrees
of freedom (``reheating''). A more general approach,
``chaotic'' inflation, has been worked out by Linde
(1983,
1990)
and others; this works for a wide range of inflationary
potentials, including simple power laws such as
U(1)]electroweak.
This occurs when the cosmological temperature drops to the
unification scale TGUT ~ 1014 GeV at about
10-35 s after the Big Bang.
Guth (1981)
initially considered a scheme in
which inflation occurs while the universe is trapped in an
unstable state (with the GUT unbroken) on the wrong side of
a maximum in the Higgs potential. This turns out not to
work: the transition from a de Sitter to a Friedmann
universe never finishes
(Guth & Weinberg
1981).
The solution in the ``new inflation'' scheme
(Linde 1982;
Albrecht and
Steinhardt 1982)
is for inflation to occur after barrier penetration
(if any). It is necessary that the potential of the
scalar field controlling inflation (``inflaton'') be nearly
flat (i.e., decrease very slowly with increasing inflaton field)
for the inflationary period to last long enough. This nearly
flat part of the potential must then be followed by a
very steep minimum, in order that the energy contained in
the Higgs potential be rapidly shared with the other degrees
of freedom (``reheating''). A more general approach,
``chaotic'' inflation, has been worked out by Linde
(1983,
1990)
and others; this works for a wide range of inflationary
potentials, including simple power laws such as 
 4. However, for the
amplitude of the fluctuations to
be small enough for consistency with observations, it is necessary
that the inflaton self-coupling be very small, for example
4. However, for the
amplitude of the fluctuations to
be small enough for consistency with observations, it is necessary
that the inflaton self-coupling be very small, for example  ~ 10-14 for the
~ 10-14 for the  4 model. This requirement prevents a
Higgs field from being the inflaton, since Higgs fields by definition
have gauge couplings to the gauge field (which are expected to be of
order unity), and these would generate self-couplings of similar
magnitude even if none were present. Both the Higgs and inflaton are
hypothetical fundamental (or possibly composite) scalar fields (see
Table 1.6).
4 model. This requirement prevents a
Higgs field from being the inflaton, since Higgs fields by definition
have gauge couplings to the gauge field (which are expected to be of
order unity), and these would generate self-couplings of similar
magnitude even if none were present. Both the Higgs and inflaton are
hypothetical fundamental (or possibly composite) scalar fields (see
Table 1.6).
It turns out to be necessary to inflate by a factor  e66 in order to solve the flatness problem, i.e., that
e66 in order to solve the flatness problem, i.e., that
 0 ~ 1. (With
H-1 ~ 10-34 s during the
de Sitter phase, this implies that the inflationary period
needs to last for only a relatively small time
0 ~ 1. (With
H-1 ~ 10-34 s during the
de Sitter phase, this implies that the inflationary period
needs to last for only a relatively small time 
 10-32 s.) The ``flatness problem'' is
essentially the question why the universe did not become curvature dominated
long ago. Neglecting the cosmological constant on the
assumption that it is unimportant after the inflationary
epoch, the Friedmann equation can be written
10-32 s.) The ``flatness problem'' is
essentially the question why the universe did not become curvature dominated
long ago. Neglecting the cosmological constant on the
assumption that it is unimportant after the inflationary
epoch, the Friedmann equation can be written
where the first term on the right hand side is the
contribution of the energy density in relativistic particles
and g (T) is the effective number of degrees of freedom.
The second term on the
right hand side is the curvature term. Since aT
Of course, this is only the minimum amount of inflation needed; the
actual inflation might have been much greater. Indeed it is frequently
argued that since the amount of inflation is a tremendously sensitive
function of e.g., the initial value of the inflaton field, it is
extremely likely that there was much more inflation than the minimum
necessary to account for the fact that 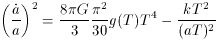
 constant for adiabatic expansion, it is clear that as the
temperature T drops, the curvature term becomes
increasingly important. The quantity K
constant for adiabatic expansion, it is clear that as the
temperature T drops, the curvature term becomes
increasingly important. The quantity K  k / (aT)2 is
a dimensionless measure of the curvature.
Today, |K| = |
k / (aT)2 is
a dimensionless measure of the curvature.
Today, |K| = |  - 1|
H02 / T02
- 1|
H02 / T02
 2 x 10-58. Unless
the curvature exactly vanishes, the most ``natural'' value
for K is perhaps K ~ 1.
Since inflation increases a by a tremendous factor
eH
2 x 10-58. Unless
the curvature exactly vanishes, the most ``natural'' value
for K is perhaps K ~ 1.
Since inflation increases a by a tremendous factor
eH at essentially
constant T (after reheating),
it increases aT by the same tremendous factor and thereby
decreases the curvature by that factor squared. Setting
e-2H
at essentially
constant T (after reheating),
it increases aT by the same tremendous factor and thereby
decreases the curvature by that factor squared. Setting
e-2H
 2 x 10-58
gives the needed
amount of inflation: H
2 x 10-58
gives the needed
amount of inflation: H
 66. This much
inflation turns out to be enough to take care of the other
cosmological problems mentioned above as well.
66. This much
inflation turns out to be enough to take care of the other
cosmological problems mentioned above as well.
 0 is of order unity. It then follows that the
curvature constant is probably vanishingly small after inflation, which
implies (in the absence of a cosmological constant today) that
0 is of order unity. It then follows that the
curvature constant is probably vanishingly small after inflation, which
implies (in the absence of a cosmological constant today) that  0 = 1 to a very high
degree of accuracy.
A way of evading this that has recently been worked out is discussed
below.
0 = 1 to a very high
degree of accuracy.
A way of evading this that has recently been worked out is discussed
below.