


To find a PG, one must have some idea of what one is searching for. Here we discuss a few of the (more or less) model independent properties of PGs, and the relation of these properties to search strategies.
2.1
Surface Density
Suppose that PGs are found only at redshift zPG, and have a
lifetime in a ``recognizable PG phase'' of  tPG. Further
suppose that the present-day descendants of PGs possess number density
n0 at the present epoch. The number of PGs visible in
a solid angle
tPG. Further
suppose that the present-day descendants of PGs possess number density
n0 at the present epoch. The number of PGs visible in
a solid angle 
 can then (neglecting mergers) be
written as
can then (neglecting mergers) be
written as
where dA is angular diameter distance. Now, the
luminosity density of the Universe (in B) is ~ 2.4 x
108 hLB
for
Meier (1976)
first demonstrated that the flux
F
in the wavelength range 1000Å-3600Å, for a
Salpeter (1955)
initial mass function (IMF)
(2). There is some dependence of
Eq. (3) on burst
age and IMF, but in all cases the variation is less than a factor of
three in
Some spectral energy distributions (SEDs) of stellar populations with
a constant star formation rate of 1 M
A typical PG will contain many individual star formation regions, and
so the overall star formation rate should be smoothly varying on time
scales longer than the age of the most massive stars and shorter than
the collapse time tcoll (~ 109 yr). Thus it
seems reasonable
to characterize a PG by some mean star formation rate, from which a
rough estimate of < F
One effect that might cause a real PG to deviate from the idealization
of Eq. (3) is dust absorption. One magnitude of absorption in the V
band is roughly equivalent to 4.4 mag of absorption at 1000Å (e.g.,
Seaton 1979).
(This is illustrated in Fig. 2)
The absorbed UV radiation is re-emitted thermally at wavelengths of
order 100µm, as in starburst galaxies. The relevance of
this to PG searches will be discussed further in
Section 6.
The flux predicted by Eq. (3) is from stellar
photospheres alone. Real PG spectra will also show strong emission lines due
to excitation of gas by UV photons from hot stars. A simple
calculation based on Kennicutt's (1983) calibration of H
The principal source of energy from PGs is the release of nuclear
binding energy from fusion reactions in stars. Energy release from
AGN's may be comparable, but the connection of the AGN phenomenon
with galaxy formation is unclear, and the lifetimes of individual AGN
sources are uncertain. Other sources of energy (such as gravitational
binding energy release from galaxy formation or star formation, or
energy release from supernovae) are smaller by 1-2 orders of magnitude
(Djorgovski and Weir 1990, Djorgovski 1992).
A crude estimate of the luminosity of a PG can be obtained as follows.
A PG will convert a fraction Z
where MPG is here the baryonic mass of the PG. The
apparent brightness of such a source at z = 5
(h50 = 1,
A somewhat more accurate approach to calculating the continuum
brightness of PGs
is simply to use the relation between star formation rate and
F
Thus it appears that PGs may be visible in continuum light in the
optical-near infared bands, but of course
only provided that the wavelength of observation lies redward of
the Lyman discontinuity - i.e.,
It is of interest to consider the total surface brightness of PGs on
the sky. One could approximate this quantity by simply multiplying the
characteristic surface density of PGs (Eq. (1)) by their brightness
(from Eq. (4)). A more exact, more elegant, and physically more
revealing approach is to consider the production of metals (Lilly and
Cowie 1987, Cowie 1988). The basic point of this approach
is that energy production and
metal production are closely linked processes. From arguments similar
to those leading to Eq. (4), it is straightforward to show that a
production rate of metals of 1 M
where
The limit from eqn. (5) (µAB
The visual appearance of a PG has been subject to a great deal of
speculation. If the observable PG phase were the end product of the
monolitic collapse of a massive cloud of gas (as proposed by, for
example, Eggen,
Lynden-Bell, and Sandage 1962; see also Larson 1974),
then the bulk of its star formation might occur in a small region
kiloparsecs in size (where 1 kpc
On the other hand, some models of galaxy formation (e.g., BW87) predict
that PGs will be lumpy in structure and extended in size, primarily due
to the fact that in these models galaxy formation is a hierachical
process. The BW87 models predict PGs that are ~ 5-10" in
size, with individual knots that may be bright enough to be visible.
An extreme model would be the case in which there are a very large
number of star formation sites spread throughout a large, more or less
uncollapsed halo; the individual star forming subunits would not be visible
as discrete entities. Such an object would have very low surface
brightness (~ 30 mag arcsec-2), a size of perhaps
10-20", and would be extremely difficult to detect using
conventional techniques. (Nevertheless, it seems plausible that
at least some of the gas in such an extended configuration would find
its way into a nuclear starburst by dissipation.)
The redshift of galaxy formation, zGF, is of great
importance in deciding on a PG search strategy, since
zGF determines both
how bright a PG will be, and in what wavelength range a search should
optimally be conducted.
In this paper we will concentrate, as do many other authors (BW87,
White 1989),
on the formation of spheroidal systems. There is in
fact very good evidence that the formation of disks is more quiescent
than that of spheroids (e.g., Gunn 1982), and that disks were never much
brighter than they are today
(3). For example, Larson (1992)
summarizes
evidence that the mean SFR in the disks of nearby spirals (including
the Milky Way - e.g., discussion in Majewski 1993)
was never much more than twice the present value.
Recent estimates of the gas consumption timescales in disks yield mean
values ~ 7 Gyr (cf. Kennicutt 1983,
Sandage 1986,
Donas et
al. 1987; see also discussion in
Larson
1992). This is not too different
from the ages of disks, suggesting that, with a modest amount of
infall, the mean SFR need not have been too different from the present
value. This is all supported by the observations of Cowie, Songaila,
and Hu (1993), who present direct evidence of the gradual growth of
disks. From their observations it appears that disks may have grown by
a factor of ~ 2-4X in mass since z
There is also some evidence that the bulk of disk formation followed
well after spheroid formation for the Milky Way (e.g., review by Norris
1989). The most direct information on this point comes from the work
of Winget et
al. (1987) on the low luminosity cutoff in the white dwarf
luminosity function. From this work it appears that the age of the disk
is most likely
If the age of the Universe T0 > 14 Gyr and the age of
the disk is
Thus in what follows we will consider the epoch of galaxy formation to
be the time at which the spheroid forms. In this picture the buildup of
the disk might be thought of as a manifestation of galaxy evolution
rather than galaxy formation.
2.5.1 Some Simple Model Independent Arguments
There are several arguments for the redshift of galaxy formation that
are more or less independent of an assumed model for galaxy formation
(Peebles
1989; see also
Peebles 1993,
Section 25). Most provide upper limits
to the redshift of galaxy formation.
(1)
(e.g., Peebles
1980, Section 11). Thus at least some
galaxy formation must occur at quite large redshift in a low
(2) Overlap argument. Consider the precursors of galaxies as spheres.
At what redshift were these spheres just touching?
The separation of galaxies at this epoch was ~ 2 fc R, where
R is the radius of the halo of the Milky Way (~ 100 kpc), and
fc is the amount by which the proto-halo collapsed
before forming stars. (Dissipationless collapse provides a lower limit
on fc of 2.)
The present-day separation of L* galaxies is ~
n0-1/3, where
n0 is the present-day number density ofL* galaxies
(e.g., Section 2.1). Then
Clearly this is a reasonable upper limit to the redshift of
galaxy formation for L* galaxies.
(3) Density argument. An interesting constraint on
zGF for L* galaxies
is obtained by finding the redshift at which the mean density of
galaxies at the present epoch was just equal to the density of the Universe.
This is an upper limit on zGF for any
reasonable model of galaxy formation.
For a galaxy with total (i.e., dark plus baryonic)
mass 1012 M
from which we find
One could repeat the above considering baryonic matter only (M
(4) Collapse argument. Perhaps the most physically insightful of
arguments is derived from consideration of an expanding perturbation in
the early Universe.
It is straightforward to show that the collapse time (time for a perturbation
to expand with the Hubble flow, turn around, and collapse completely) is just
where Rmax is the radius of the perturbation at
turnaround (Rmax = fc
R
2.5.2 The Empirical Evidence
There is a strong body of empirical evidence that can be marshalled to
place constraints on zGF, and also on the nature of PGs.
(1) Redshift surveys. A number of redshift surveys at faint
magnitudes have been conducted over the past few years (e.g.,
Broadhurst, Ellis
and Shanks 1988;
Colless et
al. 1990,
1993;
Lilly 1993;
Tresse et
al. 1993). From these surveys, it is clear that widespread
galaxy formation activity is not occurring at z
That is not to say that some galaxy formation activity is not still
underway at the present epoch
(4). Individual low luminosity objects
undergoing an intense burst of star formation are seen nearby (e.g., H II
region galaxies - Terlevich 1988; blue compact dwarf galaxies - Thuan
1987). A debate continues as to whether these objects really are
undergoing their first burst of star formation, or whether there is an
underlying old population
(Thuan 1987;
Keel 1988;
Meurer, Mackie,
and Carignan 1994). Nevertheless, these objects comprise
a tiny fraction of all
nearby galaxies. It should also be noted that a significant fraction of
the metals in present-day galaxies appears to be produced by the faint blue
galaxy population at z < 1
(Cowie, Lilly,
Gardner, and McLean 1988), although
if these galaxies are low mass then their metal-enriched gas may be expelled.
But these objects are not, we believe, the long sought after
primeval galaxies; they represent, rather, relatively recent galaxy
evolution, possibly driven by mergers, of a low mass galaxy population
(e.g., Cowie,
Songaila, and Hu 1993).
(2) Cluster ellipticals. The small scatter in the colors of
cluster ellipticals in the Virgo and Coma clusters provides an
interesting constraint on the redshift of formation of ellipticals
(Bower, Lucey,
and Ellis 1992). If galaxy ages differ typically by an
amount of order their collapse time (i.e.,
(3) Milky Way globular clusters. The ages of globular clusters
in the Milky Way are now know to span a range of at least ~ 3 Gyr (cf.
VandenBerg,
Bolte, and Stetson 1990;
Sarajedini and
Demarque 1990).
A reasonable assumption is that globular cluster formation starts no
earlier than the epoch of maximum expansion of a perturbation
(tcoll / 2). For a collapse time of
The above argument is probably one of the more powerful empirical arguments
available on the epoch of galaxy formation, but it is not without problems.
It is unclear whether the formation of globular clusters coincides with
the formation of the halo/spheroid of the Milky Way, or, for that matter,
whether there is a similar spread in ages found in field halo stars that
would indicate a prolonged period of halo formation, independently of the
globular clusters.
(4) Damped Ly
If the damped Ly
(5) High redshift radio galaxies. The SEDs of luminous, high
redshift radio galaxies in principle offer an opportunity to determine
their redshift of formation. There seem to be two distinct
interpretations of the spectra of these radio galaxies (e.g.,
McCarthy
1993a); (i) they form at high redshift (zGF > 5),
but are
viewed at an epoch at which they are undergoing a small (in fractional
mass) burst of star formation (Lilly 1988); or (ii) they are
viewed shortly after their formation epoch
(Chambers and
Charlot 1990),
a view that leads to estimates of zGF more like 3-4. The
remarkable tightness of the K-band Hubble diagram
(Lilly 1989;
McCarthy
1993a, Section 6.5) seems to
argue for a relatively high zGF 5; but this assumes no
evolution in the masses of radio galaxies
with redshift (see also discussion in Eales et
al. 1993).
The most recent work on radio galaxies at high redshift indicates that
the high z radio galaxies may well be a ``mixed bag'' in terms of
origin. Very blue objects such as 0902+34 (Eisenhardt and
Dickinson 1992) and the bluest objects in the survey of
McCarthy 1993b) may
have formation redshifts as small as 3-4 (see also Eales and Rawlings
1993). On the other hand, the reddest objects observed by McCarthy
seem to require much larger formation redshifts. Nevertheless, these
objects could have spurious colors due to non-stellar light or
emission lines (Eales and Rawlings 1993). In addition, it appears
that the colors of these objects are not, in any
case, well-matched by models (e.g., Fig. 2 of McCarthy 1993b).
Given all of the above, plus the fact that radio galaxies are not
typical of the general population of galaxies, we view constraints on
galaxy formation redshift from these objects with suspicion.
(6) Cosmic microwave background radiation. At a given epoch, small
amplitude perturbations will take longer to grow into galaxies than
large amplitude perturbations. Hence it follows that perturbations at
z
(7) Quasars. There are several ways of using quasars as indicators
of the redshift of galaxy formation. The first is to note that the peak
in the space density of quasars lies around z = 2-3 (e.g.,
Crampton, Cowley,
and Hartwick 1987;
Schmidt,
Schneider, and Gunn 1991).
If quasars are fueled by mergers (Carlberg 1990), and if mergers
play an important role in galaxy formation (e.g.,
White and Frenk
1991),
then it seems reasonable to suppose that the peak of the
``galaxy-building'' epoch lies at or around z = 2. Note however that
this argument associates no particular importance to quasars in
relation to galaxy formation, other than as an indicator of the merger
rate (but see Djorgovski 1994).
2.5.3 Redshift of Galaxy Formation - A Summary
As noted above, the two most interesting pieces of empirical evidence
constraining the epoch of galaxy formation are (i) the age spread
of Milky Way globular clusters, and (ii) a direct estimate of gas
depletion (presumably due to star formation) from
observations of damped Ly
This moderately self-consistent picture is, however, disturbed by two
recent papers by Turner (1991a,
b), who
convincingly demonstrates that
the properties of quasars at high redshift demand at least some
galaxy formation activity at z
A related argument is that the presence of heavy element absorption
lines in the spectra of quasars implies that significant star formation
and chemical enrichment has occurred along random lines of sight in the
Universe significantly earlier than z
It seems most reasonable to conclude, then, that, even if the bulk of
galaxy formation activity takes place at z
As was discussed in Section 1, the
principal focus of this
review is on the detection of a widespread, high surface density population
of PG's that should exist in all directions in the sky. Nevertheless,
it is of interest to briefly mention some objects or classes of objects
which have been proposed as candidate PG's.
We have already mentioned (Section 2.5) the
possibility that QSO's or
powerful radio galaxies might have been PG's at some stage of their evolution.
There is also evidence that the somewhat weaker (~ 0.1 Jy)
radio source 53W002 may be close to its
initial star burst. This object was discovered in the Leiden-Berkeley
Deep Survey, and was found to be narrow-line galaxy with redshift z =
2.39 (Windhorst
et al. 1991). It appears to have started forming stars
only ~ 0.5 Gyr earlier than its epoch of observation, placing the
redshift of galaxy formation zGF
A class of superluminous, IR-bright galaxies has been identified that
may be related to the PG phenomenon. The best-known member of this
class is the z = 2.286 IRAS galaxy F10214+4724, which, with a
bolometric luminosity of > 1014 L
Damped Ly
3 A clear counterexample, however, is the Large Margellanic Cloud.
Back.
4 Nevertheless, galaxy formation
activity at z = 0
must be nearly finished, because most (> 90%) of the baryonic material
locally appears not to be in the form of gas. Back.
5 Songaila et al. (1994) have recently determined the
deuterium
to hydrogen ratio in a z = 3.3 cloud towards a QSO. Their result implies
a primordial 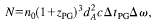
 Mpc-3 (Felten 1985), and the characteristic luminosity of galaxies
is L*B
Mpc-3 (Felten 1985), and the characteristic luminosity of galaxies
is L*B  1.6 x 1010 h-2
LB
1.6 x 1010 h-2
LB (very
similar to the luminosity of the Milky Way), where h =
H0/100 and H0 is in
km s-1 Mpc-1. Hence a reasonable estimate for the local
number density of L* galaxies is n0
(very
similar to the luminosity of the Milky Way), where h =
H0/100 and H0 is in
km s-1 Mpc-1. Hence a reasonable estimate for the local
number density of L* galaxies is n0  0.015 h3
Mpc-3. The surface density of such galaxies can therefore be
written as
0.015 h3
Mpc-3. The surface density of such galaxies can therefore be
written as
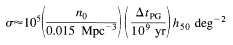
 0 = 1 and a
redshift of galaxy formation zPG = 5. (Here
h50 is the Hubble constant expressed in units of 50 km
s-1
Mpc-1. The choice of zPG and
0 = 1 and a
redshift of galaxy formation zPG = 5. (Here
h50 is the Hubble constant expressed in units of 50 km
s-1
Mpc-1. The choice of zPG and  tPG in this formula
will be justified below.) The numbers are even larger in an open
Universe. Thus the progenitors of galaxies like the Milky Way should be
very numerous, regardless of the exact choice of parameters in Eq. (2).
tPG in this formula
will be justified below.) The numbers are even larger in an open
Universe. Thus the progenitors of galaxies like the Milky Way should be
very numerous, regardless of the exact choice of parameters in Eq. (2).
2.2
Spectrum
 of an object with
constant star formation rate was roughly
flat between the Lyman and Balmer breaks, with F
of an object with
constant star formation rate was roughly
flat between the Lyman and Balmer breaks, with F proportional to the star formation
rate in this spectral region. This result is usually expressed as (e.g.,
Meier 1976,
Cowie 1988,
White 1989)
proportional to the star formation
rate in this spectral region. This result is usually expressed as (e.g.,
Meier 1976,
Cowie 1988,
White 1989)
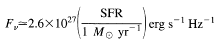

 .
.
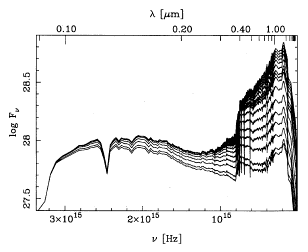 Figure 1. Spectral
energy distributions for stellar systems with a
constant star formation rate of 1 M
Figure 1. Spectral
energy distributions for stellar systems with a
constant star formation rate of 1 M yr-1 (from the models of
Bruzual and
Charlot 1993). The ages of these systems range from
4 x 107 yr (bottom) to 1010 yr (top). The vertical
axis is in units of erg s-1 Hz-1. The prominent
absorption feature near 1216Å is Ly
yr-1 (from the models of
Bruzual and
Charlot 1993). The ages of these systems range from
4 x 107 yr (bottom) to 1010 yr (top). The vertical
axis is in units of erg s-1 Hz-1. The prominent
absorption feature near 1216Å is Ly . Note the relatively flat energy distribution from
1000Å to 3600Å; also note that the flux level over this wavelength
range does not depend strongly on age. The total flux in the wavelength
range 1000Å-3600Å varies between 75% (4 x 107 yr) and 40%
(1010) of the total light beyond the Lyman discontinuity.
. Note the relatively flat energy distribution from
1000Å to 3600Å; also note that the flux level over this wavelength
range does not depend strongly on age. The total flux in the wavelength
range 1000Å-3600Å varies between 75% (4 x 107 yr) and 40%
(1010) of the total light beyond the Lyman discontinuity.
 yr-1 are shown in
Fig. 1 (from the models of
Bruzual and Charlot
1993). The main contributors to the light at
yr-1 are shown in
Fig. 1 (from the models of
Bruzual and Charlot
1993). The main contributors to the light at  < 3600Å are upper main
sequence stars; at longer wavelengths there is also a contribution from
supergiants, asymptotic giant branch, and finally giant stars as age
progresses. However, the contribution of these populations never
completely dominates the total energy output (at
least for galaxy ages less than ~ 1010 yr), provided that the
star formation rate remains roughly constant. Ignoring light below the
Lyman discontinuity, the fraction of the total luminosity in the
wavelength range 912Å-3600Å varies from 75% at an age of
4 x 107 yr, to 60% at 109 yr, to 40% at
1010 yr. (This ignores dust - see below.)
< 3600Å are upper main
sequence stars; at longer wavelengths there is also a contribution from
supergiants, asymptotic giant branch, and finally giant stars as age
progresses. However, the contribution of these populations never
completely dominates the total energy output (at
least for galaxy ages less than ~ 1010 yr), provided that the
star formation rate remains roughly constant. Ignoring light below the
Lyman discontinuity, the fraction of the total luminosity in the
wavelength range 912Å-3600Å varies from 75% at an age of
4 x 107 yr, to 60% at 109 yr, to 40% at
1010 yr. (This ignores dust - see below.)
 > follows. In the Baron and
White (1987, hereafter BW87) galaxy formation scenario (see below), the
star formation rate is in fact predicted to be roughly constant over
nearly one collapse time.
> follows. In the Baron and
White (1987, hereafter BW87) galaxy formation scenario (see below), the
star formation rate is in fact predicted to be roughly constant over
nearly one collapse time.
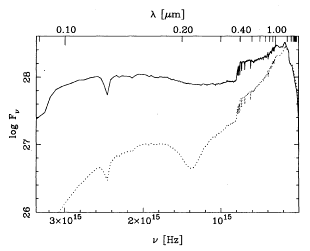 Figure 2. The effect of
1 mag of V-band absorption on the
spectral energy distribution of a 109 yr old stellar population with
constant star formation rate. The solid line shows the SED with
no absorption, whereas the dotted line includes absorption. The
absorption law is the Galactic extinction model of
Fitzpatrick (1986)
for
Figure 2. The effect of
1 mag of V-band absorption on the
spectral energy distribution of a 109 yr old stellar population with
constant star formation rate. The solid line shows the SED with
no absorption, whereas the dotted line includes absorption. The
absorption law is the Galactic extinction model of
Fitzpatrick (1986)
for  < 3600Å, with
modifications to match the absorption
measurements of Nandy et al. (1975) at longer wavelengths (see also
Seaton
1979). The basic unabsorbed model is from Bruzual and Charlot
(1993).
< 3600Å, with
modifications to match the absorption
measurements of Nandy et al. (1975) at longer wavelengths (see also
Seaton
1979). The basic unabsorbed model is from Bruzual and Charlot
(1993).
 strength vs. star formation rate, coupled with an H
strength vs. star formation rate, coupled with an H to H
to H intensity ratio from Case B recombination theory, and with
F
intensity ratio from Case B recombination theory, and with
F from
Eq. (3), yields a Ly
from
Eq. (3), yields a Ly equivalent
width of ~ 200Å (e.g.,
Djorgovski 1992). This implies that roughly 3-6% of the bolometric
luminosity from a PG should be emitted in Ly
equivalent
width of ~ 200Å (e.g.,
Djorgovski 1992). This implies that roughly 3-6% of the bolometric
luminosity from a PG should be emitted in Ly . More detailed
calculations by Charlot and Fall (1993) yield rest frame equivalent
widths in
the range 100-200Å (depending on the power law exponent of the
initial mass function), for a constant star formation rate; these
results are in quite good agreement with the simple empirical argument
above. The intensity of other lines, such as [O II] 3727Å, H
. More detailed
calculations by Charlot and Fall (1993) yield rest frame equivalent
widths in
the range 100-200Å (depending on the power law exponent of the
initial mass function), for a constant star formation rate; these
results are in quite good agreement with the simple empirical argument
above. The intensity of other lines, such as [O II] 3727Å, H 4861Å, [O III] 5007Å, and H
4861Å, [O III] 5007Å, and H 6563Å, is discussed in
Thompson,
Djorgovski, and Beckwith (1994); these lines are generally
weaker than H
6563Å, is discussed in
Thompson,
Djorgovski, and Beckwith (1994); these lines are generally
weaker than H , which itself is
about 8-11 x weaker than
Ly
, which itself is
about 8-11 x weaker than
Ly (Ferland and
Osterbrock 1985) in the absence of dust.
(Ferland and
Osterbrock 1985) in the absence of dust.
2.3
Luminosity
 -
-  X of its
hydrogen into metals; based on the metallicities of old disk stars,
|
X of its
hydrogen into metals; based on the metallicities of old disk stars,
| X|
X|  0.01. Approximately 1% of this
mass is converted into photons by release of binding energy in nuclear
reactions. The net bolometric luminosity of such a source is then
0.01. Approximately 1% of this
mass is converted into photons by release of binding energy in nuclear
reactions. The net bolometric luminosity of such a source is then
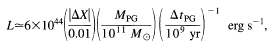
 0 = 1)
is about 2.8 x 10-15 erg cm-2 s-1, or,
in the AB magnitude system, mAB
0 = 1)
is about 2.8 x 10-15 erg cm-2 s-1, or,
in the AB magnitude system, mAB  24.5.
24.5.
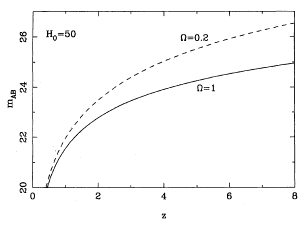 Figure 3. The AB
magnitude of objects with a constant star formation rate
of 100 M
Figure 3. The AB
magnitude of objects with a constant star formation rate
of 100 M yr-1, as a function of redshift. (In this
magnitude system mAB = 0 corresponds to
f
yr-1, as a function of redshift. (In this
magnitude system mAB = 0 corresponds to
f = 3.63 x
10-20
erg cm-2 s-1 Hz-1; see Oke [1974].) A
Hubble constant of 50 km s-1 Mpc-1 is assumed for
this diagram; the dashed line is
for
= 3.63 x
10-20
erg cm-2 s-1 Hz-1; see Oke [1974].) A
Hubble constant of 50 km s-1 Mpc-1 is assumed for
this diagram; the dashed line is
for  0 = 0.2, whereas
the solid line corresponds to
0 = 0.2, whereas
the solid line corresponds to  0 = 1.
This diagram is based on Eq. (4), and hence assumes that the wavelength
of observation corresponds to a restframe wavelength between the Lyman
and Balmer discontinuitues.
0 = 1.
This diagram is based on Eq. (4), and hence assumes that the wavelength
of observation corresponds to a restframe wavelength between the Lyman
and Balmer discontinuitues.
 in Eq. (3). The
result of such a calculation is shown in Fig. 3
for two cosmologies and a
star formation rate of 100 M
in Eq. (3). The
result of such a calculation is shown in Fig. 3
for two cosmologies and a
star formation rate of 100 M yr-1 [implicit in Eq. (4) above]. It
can be seen that the results of this calculation are in reasonable agreement
with the simple arguments above.
yr-1 [implicit in Eq. (4) above]. It
can be seen that the results of this calculation are in reasonable agreement
with the simple arguments above.

 (1 +
z) 912Å. For example, for observations in the I
band, PGs may be visible provided
that z
(1 +
z) 912Å. For example, for observations in the I
band, PGs may be visible provided
that z  8
(although the limiting magnitude of typical I band
surveys probably precludes observation beyond z
8
(although the limiting magnitude of typical I band
surveys probably precludes observation beyond z  4). The
situation is similar for ground-based observations in the 1-2.4
µm window: the sky brightness in the K band limits
observations to K < 23 or mAB < 25) (e.g.,
Gardner, Cowie,
and Wainscoat 1993),
so some PGs may be present in K band continuum surveys.
4). The
situation is similar for ground-based observations in the 1-2.4
µm window: the sky brightness in the K band limits
observations to K < 23 or mAB < 25) (e.g.,
Gardner, Cowie,
and Wainscoat 1993),
so some PGs may be present in K band continuum surveys.
 y-1 leads to a flux
F
y-1 leads to a flux
F = 2 x
1029 erg s-1 Hz-1, with very little
dependence on the choice of initial mass function. [Assuming a mean
metal yield ~ 1% then leads to Eq. (1), with, however, some IMF
sensitivity.] From this can be derived a surface
brightness due to metal formation of
= 2 x
1029 erg s-1 Hz-1, with very little
dependence on the choice of initial mass function. [Assuming a mean
metal yield ~ 1% then leads to Eq. (1), with, however, some IMF
sensitivity.] From this can be derived a surface
brightness due to metal formation of
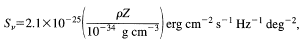
 Z is the
present day density of metals in the Universe.
With the indicated choice of
Z is the
present day density of metals in the Universe.
With the indicated choice of  Z (corresponding roughly to 1/3
solar metallicity - e.g., Cowie 1988), this works out to a surface
brightness µAB
Z (corresponding roughly to 1/3
solar metallicity - e.g., Cowie 1988), this works out to a surface
brightness µAB  31 mag arcsec-2. Note that this is not in
conflict with actual measurements of the background light; for example,
Dube, Wickes, and
Wilkinson (1979) derive an upper limit to the V
band background nearly 100X brighter. [Other upper limits to
background fluxes can be found in Fig. 2 of Cowie (1988) and Fig.
3 of De Jager,
Stecker, and Salamon (1994).]
31 mag arcsec-2. Note that this is not in
conflict with actual measurements of the background light; for example,
Dube, Wickes, and
Wilkinson (1979) derive an upper limit to the V
band background nearly 100X brighter. [Other upper limits to
background fluxes can be found in Fig. 2 of Cowie (1988) and Fig.
3 of De Jager,
Stecker, and Salamon (1994).]
 31 mag arcsec-2) can
be compared
with with background levels from known sources. From the number counts
of Lilly, Cowie,
and Gardner (1991), it can be seen that the surface
brightness in galaxies (for a 1 mag bin) is µAB
31 mag arcsec-2) can
be compared
with with background levels from known sources. From the number counts
of Lilly, Cowie,
and Gardner (1991), it can be seen that the surface
brightness in galaxies (for a 1 mag bin) is µAB
 30.9
mag arcsec-2 (at BAB = 25) and 30.0 mag
arcsec-2 (at IAB = 24). (These levels do
not depend strongly on magnitude because the logarithmic slope of
galaxy counts is fairly close to 0.4.) It is therefore possible
(although not proven) that a small fraction (< 10%) of galaxies
in faint galaxy surveys could be PG's.
30.9
mag arcsec-2 (at BAB = 25) and 30.0 mag
arcsec-2 (at IAB = 24). (These levels do
not depend strongly on magnitude because the logarithmic slope of
galaxy counts is fairly close to 0.4.) It is therefore possible
(although not proven) that a small fraction (< 10%) of galaxies
in faint galaxy surveys could be PG's.
2.4
Size and Morphology
 0".2-0".4,
depending on z and cosmology, although not with great sensitivity);
such an object would be close to being unresolved with a ground-based
telescope. An extreme example of such a model, in which most
star formation occurs in a very small region, is model A of Lin and Murray
(1992).
0".2-0".4,
depending on z and cosmology, although not with great sensitivity);
such an object would be close to being unresolved with a ground-based
telescope. An extreme example of such a model, in which most
star formation occurs in a very small region, is model A of Lin and Murray
(1992).
2.5
Redshift of Galaxy Formation
 1.
1.
 10 Gyr, which
is significantly younger than the
13-17 Gyr ages associated with (most) globular clusters (cf. Bergbusch and
VandenBerg 1992; Lee, Demarque, and Zinn 1990).
10 Gyr, which
is significantly younger than the
13-17 Gyr ages associated with (most) globular clusters (cf. Bergbusch and
VandenBerg 1992; Lee, Demarque, and Zinn 1990).
 10 Gyr, then this suggests
that the bulk of disk formation began
in earnest at z
10 Gyr, then this suggests
that the bulk of disk formation began
in earnest at z  1. Now, if most disk formation took place in a
short burst of activity at z
1. Now, if most disk formation took place in a
short burst of activity at z  1, then the objects involved should
stand out in existing faint object redshift surveys (e.g., Lilly 1993,
Colless et
al. 1990,
1993), since
they would have mAB
1, then the objects involved should
stand out in existing faint object redshift surveys (e.g., Lilly 1993,
Colless et
al. 1990,
1993), since
they would have mAB
 22-23. The
fact that they do not appear in these surveys strongly suggests that
these disks formed in a quiescent fashion over a much longer interval
of time.
22-23. The
fact that they do not appear in these surveys strongly suggests that
these disks formed in a quiescent fashion over a much longer interval
of time.
 argument. For a
Universe with
argument. For a
Universe with  0 < 1,
growth of
structure begins to freeze out at a redshift marking the transition
between Einstein-de Sitter expansion and linear expansion - i.e. at
0 < 1,
growth of
structure begins to freeze out at a redshift marking the transition
between Einstein-de Sitter expansion and linear expansion - i.e. at
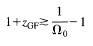
 Universe, although infall continues
right up to the present epoch in such a cosmological model.
Universe, although infall continues
right up to the present epoch in such a cosmological model.
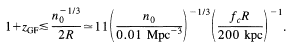
 , with total radius 100 kpc, the mean density
is ~ 2 x 1026 g cm-3, or a factor of
f3c smaller
before any collapse that took place. The matter density of the Universe
is
, with total radius 100 kpc, the mean density
is ~ 2 x 1026 g cm-3, or a factor of
f3c smaller
before any collapse that took place. The matter density of the Universe
is
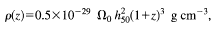
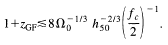
 1011 M
1011 M within R
within R  10 kpc for the Milky Way).
From nucleosynthesis constraints (Walker et al. 1991)
10 kpc for the Milky Way).
From nucleosynthesis constraints (Walker et al. 1991)  b < 0.1, and
fc
b < 0.1, and
fc
 10
by noting that the initial radius of the perturbation must have been
10
by noting that the initial radius of the perturbation must have been
 100 kpc. The result is
very similar: zGF
100 kpc. The result is
very similar: zGF  10.
10.
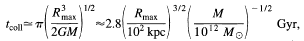
 200 kpc for the
Milky Way). To convert to a redshift requires a
choice of cosmology that gives a reasonable T0: for
example, if T0 = 13 Gyr, then zcoll
lies between 1.8 (h50 = 1,
200 kpc for the
Milky Way). To convert to a redshift requires a
choice of cosmology that gives a reasonable T0: for
example, if T0 = 13 Gyr, then zcoll
lies between 1.8 (h50 = 1,
 0 = 1) and 3.5
(h50 = 1.5,
0 = 1) and 3.5
(h50 = 1.5,  0 = 0) for galaxies like the Milky Way.
0 = 0) for galaxies like the Milky Way.
 1; otherwise PGs, given their
brightness at z
1; otherwise PGs, given their
brightness at z  1
(e.g., Fig. 3) and their surface density [Eq.
(2)], would appear prominently in current redshift surveys. Put another
way, the Universe at z
1
(e.g., Fig. 3) and their surface density [Eq.
(2)], would appear prominently in current redshift surveys. Put another
way, the Universe at z  1 is not too dissimilar to the Universe at the present
epoch (Peebles
1989).
1 is not too dissimilar to the Universe at the present
epoch (Peebles
1989).
 TGF
TGF  TGF, where TGF
corresponds to zGF), then zGF
TGF, where TGF
corresponds to zGF), then zGF  2
for luminous ellipticals. This lower limit on zGF could be
larger if any of the scatter in colors originated in intermediate
redshift starbursts.
2
for luminous ellipticals. This lower limit on zGF could be
larger if any of the scatter in colors originated in intermediate
redshift starbursts.
 109 yr, the
midpoint of the PG phase will then lie
109 yr, the
midpoint of the PG phase will then lie  2 Gyr after the big
bang, so that zGF
2 Gyr after the big
bang, so that zGF  2.5-4 (0.2
2.5-4 (0.2 
 0
0  1, 13
1, 13  T0
T0
 15 Gyr). In this picture the end
of the formation phase would be 3.5 Gyr after the big bang, or at
redshifts 1.5-2.2.
15 Gyr). In this picture the end
of the formation phase would be 3.5 Gyr after the big bang, or at
redshifts 1.5-2.2.
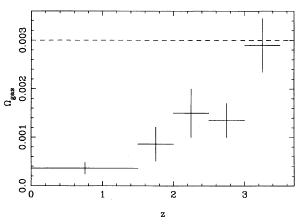 Figure 4. The fraction
of the critical density in damped Ly
Figure 4. The fraction
of the critical density in damped Ly absorbers,
absorbers,  gas, as a
function of redshift (from
Lanzetta 1993,
Lanzetta et
al. 1994). The dashed line indicates the present-day
density of luminous material (stars) in galaxies. It can be
seen that most galaxy formation has taken place since z = 3.5.
This diagram is for H0 = 100 km s-1
Mpc-1 and
gas, as a
function of redshift (from
Lanzetta 1993,
Lanzetta et
al. 1994). The dashed line indicates the present-day
density of luminous material (stars) in galaxies. It can be
seen that most galaxy formation has taken place since z = 3.5.
This diagram is for H0 = 100 km s-1
Mpc-1 and  0 = 1; both the data points and dashed line scale
as h-1.
0 = 1; both the data points and dashed line scale
as h-1.
 absorbers. Lanzetta and collaborators
(Lanzetta
1993;
Lanzetta, Wolfe,
and Turnshek 1994) have studied the amount
of gas in damped Ly
absorbers. Lanzetta and collaborators
(Lanzetta
1993;
Lanzetta, Wolfe,
and Turnshek 1994) have studied the amount
of gas in damped Ly absorbers
over a range of redshifts. Figure 4
plots their results for
absorbers
over a range of redshifts. Figure 4
plots their results for  gas, the density in
damped Ly
gas, the density in
damped Ly absorbers divided by
the critical density, as a function of
redshift; the present-day density of luminous material in galaxies and
disks is shown for comparison. It can be seen that
absorbers divided by
the critical density, as a function of
redshift; the present-day density of luminous material in galaxies and
disks is shown for comparison. It can be seen that  gas is
very similar to the value of
gas is
very similar to the value of  computed for stars in galaxies at the
present epoch. This result suggests that at least some damped Ly
computed for stars in galaxies at the
present epoch. This result suggests that at least some damped Ly systems originate in proto-spheroids; this is supported both by the
short time scale of gas consumption in Fig. 4
(
systems originate in proto-spheroids; this is supported both by the
short time scale of gas consumption in Fig. 4
( 1 Gyr), and also by
the low mean metallicity of these clouds (see
Lanzetta 1993
and Lanzetta et
al. 1994 for further details).
1 Gyr), and also by
the low mean metallicity of these clouds (see
Lanzetta 1993
and Lanzetta et
al. 1994 for further details).
 absorbers
really are the precursors of all modern-day
galaxies (5),
as is suggested by Fig. 4, then it follows that
much of the stellar mass in galaxies formed between z = 3.5 and 1.5,
and that perhaps half of these stars formed between z = 2-3.
absorbers
really are the precursors of all modern-day
galaxies (5),
as is suggested by Fig. 4, then it follows that
much of the stellar mass in galaxies formed between z = 3.5 and 1.5,
and that perhaps half of these stars formed between z = 2-3.
 1000, and hence
fluctuations in the cosmic microwave
background (CMB), must be larger if zGF is
increased. In order not
to violate the observed amplitude of CMB fluctuations,
zGF < 3-4 for a CDM model (Kashlinsky 1993,
Nusser and Silk
1993).
1000, and hence
fluctuations in the cosmic microwave
background (CMB), must be larger if zGF is
increased. In order not
to violate the observed amplitude of CMB fluctuations,
zGF < 3-4 for a CDM model (Kashlinsky 1993,
Nusser and Silk
1993).
 absorbers towards QSOs. These two
approaches yield characteristic epochs for the first burst of star
formation for most galaxies around z
absorbers towards QSOs. These two
approaches yield characteristic epochs for the first burst of star
formation for most galaxies around z  2-3. Somewhat
remarkably, this is in reasonable agreement with the predictions of the model
independent ``collapse argument'' above (for a collapse factor of
2), and with the existence of various ``primeval galaxy candidates''
discussed below. Furthermore, virtually all theories
of galaxy formation in a CDM-dominated Universe predict galaxy
formation at relatively low redshift (e.g., BW87,
Carlberg 1988).
2-3. Somewhat
remarkably, this is in reasonable agreement with the predictions of the model
independent ``collapse argument'' above (for a collapse factor of
2), and with the existence of various ``primeval galaxy candidates''
discussed below. Furthermore, virtually all theories
of galaxy formation in a CDM-dominated Universe predict galaxy
formation at relatively low redshift (e.g., BW87,
Carlberg 1988).
 5. For example, the very
existence of quasars at z = 5 implies structure formation and
collapse at much higher redshift. The fueling of QSO's at high
redshift requires the existence of high overdensity perturbations in
the accretion flow; otherwise the rate at which fuel can be supplied is
too low. The high abundance of heavy elements in quasars at z
5. For example, the very
existence of quasars at z = 5 implies structure formation and
collapse at much higher redshift. The fueling of QSO's at high
redshift requires the existence of high overdensity perturbations in
the accretion flow; otherwise the rate at which fuel can be supplied is
too low. The high abundance of heavy elements in quasars at z
 4
requires at least one (and possibly 2 for nitrogen) generations of
stars to preceed the quasar, and hence a redshift of galaxy formation
certainly greater than 5 (see also Hamann and Ferland
1993).
4
requires at least one (and possibly 2 for nitrogen) generations of
stars to preceed the quasar, and hence a redshift of galaxy formation
certainly greater than 5 (see also Hamann and Ferland
1993).
 4. Finally, Hu
and Ridgway (1994) have reported on the discovery of two extremely red
[(I - K) > 6] galaxies. The simplest explanation of the SEDs of these
objects is that they are ellipticals with an age
4. Finally, Hu
and Ridgway (1994) have reported on the discovery of two extremely red
[(I - K) > 6] galaxies. The simplest explanation of the SEDs of these
objects is that they are ellipticals with an age  3 Gyr at a
redshift z
3 Gyr at a
redshift z  2.4. This
requires (conservatively) a formation redshift > 6.
2.4. This
requires (conservatively) a formation redshift > 6.
 3.5, there must still
have been some galaxy formation activity at higher redshifts. In
fact this is not at all unreasonable, since the spectrum of
perturbations in the early Universe encompasses a wide range
of amplitudes and mass scales.
3.5, there must still
have been some galaxy formation activity at higher redshifts. In
fact this is not at all unreasonable, since the spectrum of
perturbations in the early Universe encompasses a wide range
of amplitudes and mass scales.
2.6
Primeval Galaxy Candidates
 2.7-4.2, depending on
cosmology (Windhorst, Mathis, and Keel 1992).
2.7-4.2, depending on
cosmology (Windhorst, Mathis, and Keel 1992).
 , is one of the most
powerful known sources in the Universe
(Rowan-Robinson
et al. 1991).
Two other objects, though not as extreme, are now known to resemble
F10214+4724:
P09104+4109 at z = 0.44
(Kleinmann and
Keel 1987), and
F15307+3252 at z = 0.93
(Cutri et
al. 1994). The z = 3.8
radio source
4C41.17 (Chambers, Miley, and van Breugel 1990) is somewhat
similar to
the extent that it is extremely luminous (L > 1013
L
, is one of the most
powerful known sources in the Universe
(Rowan-Robinson
et al. 1991).
Two other objects, though not as extreme, are now known to resemble
F10214+4724:
P09104+4109 at z = 0.44
(Kleinmann and
Keel 1987), and
F15307+3252 at z = 0.93
(Cutri et
al. 1994). The z = 3.8
radio source
4C41.17 (Chambers, Miley, and van Breugel 1990) is somewhat
similar to
the extent that it is extremely luminous (L > 1013
L ),
appears to be undergoing an intense burst of star formation, and contains
an enormous quantity of dust
(Dunlop et
al. 1994) - comparable to that
observed in F10214+4724. All of these sources can be interpreted as
being powered either by starbursts
(Brown and Vanden
Bout 1991;
Solomon, Downes,
and Radford 1992;
Rowan-Robinson et
al. 1993), or by AGNs
(Hines and Wills
1993;
Elston et
al. 1994). Regardless of the dominant
source of luminosity, it seems plausible
to suppose that these objects are massive elliptical galaxies in a very
early stage of evolution
(Kormendy and
Saunders 1992); the observations
of Elston et
al. (1994) do not rule out substantial star formation, and
are not in conflict with this interpretation. However, it is clear
that not all PG's could be like these objects; otherwise a huge
sub-mm background would result.
),
appears to be undergoing an intense burst of star formation, and contains
an enormous quantity of dust
(Dunlop et
al. 1994) - comparable to that
observed in F10214+4724. All of these sources can be interpreted as
being powered either by starbursts
(Brown and Vanden
Bout 1991;
Solomon, Downes,
and Radford 1992;
Rowan-Robinson et
al. 1993), or by AGNs
(Hines and Wills
1993;
Elston et
al. 1994). Regardless of the dominant
source of luminosity, it seems plausible
to suppose that these objects are massive elliptical galaxies in a very
early stage of evolution
(Kormendy and
Saunders 1992); the observations
of Elston et
al. (1994) do not rule out substantial star formation, and
are not in conflict with this interpretation. However, it is clear
that not all PG's could be like these objects; otherwise a huge
sub-mm background would result.
 absorbers may also be
related to PG's, as discussed in
the previous section. However, direct
evidence of star formation in these
objects is lacking, with the exception of ~ 3 absorbers that
possess emission lines (Elston et al. 1991, Wolfe et
al. 1992,
Møller and
Warren 1993). However, several Ly
absorbers may also be
related to PG's, as discussed in
the previous section. However, direct
evidence of star formation in these
objects is lacking, with the exception of ~ 3 absorbers that
possess emission lines (Elston et al. 1991, Wolfe et
al. 1992,
Møller and
Warren 1993). However, several Ly sources have been discovered
that are clustered around damped Ly
sources have been discovered
that are clustered around damped Ly absorbers (e.g.,
Lowenthal et
al. 1991;
Macchetto et
al. 1993;
Møller and
Warren 1993; see also
Wolfe 1993). The Macchetto et al. object is a
radio-quiet galaxy at z = 3.428 with strong Ly
absorbers (e.g.,
Lowenthal et
al. 1991;
Macchetto et
al. 1993;
Møller and
Warren 1993; see also
Wolfe 1993). The Macchetto et al. object is a
radio-quiet galaxy at z = 3.428 with strong Ly (rest frame
equivalent width
(rest frame
equivalent width  160Å), and an inferred star formation rate of
18 M
160Å), and an inferred star formation rate of
18 M yr-1. Both this object and the Lowenthal et al.
object, which it resembles, are candidates for PG's.
yr-1. Both this object and the Lowenthal et al.
object, which it resembles, are candidates for PG's.
2 The models of Bruzual and Charlot (1993) give about
2-3 times more flux than predicted by Eq. (3), most likely because
the upper main sequence models that they used included mild convective
overshooting, which lengthens main sequence lifetimes (S. Charlot,
private communication). Back.
 b h2 = 0.005, where
b h2 = 0.005, where  b is
b is  in
baryons; if this result is confirmed, then the damped Ly
in
baryons; if this result is confirmed, then the damped Ly absorbers must be the precursors of galaxies, because
absorbers must be the precursors of galaxies, because  b (damped
Ly
b (damped
Ly at z = 3.5)
at z = 3.5) 
 b (galaxies at z = 0)
b (galaxies at z = 0) 
 b
(primordial).
Back.
b
(primordial).
Back.