

It is 15 years since quasars were discovered, but there has been disappointingly slow progress towards achieving a consensus about what they are. There is now, however, wider agreement that quasars are not qualitatively different from other forms of activity in galactic nuclei, and this has deflated the more bizarre ideas that were aired in the early days. Radio and optical astronomers have accumulated a larger (and more systematic) body of data, from which we can infer details of the structure and radiation mechanism. Things become more conjectural as we attempt to extend the chain of inference back towards the central "power-house". But this, of course, is the most interesting and fundamental aspect of the quasar phenomenon.
Most interpretations of quasars invoke a mass of (say)
106-109
M in
a region
in
a region  1 pc in
size. The three well-known categories of model are
1 pc in
size. The three well-known categories of model are
 : dense star clusters
[1 -
6]
: dense star clusters
[1 -
6]
 : massive stars,
"spinars", or "magnetoids"
[1,
7]
: massive stars,
"spinars", or "magnetoids"
[1,
7]
 : accretion
onto massive black holes
[8 -
13].
: accretion
onto massive black holes
[8 -
13].
One can assess the maximum likely efficiency of the three types of
model. In case  , this is
essentially given by the maximum realizable
energy of a supernova-style explosion, or by the maximum amount of
binding energy that can be released via stellar collisions before the
star cluster "dissolves" into a single massive gas cloud. For
, this is
essentially given by the maximum realizable
energy of a supernova-style explosion, or by the maximum amount of
binding energy that can be released via stellar collisions before the
star cluster "dissolves" into a single massive gas cloud. For
 , the
limit is set by the onset of dynamical instability: rotation can
stabilize against the post-Newtonian instability, but a system that
becomes too flattened is vulnerable to bar-mode instabilities. One
cannot give firm estimates of the efficiencies attainable by models
, the
limit is set by the onset of dynamical instability: rotation can
stabilize against the post-Newtonian instability, but a system that
becomes too flattened is vulnerable to bar-mode instabilities. One
cannot give firm estimates of the efficiencies attainable by models
 and
and  , but there
would, I think, be general agreement that they cannot
be as high as the
, but there
would, I think, be general agreement that they cannot
be as high as the  10 percent
conversion of rest mass into
electromagnetic radiation that can be achieved via accretion into a
black hole.
10 percent
conversion of rest mass into
electromagnetic radiation that can be achieved via accretion into a
black hole.
A prerequisite for any model is the accumulation of a large mass
concentration, probably in the potential well as the center of a large
galaxy. Once this entity has reached the stage when its power output
(derived primarily from gravitational binding energy) becomes
conspicuous, one cannot envisage any evolutionary end-point other than
complete collapse of at least part of the material involved: in other
words, even if an accumulation of gas does not collapse directly to a
black hole, the progression
 (->
(->
 ) ->
) ->
 , or
, or
 ->
->
 , seems
inexorable. Given that any of the options lead to a black hole, and
that, once formed, a black hole is a potentially more efficient power
source than any conceivable progenitor, it seems plausible to
attribute quasars the most powerful known cosmic phenomena - to black
hole accretion processes: and then, as a secondary issue, to consider
precisely how they form, and whether precursor stages resembling
, seems
inexorable. Given that any of the options lead to a black hole, and
that, once formed, a black hole is a potentially more efficient power
source than any conceivable progenitor, it seems plausible to
attribute quasars the most powerful known cosmic phenomena - to black
hole accretion processes: and then, as a secondary issue, to consider
precisely how they form, and whether precursor stages resembling
 or
or
 can yield an
explanation of some less spectacular type of activity
in galactic nuclei.
can yield an
explanation of some less spectacular type of activity
in galactic nuclei.
Several new lines of evidence (some discussed by other contributors
to this conference) have tilted the balance of evidence further
towards models involving a single coherent and compact object (i.e.,
 or
or  above). For
instance: (1) the VLBI data seem inconsistent with a
simple "Christmas tree" model. (2) The compact radio components are
(in, e.g. 3C 111 and
Cygnus A) aligned along the same axis as the
extended double structure, indicating that the central "engine" has
maintained a preferred axis for millions of years. (3) There is
evidence from line ratios (and from possible variations) that the
broad emission lines come from regions of higher density and smaller
dimensions than envisaged in most previous models; the central
continuum source must be localized in a region of equally small
dimensions. (4) The variability cannot be readily analyzed into
successive standard supernova-type outbursts.
above). For
instance: (1) the VLBI data seem inconsistent with a
simple "Christmas tree" model. (2) The compact radio components are
(in, e.g. 3C 111 and
Cygnus A) aligned along the same axis as the
extended double structure, indicating that the central "engine" has
maintained a preferred axis for millions of years. (3) There is
evidence from line ratios (and from possible variations) that the
broad emission lines come from regions of higher density and smaller
dimensions than envisaged in most previous models; the central
continuum source must be localized in a region of equally small
dimensions. (4) The variability cannot be readily analyzed into
successive standard supernova-type outbursts.
In this paper, I shall focus on some aspects of the class of models
( ) in which the
power supply results from accretion onto a massive
black hole, omitting those aspects of the topic that are discussed
elsewhere in these proceedings. The required mass Mh
is typically in the
range 107-109
M
) in which the
power supply results from accretion onto a massive
black hole, omitting those aspects of the topic that are discussed
elsewhere in these proceedings. The required mass Mh
is typically in the
range 107-109
M , and the
minimum relevant length scale is then the Schwarzschild radius
, and the
minimum relevant length scale is then the Schwarzschild radius
If the efficience of energy conversion is
It is useful to define
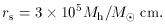
 , then the inflow rate
needed to provide a luminosity L is
, then the inflow rate
needed to provide a luminosity L is
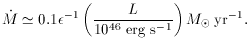
 crit as the value of
crit as the value of
 corresponding to a
luminosity Ledd
corresponding to a
luminosity Ledd  1.3 x 1038
(M/M
1.3 x 1038
(M/M ) erg
s-1.
) erg
s-1.