


11.1. Bar Formation
The bar instability was discovered in early N-body simulations of
rotating stellar disks
(Miller &
Prendergast 1968;
Hockney & Hohl 1969).
Because of these results, Kalnajs
(1971,
1972)
studied the
stability of disks with respect to bar modes through a linear analysis,
and made predictions about the eigenvalues and growth rates of the
normal modes for a given density and velocity distribution. These have
been verified by simulations in the linear regime (e.g.
Sellwood and
Athanassoula 1986).
Bars can be considered as long-lived modes, made by the superposition
of leading and trailing waves, i.e. forming a standing wave. As such,
the bar mode can grow through swing amplification, as outlined by
Toomre (1981)
for spiral density waves. The amplification of waves relies
on the corotation region (CR), which separates the galaxy into two
regions where the waves have opposite signs of energy and angular
momentum (negative inside and positive outside CR). At CR a wave will
be partially reflected and transmitted; the transmitted wave will carry
energy of opposite sign as the incident wave, so that the reflected
wave must have an increased amplitude to ensure conservation. The
corotation amplifier, coupled with a feedback cycle that reflects the
waves back to CR, can explain the growth of modes. Several feedback
cycles were proposed, such as the WASER
(Mark 1974b)
based on
long-trailing waves, while the swing involves the feedback of short
leading waves. In the WKB theory, waves are, however, evanescent around
CR, and tunnel through a forbidden zone
(Lin & Shu 1964);
the
exponential decrease of wave amplitude in this region kills the
amplifier, and the gain of the feedback cycles proposed is of the order
of unity. Actual amplitude gain over a cycle relies on another kind of
amplification, a positive feedback first identified by
Goldreich &
Lynden-Bell (1965)
and
Julian & Toomre (1966),
and detailed by
Toomre (1981),
with the help of numerical simulations.
The amplification is due to a conspiracy between differential rotation,
epicyclic oscillation, and self-gravity. Trailing density waves
propagate radially towards the center, while leading waves propagate
outwards. The leading wave packet becomes more and more open while
traveling, due to differential shear, until it turns into a trailing
wave. During this swing from leading to trailing, particles running on
their epicyclic motion closely follow the wave, and strongly interact
with it. Self-gravity contributes to gather particles, and amplify
their density contrast. The wave energy is amplified at the expense of
the rotational energy.
The trailing waves traveling inwards can be reflected in the center,
while the leading waves give rise to trailing reflected waves, and
transmitted waves at corotation. The reflection in the center occurs
only if a wave can travel there without being damped at the inner
Lindblad resonance. The problem of a possible Landau damping of waves
at the inner resonance has long suggested that bars can only develop
without this resonance. The pattern speed should then be high enough to
prevent the resonance. This appears to be verified in N-body
simulations in the linear regime, at the beginning of bar formation.
But it does not seem to be the rule in the non-linear regime in N-body
simulations, nor in the observations, when some hint can be gained of
the bar pattern speed.
Another point of view to better understand the N-body problem is in
terms of stellar orbits, and families of periodic orbits as will be
described in the next section. Periodic orbits are closed orbits in
the frame rotating with the bar. The stable ones trap regular orbits
around them. They are thus the skeleton of the orbital structure of the
disk. Periodic orbits are the fixed points that depend essentially on
the symmetry of the potential, and not on the detailed mass
distribution. In the potential of a rotating bar, the main family of
orbits is elongated along the bar, supporting it, and we can understand
under which conditions a self-gravitating system will become barred. When
the mass concentration towards the center is strong enough, the
elongated orbits will be replaced by periodic orbits perpendicular to
the bar, and we can predict the dissolution of the bar. This approach
can help to determine the pattern speed of realistic self-consistent
bars. Such an approach has been developed by Contopoulos and
collaborators (e.g.
Contopoulos &
Papayannopoulos 1980).
The consideration of near-resonant orbits aligned with the bar led
Lynden-Bell (1979)
to propose that bar instability could come from a
kind of Jeans instability, trapping all elongated orbits and aligning
their major axes. He studied the conditions under which an elongated
closed orbit in the bar rotating frame will be forced to align with the
bar, and therefore reinforce it, because of gravitational torques. He
concluded that for this to occur, the precession rate of elongated
orbits ( -
-  / 2) must increase with
specific angular
momentum, a condition that is fulfilled only in the central parts of
galaxies where the velocity curve is rising. The pattern speed of the
bar in this scenario must be lower than the peak of the
/ 2) must increase with
specific angular
momentum, a condition that is fulfilled only in the central parts of
galaxies where the velocity curve is rising. The pattern speed of the
bar in this scenario must be lower than the peak of the
 -
-  / 2 axisymmetric curve, which
is not the case at the
beginning of the bar instability in N-body simulations.
/ 2 axisymmetric curve, which
is not the case at the
beginning of the bar instability in N-body simulations.
The development of the instability has now been followed through a wide
series of N-body simulations (e.g.
Sellwood 1981;
Combes & Sanders 1981;
Sellwood & Wilkinson
1993).
In an initially axisymmetric
stellar disk, first a transient two-armed spiral wave develops; since it
is trailing, it transfers angular momentum outwards
(Lynden-Bell & Kalnajs
1972).
The bar then forms in two steps: first a short and weak
bar forms, rotating with a high pattern speed which is always
higher than the maximum of the precession rate  -
-  / 2. The
bar, as a wave inside its corotation, has a negative angular momentum,
and is amplified through the outwards transfer provided by the spiral
arms. Then, the bar slows down, with a growing intensity, trapping
more and more particles in its potential well. This can be understood
in the frame of density wave theory as well as in stellar orbit
theory. At the beginning, the perturbation is linear; for the swing
amplifier to work, there should be no inner Lindblad resonance.
This is fulfilled if the bar pattern speed is well over the
/ 2. The
bar, as a wave inside its corotation, has a negative angular momentum,
and is amplified through the outwards transfer provided by the spiral
arms. Then, the bar slows down, with a growing intensity, trapping
more and more particles in its potential well. This can be understood
in the frame of density wave theory as well as in stellar orbit
theory. At the beginning, the perturbation is linear; for the swing
amplifier to work, there should be no inner Lindblad resonance.
This is fulfilled if the bar pattern speed is well over the  -
-  / 2 curve, justifying the
fast rotation at the start.
/ 2 curve, justifying the
fast rotation at the start.
In parallel, we can consider that the bar traps more particles in
extending its length. Those particles, at larger radii, have lower
precession rates, and it is likely that the global equalized rate,
i.e. the pattern speed, will be lowered by the adjunction of these
particles. As the pattern speed decreases, the bar loses angular
momentum through the spiral wave.
Figure 57. Example of bar formation in an
N-body simulation, with stars only. The galaxy is plotted every 200 Myr.
t = 200 Myr

| t = 400 Myr
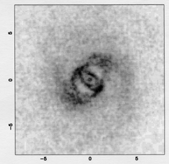
| t = 600 Myr
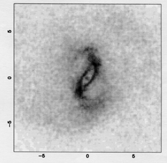
|
t = 800 Myr

| t = 1 Gyr

| t = 1.2 Gyr

|
Periodic orbits are parallel to the bar only inside corotation, as we
shall see below. As  b decreases, corotation propagates
outwards, and the bar extension could be higher. Bar formation by
trapping of orbits is illustrated in the N-body simulation of
Figure 57.
b decreases, corotation propagates
outwards, and the bar extension could be higher. Bar formation by
trapping of orbits is illustrated in the N-body simulation of
Figure 57.



 -
-  / 2) must increase with
specific angular
momentum, a condition that is fulfilled only in the central parts of
galaxies where the velocity curve is rising. The pattern speed of the
bar in this scenario must be lower than the peak of the
/ 2) must increase with
specific angular
momentum, a condition that is fulfilled only in the central parts of
galaxies where the velocity curve is rising. The pattern speed of the
bar in this scenario must be lower than the peak of the
 -
-  / 2 axisymmetric curve, which
is not the case at the
beginning of the bar instability in N-body simulations.
/ 2 axisymmetric curve, which
is not the case at the
beginning of the bar instability in N-body simulations.








