


15. RINGS IN NON-BARRED GALAXIES
The standard mechanism to form rings, as we have described above,
appears to require the presence of a bar. We can note however that in
the presence of a steady spiral density wave, gravity torques will also
drive the gas towards the center inside corotation, and outwards
outside corotation, so that it could accumulate in rings at resonances.
But the mechanism is not efficient, since spirals are not steady enough
in the absence of bars. Recurrent spiral structure has been obtained in
N-body simulations, but always with different pattern speeds (e.g.,
Sellwood & Carlberg
1984).
First, not only do spiral instabilities
heat the stellar medium, which becomes unresponsive, but also angular
momentum is exchanged due to phase-shifts between density and
potential, and rapid evolution occurs. On the contrary, a bar is very
steady and robust in the stellar component.
The existence of rings in nonbarred galaxies is a common phenomenon
(see section 9.1 and
Buta 1995).
Some of them could be explained by the
steady tidal action of a bound companion, since the non-axisymmetric
perturbation is then very similar to that of a bar
(Combes 1988);
these
are described in section 17. Many cases
could also be explained
by the existence of a weak oval distortion, weak enough that the galaxy
is classified SA. A very good example is the case of NGC 7217, an
isolated spiral which appears even on near-infrared photographs very
axisymmetric, and which may be one of the most axisymmetric galaxies
ever observed
(Buta et al. 1995b).
Yet the very faint m = 2 component
discovered in the deprojected image is sufficient to explain the
formation of the three rings observed in the galaxy with resonances.
The nuclear, inner and outer rings of NGC 7217 are well reproduced by a
simulation of gas flow in the potential derived from the I-band image
(Buta et al. 1995b).
A noteworthy characteristic discovered by the
latter authors is a large extended circular halo of light in the
outer parts of the galaxy.
Another possibility for the ringed nonbarred galaxies is that the rings
were formed while the galaxy was barred, but the bar has now been dissolved
through either tidal interaction with a companion, or through gas
accretion and mass concentration. This has been proposed in particular
for NGC 7217
(Verdes-Montenegro et
al. 1995;
Athanassoula 1996),
since
about 20-30% of the stars have been observed in counter-rotation in
this galaxy by
Merrifield & Kuijken
(1994).
The progressive
destruction of the bar could also explain the counter-rotation, through
the librating/rotating separatrix crossing mechanism developed by
Evans & Collett (1994):
in the rotating frame of the bar, some particles
were trapped librating about the bar. When the bar disappears, the
trapped librating orbits are scattered almost equally into clockwise
and anti-clockwise rotating loop orbits. Since not all particles were
trapped with the bar, and due to the preferential sense of rotation,
less than 50% of the stellar population is expected to be
counter-rotating in the final nonrotating frame (which could correspond
to the observed 25%).
If this mechanism is attractive to explain the counter-rotating
phenomena, it raises however some problems for the survival of rings.
The destruction of the bar must not be due to a violent event, because
that would have destroyed also the rings; for this reason, the tidal
action of a companion is not likely (see
section 17). If it is the gas
accretion that makes the galaxy axisymmetric, it must have occurred
quite rapidly, otherwise the changing pattern speed of the decaying bar
would have diluted the rings. But if the axisymmetrization is rapid,
the velocity dispersion produced at the separatrix crossing is too high
(Evans & Collett 1994).
15.1. Bar Destruction, Lens, and Oval
Formation
Recent numerical simulations, and in particular those including the gas
component, have promoted the idea that bars might be only a transient
phase in the life of a galaxy. Bars can be easily destroyed by massive
gas flow towards the center or by a satellite merger, and also can
re-form since spiral disks are cooled down and made unstable to new
perturbations by fresh gas accretion. The duty cycle of the strong bar
phase could be of the order of 30% of the Hubble time, explaining the
observed frequency of SB galaxies. This is in contrast with the view
brought along by previous N-body simulations dealing with only the
stellar component, where the bar is robust and lasts for more than a
Hubble time.
The influence of a central mass concentration on bar strength was first
studied for its relevance to AGN's: a sufficiently massive black hole in
the nucleus of a barred galaxy can weaken and destroy the bar
(Norman et al. 1985;
Hasan and Norman 1990;
Pfenniger & Norman
1990).
The black
hole acts as a scattering mass that can axisymmetrize the central
disk. The bar favors elongated orbits in the center, with less
angular momentum, which are more sensitive to the central mass than
circular orbits. For high enough central masses, stochasticity develops
in the stellar orbital structure, and the bar is no longer supported by
the x1 family of orbits. Through orbit computations,
Hasan & Norman (1990)
have determined the percentage of the remaining regular
x1 orbits, as a function of the black hole mass. This
percentage
falls significantly when the central mass reaches 5% of the total
mass: the percentage of stochastic orbits is so large that the bar is
significantly weakened, then destroyed for a mass fraction of 10%.
Through self-consistent stellar simulations,
Nishida & Wakamatsu
(1996)
have shown that a bar still forms with the same amplitude in a
galaxy with an initial mass concentration as high as 5%, but its
strength weakens in the long run, while a bar with no central mass
concentration keeps its amplitude in a steady state through a Hubble
time.
In normal spiral galaxies, there do not exist massive black holes as
large as 5% of the total mass, i.e. 5 x 109 M . A very
concentrated nucleus or bulge (of mass Mb, and size
ab) could
play the role of the scattering mass, when the scattered velocity is of
the order of the rotational velocity provided by the disk, i.e., v
. A very
concentrated nucleus or bulge (of mass Mb, and size
ab) could
play the role of the scattering mass, when the scattered velocity is of
the order of the rotational velocity provided by the disk, i.e., v
 (GMb / ab)1/2
(GMb / ab)1/2  Vrot, and the ratio of
scale-lengths between the disk and the central mass concentration is
high enough (more than 5 typically). According to a recent compilation
of observed profiles of spiral galaxies
(Courteau et al. 1996),
this scale-length ratio is on average larger than 10; the condition of a
required (M/r) ratio comparable for the bulge and the disk, i.e.,
(M/r)b
Vrot, and the ratio of
scale-lengths between the disk and the central mass concentration is
high enough (more than 5 typically). According to a recent compilation
of observed profiles of spiral galaxies
(Courteau et al. 1996),
this scale-length ratio is on average larger than 10; the condition of a
required (M/r) ratio comparable for the bulge and the disk, i.e.,
(M/r)b  (M/r)d,
translates then in terms of the surface
densities µb
(M/r)d,
translates then in terms of the surface
densities µb  10
µd, which is often observed in
early-type galaxies. Another possibility is that the strong gas infall
driven by the bar produces itself a sufficient mass concentration, as
suggested by simulations (e.g.,
Friedli & Benz 1993).
The fate of these gas concentrations, once star formation has occurred,
is to contribute to the nucleus or bulge component anyway.
10
µd, which is often observed in
early-type galaxies. Another possibility is that the strong gas infall
driven by the bar produces itself a sufficient mass concentration, as
suggested by simulations (e.g.,
Friedli & Benz 1993).
The fate of these gas concentrations, once star formation has occurred,
is to contribute to the nucleus or bulge component anyway.
How fast does the bar destruction occur, and can we recognize such a
phenomenon in the observations? In the case of a satellite merger, the
event can be very sudden, and the effective dissolution of the bar occurs
in about 20 Myr
(Pfenniger 1991);
it might be too rare to be observed,
although it could be recognized through the presence of a close
companion. In the case of gas infall towards the center, it depends
essentially on the amount of gas present and the rate of accretion. If
the latter is high enough, the decoupling of a secondary bar might be
the first step in the dissolution of the primary one
(Friedli & Martinet
1993).
For a milder gas accretion, the bar dissolution can be
a very long phenomenon, because of self-regulation. The processes could
be at the origin of lens formation, and therefore easy to recognize
(cf. Combes 1996).
The regulation comes from the fact that the gas
accretion destroying the bar is driven by the bar itself: in a first
phase, the torques due to the strong initial bar drive the gas inwards,
increasing significantly the central mass concentration. The central
potential is modified, and so are the frequency curves ( ,
,
 -
-  / 2), until the development
of two inner Lindblad
resonances, and the appearance of the family of x2
perpendicular
orbits in the center. This has the effect of weakening the bar in the
very center. Progressively, if the central concentration builds up,
stochasticity extends in the orbital structure, and the fading of the
bar reduces the torques and the gas infall. Part of the gas coming
from the outer parts of galaxies has now time to form stars in the
disk, which re-establishes the mass balance between the nucleus and the
disk. The central mass concentration loses its dynamical efficiency,
and a new strong bar phase can occur through gravitational instability,
which closes the cycle. To have several such cycles in a Hubble time
requires however a substantial mass accretion, i.e., important gas
reservoirs in the outer parts of galaxies (cf.
Pfenniger et al. 1994).
/ 2), until the development
of two inner Lindblad
resonances, and the appearance of the family of x2
perpendicular
orbits in the center. This has the effect of weakening the bar in the
very center. Progressively, if the central concentration builds up,
stochasticity extends in the orbital structure, and the fading of the
bar reduces the torques and the gas infall. Part of the gas coming
from the outer parts of galaxies has now time to form stars in the
disk, which re-establishes the mass balance between the nucleus and the
disk. The central mass concentration loses its dynamical efficiency,
and a new strong bar phase can occur through gravitational instability,
which closes the cycle. To have several such cycles in a Hubble time
requires however a substantial mass accretion, i.e., important gas
reservoirs in the outer parts of galaxies (cf.
Pfenniger et al. 1994).
The bar destruction process affects the orbital structure in such a way
as to explain lens formation
(Combes 1996).
The main effect is to introduce
stochasticity in the middle of the bar: close to the central mass
concentration, the potential becomes axisymmetric and orbits remain regular;
near the end of the bar, the bar potential is dominant, and the
x1
periodic orbits remain almost unperturbed. The chaotic region
develops in the middle, corresponding to intermediate energies in the rotating
frame. These orbits do not support the bar, and may contribute to a
lens component. The regular orbits still trapped in the bar near its
end might be at the origin of ``ansae'' condensations, that are sometimes
observed in weak bars.
Chaotic orbits are bounded only by their limiting energy curve; in the
bar rotating frame, the effective potential is  (r) - 1/2
(r) - 1/2  2 r2, and is maximum at
corotation. This plays the role of the last
boundary for the chaotic region inside CR. Orbits with higher energies
will eventually escape. This could be the origin of the sharp cut-off
of the lens (e.g.,
Kormendy 1984).
The observation that the lens and
the bar have typically the same maximum size (the bar fills the lens
along its intrinsic major axis) suggests that the lens ends also near
corotation. An exception could be ESO 565-11, where the bar and lens
are misaligned by 60°
(Buta et al. 1995a).
2 r2, and is maximum at
corotation. This plays the role of the last
boundary for the chaotic region inside CR. Orbits with higher energies
will eventually escape. This could be the origin of the sharp cut-off
of the lens (e.g.,
Kormendy 1984).
The observation that the lens and
the bar have typically the same maximum size (the bar fills the lens
along its intrinsic major axis) suggests that the lens ends also near
corotation. An exception could be ESO 565-11, where the bar and lens
are misaligned by 60°
(Buta et al. 1995a).
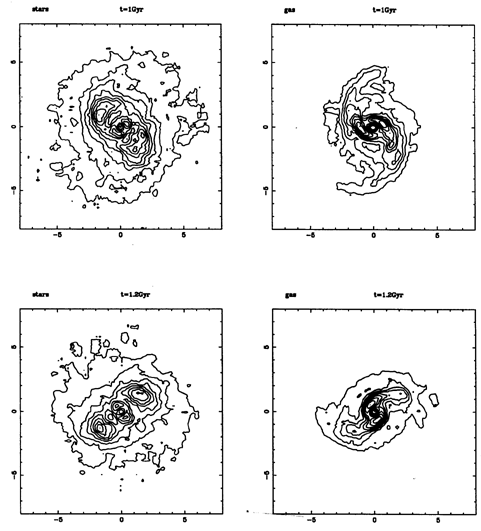
Self-consistent simulations with stars and gas of the slow bar
destruction by a central mass concentration illustrate the lens
formation (Figure 83). In this particular
case, the central
mass concentration is 1% and the total gas mass is 0.5% of the total
mass. A very thick oval forms through dissolution of the stellar bar,
with the ``ansae''-shape. The gas bar is thinner and longer. The
half-destroyed bar remains for a 2 x 109 yrs time-scale.
Figure 83. Isophotes of the results
of N-body simulations with stars (left) and gas (right), starting with
axisymmetric conditions, and a mass concentration of 1%. The bar stays
half-dissolved for a time-scale of Gyrs. Note the ``ansae'' in the stellar
distribution.
|



 . A very
concentrated nucleus or bulge (of mass Mb, and size
ab) could
play the role of the scattering mass, when the scattered velocity is of
the order of the rotational velocity provided by the disk, i.e., v
. A very
concentrated nucleus or bulge (of mass Mb, and size
ab) could
play the role of the scattering mass, when the scattered velocity is of
the order of the rotational velocity provided by the disk, i.e., v
 (GMb / ab)1/2
(GMb / ab)1/2  Vrot, and the ratio of
scale-lengths between the disk and the central mass concentration is
high enough (more than 5 typically). According to a recent compilation
of observed profiles of spiral galaxies
(Courteau et al. 1996),
this scale-length ratio is on average larger than 10; the condition of a
required (M/r) ratio comparable for the bulge and the disk, i.e.,
(M/r)b
Vrot, and the ratio of
scale-lengths between the disk and the central mass concentration is
high enough (more than 5 typically). According to a recent compilation
of observed profiles of spiral galaxies
(Courteau et al. 1996),
this scale-length ratio is on average larger than 10; the condition of a
required (M/r) ratio comparable for the bulge and the disk, i.e.,
(M/r)b  (M/r)d,
translates then in terms of the surface
densities µb
(M/r)d,
translates then in terms of the surface
densities µb  10
µd, which is often observed in
early-type galaxies. Another possibility is that the strong gas infall
driven by the bar produces itself a sufficient mass concentration, as
suggested by simulations (e.g.,
Friedli & Benz 1993).
The fate of these gas concentrations, once star formation has occurred,
is to contribute to the nucleus or bulge component anyway.
10
µd, which is often observed in
early-type galaxies. Another possibility is that the strong gas infall
driven by the bar produces itself a sufficient mass concentration, as
suggested by simulations (e.g.,
Friedli & Benz 1993).
The fate of these gas concentrations, once star formation has occurred,
is to contribute to the nucleus or bulge component anyway.



 ,
,
 / 2), until the development
of two inner Lindblad
resonances, and the appearance of the family of x2
perpendicular
orbits in the center. This has the effect of weakening the bar in the
very center. Progressively, if the central concentration builds up,
stochasticity extends in the orbital structure, and the fading of the
bar reduces the torques and the gas infall. Part of the gas coming
from the outer parts of galaxies has now time to form stars in the
disk, which re-establishes the mass balance between the nucleus and the
disk. The central mass concentration loses its dynamical efficiency,
and a new strong bar phase can occur through gravitational instability,
which closes the cycle. To have several such cycles in a Hubble time
requires however a substantial mass accretion, i.e., important gas
reservoirs in the outer parts of galaxies (cf.
/ 2), until the development
of two inner Lindblad
resonances, and the appearance of the family of x2
perpendicular
orbits in the center. This has the effect of weakening the bar in the
very center. Progressively, if the central concentration builds up,
stochasticity extends in the orbital structure, and the fading of the
bar reduces the torques and the gas infall. Part of the gas coming
from the outer parts of galaxies has now time to form stars in the
disk, which re-establishes the mass balance between the nucleus and the
disk. The central mass concentration loses its dynamical efficiency,
and a new strong bar phase can occur through gravitational instability,
which closes the cycle. To have several such cycles in a Hubble time
requires however a substantial mass accretion, i.e., important gas
reservoirs in the outer parts of galaxies (cf.
 (r) - 1/2
(r) - 1/2 