|



16. INTERACTIONS BETWEEN SEVERAL WAVES
The co-existence of several rings in the same barred galaxy, with relative radii compatible with what is expected for the various Lindblad resonances, speaks against the existence of several patterns with different angular speeds in the galaxy. However, for certain peaked mass distributions, with high gradients of rotation frequencies, the whole spiral disk cannot participate in the same pattern, as shown in N-body simulations (Sparke & Sellwood 1987). Several pattern speeds can then co-exist, with non-linear interactions between the various waves (Tagger et al. 1987), so that mutual amplification can occur. The most frequent interactions will concern two m = 2 patterns (for instance a primary bar, and a nuclear bar or spiral), that interact at a common resonance (for example, the corotation of the nuclear pattern coincides with the ILR of the bar). In the overlap region, beat waves with multiplicity m equal to the sum and the difference of the two m = 2 modes, i.e. m = 0 and m = 4, will be generated, and their pattern speeds will be such that the overlapping region is also their OLR and ILR, respectively. The application of this mechanism to real galaxies could explain the observations of nuclear bars just inside nuclear rings, with arbitrary orientation.
16.1. Nuclear Bars inside Nuclear Rings
The presence of a possible second component in the center of barred galaxies has been recognized very early through the presence of a secondary bar (distinct position angle, and distinct ellipticity) in the photometry, or through central isophote twists. Already de Vaucouleurs (1974) had noticed such ``bars within bars'', and Sandage & Brucato (1979) high surface brightness nuclear bars, as independent entities. Kormendy (1982b) found that isophote twists are preferentially found in SB galaxies with strong central concentration, and that the second small bar is aligned nearly perpendicular to the main bar; he proposed that the triaxiality of bulges is the cause of the projected twists. More recently, Buta & Crocker (1991), Shaw et al. (1993), Wozniak et al. (1995), and Friedli et al. (1996) have shown that these twists are associated with nuclear rings, clearly traced by B - I, B - V, and even J - K color index maps. The nuclear ring is always encircling the nuclear bar; sometimes the nuclear ring is itself elongated almost perpendicular to the main bar. These are cases where the twists cannot be attributed to a triaxial bulge seen in projection. Similar phenomena have been observed in the molecular component (e.g., Devereux et al. 1992, Kenney et al. 1992). Molecular bars perpendicular to the main bar are observed inside a nuclear ring. Sometimes only two peaks are prominent in the CO emission, at the crossing of the leading dust lanes parallel to the bar, and the smaller nuclear ring. These twin-peaks (Kenney 1991) represent the crossing zone between the x1 and x2 types of orbits.

|
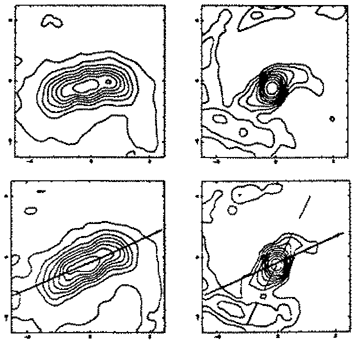
Two main interpretations have been proposed for these isophote twists: first, in the presence of two inner Lindblad resonances, the family x2 of perpendicular periodic orbits is the cause of phase-shifts in the gas component (Shaw et al. 1993); once enough gas is gathered in the center, a fraction of the stellar component follows its potential. This configuration remains for a short time, since strong gravity torques are present. Second, a nuclear bar can decouple from the main bar, with a larger pattern speed, as suggested by Shlosman et al. (1989), and simulated by Friedli & Martinet (1993). In that case, no preferential orientation is expected between the two bars, which represents better the observations (Buta & Crocker 1993). In both cases, this nuclear phenomenon requires a large mass concentration and large gradients of rotational velocities in the center, in order that there exist 2 ILR's. It requires also a significant gas fraction in the center, since a pure stellar disk will be too hot to participate in a second central pattern. Pure stellar N-body simulations do not reveal the nuclear bar decoupling, but a global gas mass fraction of 6% is enough to cool down the center, so that it can show this second pattern. The physical properties of the gas and the amount of dissipation assumed are the essential factors that determine the dynamical behavior between the two mechanisms outlined above (Combes 1994). With a small amount of dissipation, the gas settles in a phase-shifted bar, influenced by the existence of perpendicular periodic orbits (Figure 84), while with a more viscous gas model, a rapidly rotating nuclear bar of stars and gas decouples from the main bar (Figure 85). In the simulations, where the nuclear bar rotates more rapidly than the primary bar, the corotation of the nuclear bar corresponds roughly to the ILR of the primary, so that the non-linear coupling between the two bars might be at work (Tagger et al. 1987).

|
Since the phase-shift between the gas density and the total potential is minimized in the case of the decoupled fast-rotating nuclear bar, gravity torques, and therefore gas infall, are also minimized, so that the nuclear bar phase is less transient than the isophote twists phase. The nuclear bar can survive a few rotations of the primary, which explains its frequent observation.