


2.2.2 The luminosity function of galaxies
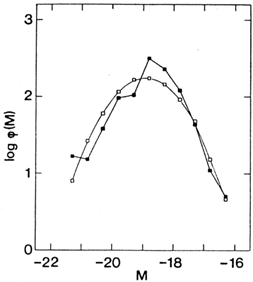
A first attempt to find the luminosity function of extragalactic objects was made by Wirtz in 1926. His tabulated values can be used to construct the diagram shown in Fig. 14. His magnitude scale, which is much closer to the modern one than those of other astronomers of his time, is based on diameter measurements. The distribution is Gaussian, as was also found by Lundmark (1927) and Hubble and Humason (1931). Wirtz, using the measurements of Fath (1914), points out the shortcomings, unavoidable at this early stage of investigations:
``The luminosity curve cannot yet be transformed to unit space. Among other things, the limit of the observed space is not known, irrespective of the way of fixing the absolute measuring scale.''
|
Figure 14. A reconstruction of the first
luminosity function
(Wirtz 1926).
|
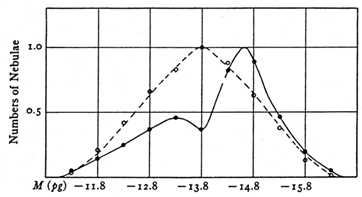
While the luminosity function (LF) determined by Hubble and Humason (1931) is a Gaussian distribution of absolute magnitudes for the cluster nebulae, an asymmetric curve is found for isolated nebulae. The authors consider the latter effect to be at least partly due to selection. The original LF is shown in Fig. 15. The LF was also considered Gaussian by numerous subsequent authors (including Zwicky in 1933), at least, it was assumed that the LF has a maximum at a certain luminosity.
|
Figure 15.
Hubble and
Humason's (1931)
luminosity function.
|
An exponential luminosity function was given by Zwicky (1957):
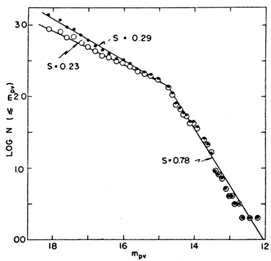
Figure 16.
Abell's (1962)
luminosity function.
Figure 17.
Schechter's (1976)
luminosity function.
Other LFs were to follow, e.g. Abell's luminosity function shown in
Fig. 16 (see also references in
Schechter 1976).
What was to become
known as the Schechter function is double exponential when expressed
in terms of absolute magnitude (Fig. 17):
``We investigate the expression
where
Recently, evidence has been accumulated by
Sandage et
al. (1985),
that
the Schechter function is the envelope of the individual Gaussian
distributions of galaxies in different luminosity classes, possibly
excepting very faint dwarf galaxies.
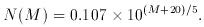

``Best fit of analytic expression to observed composite cluster
luminosity distribution. Filled circles show the effect of including
cD galaxies in composite.''
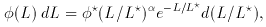

 , L
, L , and
, and  are parameters to be determined
from the data. The
parameter
are parameters to be determined
from the data. The
parameter 
 is a number per unit volume,
and L
is a number per unit volume,
and L is a
`characteristic
luminosity' (with an equivalent `characteristic magnitude',
M
is a
`characteristic
luminosity' (with an equivalent `characteristic magnitude',
M ) at
which the luminosity function exhibits a rapid change in the slope in
the (log
) at
which the luminosity function exhibits a rapid change in the slope in
the (log  , log
L)-plane. The existence of such a characteristic
magnitude has long been stressed by Abell
(1962,
1965
- his LF is the
approximation of the measured distribution by two lines of different
slope, intersecting at M
, log
L)-plane. The existence of such a characteristic
magnitude has long been stressed by Abell
(1962,
1965
- his LF is the
approximation of the measured distribution by two lines of different
slope, intersecting at M ), and his notation M
), and his notation M has been pirated for
the present discussion. The dimensionless parameter
has been pirated for
the present discussion. The dimensionless parameter  gives the slope
of the luminosity function in the (log
gives the slope
of the luminosity function in the (log  , log L)-plane when L << L
, log L)-plane when L << L .''
.''