2.3.2 Evolution of clustering and N-body simulation

No generally accepted answer has been found as yet to the question: What causes clustering?

One of the early hypotheses dates back to Lemaître (1934) who suggested a mechanism for the growth of small fluctuations around the mean values of density and velocity in the expanding universe, using the concept that both density and velocity are coupled to `cosmic repulsion', represented by the cosmological constant (Sect. 4.1). The said fluctuation may locally retard or even reverse the general expansion.

``For the perturbed motion, i.e., for a distribution of mass and initial velocities somewhat different from the [perfectly homogeneous] idealized model, the motion at some places may be of a completely different type from the notion of the idealized model. The relation between the energy constant h and the mass m may be such that the motion is of the collapsing type . . .
Occasionally, we may also have equilibrium regions. The fact that such an equilibrium region is unstable means only that it will occur relatively rarely and that the collapsing regions will be decidedly more frequent than equilibrium-regions. The hypothesis we wish to discuss is that collapsing regions must be identified with the extra-galactic nebulae and the equilibrium-regions with the clusters of nebulae.''

In the same paper he made another interesting statement not directly connected to the present discussion:

``The differences of nebulae may be accounted for as a difference of total total angular momentum of the collapsing regions.''

Lemaître concluded:

``We may expect to get a complete theory of all the problems connected with extragalactic nebulae by applying statistical mechanics to small inhomogeneity in our idealized model. Such an investigation would probably involve only two parameters, one to fix the mean velocity of expansion at the instant of equilibrium, a second one to define the dispersion of the distribution of matter from the idealized model.''

Another statistical approach is N-body simulation, a technique which helps to also find evidence concerning the history of clustering. The numerical experiment consists of three parts: the process to be tested is chosen and presented in mathematical form, numerical values for the relevant parameters are inserted, integration over a predetermined interval is carried out. An early numerical experiment to explain the formation of double and multiple galaxies was performed by Holmberg in 1940. The process is capture, invoked through tidal interaction. The parameters and results are shown in Fig. 21.

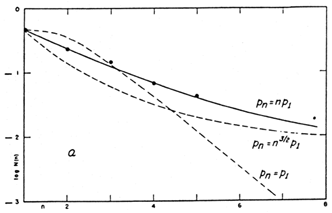
Figure 21. Holmberg's (1940) results. ``Distribution of nebulae (relative number = N(n)) in systems of different order (n). The dots represent observed numbers, whereas the curves give theoretical distributions corresponding to different assumptions for the `captureability' (pn) of systems of different order.''

In a subsequent experiment Holmberg (1941) uses an analogue device to test tidal interaction itself. Each one of two galaxies consists of 37 particles.

``A study of tidal disturbances is greatly facilitated if it can be restricted to two dimensions... In order to reconstruct the orbit described by a certain mass element belonging to one of the two nebulae, we must first derive as a function of time the x and y components of the total gravitational force acting upon the element. Starting from a certain distribution of mass in the nebulae, we may find the total gravitation by a purely numerical integration. However such an integration is impracticable on account of the large amount of work involved. In the present case a solution has been found by replacing gravitation by light. Every mass element is represented by a small light bulb, the light being proportional to the mass, and the total light along the x and y axes is measured by a combination of a photocell and a galvanometer. The measured values represent the components of the gravitational force. The latter components are obtained by adding up the attractions due to individual mass elements, each multiplied by the cosine of the corresponding projection angle. Consequently the photocell must obey the cosine law as far as the angle of incidence of the light is concerned. If the photocell obeys the cosine law and if the combination of photocell and galvanometer gives a linear relation between light and scale reading, the galvanometer deflection will be proportional to the total gravitational force or, more correctly, to the total acceleration.''

For an extensive discussion of Holmberg's extragalactic work, see Rood (1987).

The availability of fast computers solved the problem of tedious integrations and made numerical simulations a standard technique in clustering studies. A recent review article (Sellwood 1987) describes its potential if proper care is taken in the handling and interpretation of simulations with the large numbers of particles which are now within reach. The computation of the evolution of clustering has become a standard tool in cosmology.

There is also a close connection between the early models of Holmberg and the extensive calculations by Toomre and Toomre (1972), which are in turn considered to be the basis for modern concepts of merging and induced star formation, i.e. starbursts in galaxies. The latter has become important especially in the context of infrared emission of heated dust in these systems.