All observations show that the universe is baryon-antibaryon asymmetric, and that there is negligible primordial antimatter in our observable universe [Steigman(1976)]. To obtain a quantitative measure of this asymmetry we look to the standard cosmological model. One of the major successes of cosmology is an accurate prediction of the abundances of all the light elements; a calculation which requires a single input parameter, the baryon to entropy ratio
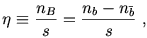
| (1) |
where nb is the number density of baryons,
n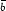
is that
of antibaryons, and s denotes the entropy density. If one
compares calculations of elemental abundances with observations,
then there is agreement between these numbers if
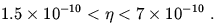
| (2) |
This number is an input parameter in the standard model of cosmology, and it is one of the goals of particle cosmologists to understand its origin from particle physics.
In 1968, Sakharov [Sakharov(1967)] identified the conditions necessary for a particle physics theory to generate any asymmetry between baryons and antibaryons. These are violations of the baryon number (B), the charge (C) and charge-parity (CP) symmetries, and a departure from thermal equilibrium. One can imagine (any many have) a great number of ways in which this combination of circumstances could be arranged in the context of particle physics in an expanding universe. However, it seems fair to devote most attention to those mechanisms which arise as a natural consequence of particle physics theories proposed for other compelling phenomenological reasons. In addition, those mechanisms amenable to experimental tests in the near future, particularly electroweak baryogenesis, deserve our immediate attention (for reviews see [Riotto and Trodden(1999), Riotto(1998), Trodden(1999), Rubakov and Shaposhnikov(1996), Cohen et al.(1993), Dolgov(1992)]).
Certainly, the original suggestion that grand unified theories (GUTs) may be responsible for the BAU is firmly in the first category, but probably not in the second. Grand unification is an attractive idea for understanding the origin of the standard model, the apparent meeting of the running SU(3), SU(2) and U(1) couplings, and the quantization of charge. Further, baryon number is naturally violated in GUT models because quarks and leptons lie in the same representation of the grand unified gauge group, and C and CP may also naturally be violated. The required departure from thermal equilibrium must have an entirely cosmological origin, and in this case it occurs because the expansion rate of the universe at the GUT epoch is significantly faster than the rate of particle interactions. However, despite its attractive properties, there are an number of problems to be overcome by such models. While this is not the place to provide a detailed treatment of these, one is particularly relevant to our subsequent discussion.
The electroweak theory itself violates baryon number (and to an identical amount lepton number (L)) through an anomaly ['t Hooft(1976)]. While this is irrelevant at zero temperature (since the relevant phenomenon is mediated by an instanton of large action, and hence has a close to vanishing rate), at temperatures around or above the electroweak scale such events are unsuppressed and copious [Kuzmin et al.(1985)]. One consequence of this is that if a GUT model does not produce a net baryon minus lepton number (B-L) asymmetry rather than just a baryon asymmetry, then anomalous electroweak interactions between the GUT and electroweak scales will erase the asymmetry. However, the presence of baryon number violation in the electroweak theory at finite temperature suggests that this theory itself may be capable of generating the BAU [Shaposhnikov(1986), Shaposhnikov(1987), Shaposhnikov(1988), Cohen and Kaplan(1987), Cohen and Kaplan(1988), Cohen et al.(1990), Cohen et al.(1991a), Cohen et al.(1991b), Nelson et al.(1992), Turok and Zadrozny(1990), Turok and Zadrozny(1991)]. Of course, there are two other Sakharov conditions to be satisfied. In the standard model the condition of C violation is maximal and CP violation is present at a small level (as evidenced in the Kaon system). However, even if the level of CP violation were enough (which it is not) there is insufficient departure from thermal equilibrium at the electroweak scale, since the minimal electroweak phase transition is continuous for Higgs masses is the experimentally allowed range. This observation has led to the hope that the minimal supersymmetric standard model (MSSM) may allow for electroweak baryogenesis.
The behavior of the electroweak phase transition in the minimal
supersymmetric standard model is dependent on the mass of the
lightest Higgs particle, and the mass of the top squark. A variety of
analytical
[Carena et
al.(1996),
Delepine et
al.(1996),
Espinosa(1996),
Bodeker et
al.(1997),
Losada(1997),
Farrar and
Losada(1997),
de Carlos and
Espinosa(1997),
Carena et
al.(1998),
Losada(1999)]
and lattice
[Laine(1996),
Laine and
Rummukainen(1998a),
Cline and
Kainulainen(1996),
Laine and
Rummukainen(1998b)]
computations have revealed that the
phase transition can be sufficiently strongly first order in the
presence of a top squark lighter than the top quark. In order to
naturally suppress contributions to the
-parameter, and
hence preserve a good agreement with precision electroweak
measurements at LEP, the top squark should be mainly right handed.
This can be achieved if the left handed stop soft supersymmetry
breaking mass mQ is much larger than MZ.
The preservation of the baryon number asymmetry requires the
order parameter
<
(Tc)>
/ Tc to be larger than
one. In order to obtain values of
<(Tc)>
/ Tc larger
than one, the Higgs mass must take small values, close to the
present experimental bound. Hence, small values of
tan
are preferred. The larger the left handed stop mass, the closer to
unity tan
must be. This implies that the left handed stop
effects are likely to decouple at the critical temperature, and
hence that mQ mainly affects the baryon asymmetry
through the resulting Higgs mass. A detailed analysis, including all
dominant two-loop finite temperature corrections to the Higgs
effective potential and the non-trivial effects arising from
mixing in the stop sector, has been performed
[Carena et
al.(1998)],
and the region of parameter space for which MSSM electroweak baryogenesis
can happen identified. Taking into
account the experimental bounds as well as the requirement of
avoiding dangerous color breaking minima, it was found that the
lightest Higgs should be lighter than about 105 GeV, while the
stop mass may be close to the present experimental bound and must
be smaller than, or of order of, the top quark mass
[Carena et
al.(1998),
Laine and
Rummukainen(199a)].
This lower
bound has been essentially confirmed by lattice simulations
[Laine and
Rummukainen(1998b)],
providing a motivation for the search for Higgs and
stop particles at the Tevatron and future colliders.
The popularity of this idea is tightly bound to its testability. The physics involved is all testable in principle at realistic colliders. Furthermore, the small extensions of the model involved to make baryogenesis successful can be found in supersymmetry, which is an independently attractive idea, although electroweak baryogenesis does not depend on supersymmetry. The most direct experimental way of testing this scenario is through the search for the lightest Higgs. In this sense, we are close to knowing whether electroweak processes were responsible for the BAU.
If the Higgs is found, the second test will come from the search for the lightest stop at the Tevatron collider. If both particles are found, the last crucial test will come from B physics, more specifically, in relation to the CP-violating effects.
Moreover, the selected parameter space leads to values of the
branching ratio
BR(b
s
)
different from
the Standard Model case. Although the exact value of this
branching ratio depends strongly on the value of the µ and
At parameters, the typical difference with respect to the
Standard Model prediction is of the order of the present
experimental sensitivity and hence in principle testable in the
near future. Indeed, for the typical spectrum considered here, due
to the light charged Higgs, the branching ratio BR(b
s)
is somewhat higher than in the SM case,
unless negative values of Atµ are
present. The crucial nature of
knowledge concerning CP violation in the B-sector for
baryogenesis means that the results of the BaBar
[bab(1995)],
BTeV [bte(2000)]
Belle [bel(1995)] and
LHCb [lhc(1998)]
experiments, for example the BaBar measurement of
sin(2)
[Aubert et
al.(2001)]
announced during the Snowmass meeting, will be particularly useful.
We now turn to a third baryogenesis scenario, that has received a
lot of attention. This mechanism was introduced by Affleck and
Dine (AD)
[Affleck and
Dine(1985)]
and involves the cosmological
evolution of scalar fields carrying baryonic charge. These scenarios are
most naturally implemented in the context of
supersymmetric models (e.g.
[Dine et
al.(1996)]).
Consider a colorless, electrically neutral combination of quark
and lepton fields. In a supersymmetric theory this object has a
scalar superpartner, 
,
composed of the corresponding squark
and slepton
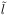fields.
Now, an important feature of
supersymmetric field theories is the existence of "flat
directions" in field space, on which the scalar potential
vanishes. Consider the case where some component of the field
lies along a flat
direction. By this we mean that there
exist directions in the superpotential along which the relevant
components of can be
considered as a free massless field.
At the level of renormalizable terms, flat directions are generic,
but supersymmetry breaking and nonrenormalizable operators lift
the flat directions and sets the scale for their potential.
During inflation it is natural for the
field to be displaced from
the position
<> = 0, establishing
the initial
conditions for the subsequent evolution of the field. An important
role is played at this stage by baryon number violating operators
in the potential V(),
which determine the initial phase of
the field. When the Hubble rate becomes of the order of the
curvature of the potential, the condensate starts
oscillating around its minimum. At this time,
B-violating terms in the potential are of comparable importance
to the mass term, thereby imparting a substantial baryon number to
the condensate. After this time, the baryon number violating
operators are negligible so that, when the baryonic charge of
is transferred to fermions
through decays, the net baryon
number of the universe is preserved by the subsequent
cosmological evolution.
The challenges faced by Affleck-Dine models are combinations of those faced by the GUT and electroweak ideas. In particular, it is typically necessary that B - L be violated along the relevant directions and that there exist new physics at scales above the electroweak. If supersymmetry is not found, then it is hard to imagine how the appropriate flat directions can exist in the low energy models.
Of all models for baryogenesis, the electroweak scenario has received most attention. Electroweak baryogenesis is such an attractive idea because it is testable and uses physics that is already there for a good particle physics reason. If the model is successful, it is a triumph of the particle physics/cosmology union. If not, our primary attention should be focused on models with the same properties. It is possible that Affleck-Dine models may fit the bill, or that the discovery of neutrino masses is telling us something useful about the direction to go