The major breakthrough in our understanding of the curious ring galaxies came from two sources, namely the work of Lynds and Toomre (1976), and Theys and Spiegel (1977). In both cases ring galaxies were hypothesized to be the result of a head-on collision between a compact companion galaxy and a larger disk system. The resulting gravitational perturbation was shown to generate rings in the disk of the larger system. The backdrop to this rather startling idea was the earlier pioneering work on tidal interactions of Toomre and Toomre (1972) who had already begun to destroy the myth of the permanence of large scale galactic structure over a Hubble time. A common feature of the collisional ring formation picture is the generation of radially expanding density waves resulting from the crowding of stars in the disk. (A more complete description of the kinematics and dynamics is presented in Section 4.) Although the most coherent effects are likely to be found in the dynamically cool disk stars and gas, the central perturbation will also have consequences for the halo stars and any dark matter present.
Lynds and Toomre (1976) first presented the elegant conceptual model that forms the basis of our understanding of the ring galaxy phenomenon. In the simplest form of this model, a small companion galaxy is assumed to pass down the symmetry axis of the larger primary galaxy, and move through the disk center. Prior to the collision the stars in the primary disk are assumed to be in circular orbits. At the time of impact the disk stars feel a strong pull toward the center as a result of the companion's gravity. (Note: the cross section of each star is so small that virtually all of the stars in the two galaxies will pass by each other in the "collision"). In the simplest case we also assume that the collision is so rapid that the disk stars do not have time to adjust to the sudden inward impulse. Specifically, in the so-called impulse approximation (IA), the stellar positions are assumed to be the same immediately before and after the collision, but after the collision each star has acquired an inward radial velocity (see e.g., Tremaine 1981). As long as the perturbation is not too large, the resulting stellar orbits in the disk can be well approximated by radial epicyclic oscillations about a guiding center, i.e., the precollision orbit. Lynds and Toomre graphically illustrated this with the example of planetary orbits following a hypothetical near collision between the Sun and another star. This solar system example also reminds us of the ancient origin of epicycles as the simplest modification of "perfect" circular orbits.
Once we assume that the perturbing force only affects the disk stars for a short time, then subsequent motions are purely kinematic. Specifically, this kinematic approximation neglects the effects of the self-gravity of the perturbation. It is especially appropriate for collisions with large relative velocities (e.g., such as probably occur in galaxy clusters). The kinematic approximation assumes a decoupling of the perturbation from the resulting motions without specifying how the perturbation is derived.
After the companion passes through, the disk, individual stars begin
their epicyclic oscillations. In general, the period of these
oscillations increases with radius throughout most of the disk. For
example, in a flat rotation curve disk the epicyclic frequency scales
as 
v/r, so the period scales as
P
r. Thus, while the stars at
a given radius have rebounded and begun to move outwards, those at a
slightly larger radius are still moving inwards. The consequence of
this radial dispersion is that stellar orbits will bunch or crowd at
some radii, yielding high densities there (see
Toomre 1978).
At other
radii the orbits spread, giving rise to rarefied regions. These
effects are well demonstrated by radius versus time diagrams.
Figure 3
shows the first such used for ring galaxies by
Toomre (1978).
The region of orbit crowding propagates outward as a density wave.
|
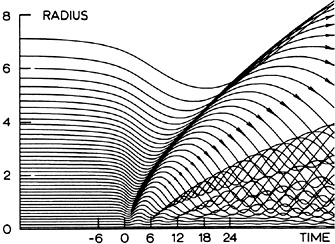
Figure 3. Radial trajectories of 40 particles from the symmetrical encounter model of Toomre (1978). The crowding of the particles into the "rings" is clearly demonstrated in this pioneering model. |
Figure 3 illustrates several other important points. In the first ring the orbit crowding occurs almost exclusively among particles rebounding outward. It also shows that a determination of the outflow velocity of an individual star or HII region in some part of the first ring probably gives a good indication of the outflow of all of the material in that region. In the second ring, infalling and outflowing stars cross each other in a sharply defined high-density region with sharp caustic edges. This is a qualitatively different behavior, and will be further examined in Section 4. In this case, determining ring propagation speeds from individual stellar, HII region or gas cloud radial velocities is much more problematic.
The orbit crossing zones become wider in later rings, and they overlap each other. This radial phase mixing, together with the fact that the later rings include ever fewer stars, eventually renders the rings indistinguishable and ultimately invisible. There are a couple of caveats, however. First, even at very late times, the simple models indicate that individual rings can separate out at large radii. Secondly, even when the rings overlap, some memory of the collision is retained in the continuity of epicyclic phases with radius. Eventually collisional diffusion, through interactions between stars and massive molecular clouds, will erase this memory too.
Thus far, we have only considered perturbations to stellar orbits within the initial plane of the primary disk. This is justified because the perturbations perpendicular to the disk plane (i.e. in the "z" direction) are second order in the radial perturbation amplitude in the impulse approximation. The companion pulls the stars upward in the z direction when it approaches from above, and downward after it passes through. On the other hand, in-plane radial impulses are first order. This is because the companion pulls disk stars radially inward, towards the galaxy's center, when it is both above and below the plane. Yet in the z-direction, even second order effects can be important, especially when the companion is massive and moving slowly. Numerical simulations show several very interesting effects. One example is a vertical tidal effect that was well illustrated by Lynds and Toomre's (1976) Figure 5, reproduced in Figure 4. This figure shows that, as the companion approaches, stars in the central regions of the primary are pulled up towards it more that stars in the outer disk. Similarly, once the companion passes through the primary, stars near the center follow it downward while the outer disk stars are still moving upwards. Viewed edge-on the outer disk appears to nap like a bird's wings relative to the primary center. In conventional terms this leads us to expect a significant warping of the disk in any relatively young ring galaxy. Indeed, there is evidence from simulations (Appleton and James, unpublished) that the flapping can become so vigorous that stars in the outermost disk can be shaken off.
|
Figure 4. The first numerical simulations of collisional ring galaxies (Lynds and Toomre, 1976). The companion mass is 2/3 of the target mass, and "time is reckoned in units of (r03 / GM)1/2", where M is the target mass, and the scale length r0 is shown. |