4.1.2. Symmetric Ring Caustics in the Kinematic Orbit Approximation

In this subsection we will work through a simple example of the analytic theory of nonlinear disk waves. The goal is to derive a simple picture of how the structure and spacing of the rings depends on the structure of both primary and secondary galaxies and their mass ratio. Basic scaling equations will be derived in this section and limiting cases will be discussed. To begin, we adopt the following simplifications:

1. We consider only cylindrically symmetric collisions which generate circular waves in the (infinitely thin) disk. (The case of slightly asymmetric collisions is considered in Appendix 2).

2. We assume that the primary galaxy has a rigid potential, such that the disk rotation curve has the form,

(4.1)

and where is a disk scale length, v() is the rotation velocity at the radius r = , and M() is the (spherically distributed halo) mass contained within the radius r = .

In this example we will generally follow the derivations of Struck-Marcell and Lotan (1990) and Gerber and Lamb (1994) see also Struck-Marcell and Higdon (1993). In Struck-Marcell and Lotan (1990) the primary galaxy was assumed to have a rigid softened point-mass (or related) potential, while Gerber and Lamb assumed a Plummer potential for the companion (and a flat rotation curve primary). These particular potentials were chosen to provide fairly realistic representations of the two galaxies, but they lead to algebraic expressions that are unnecessarily complicated far the present purposes. Here we will stick to tractable power-law forms. Moreover, rings are generally contained within an annulus that only covers a fraction of the disk, and so it is likely that both the potential of the primary and the radial form of the perturbation can be well approximated by a power-law in that region.

The gravitational acceleration which gives the rotation curve of Equation (4.1) is

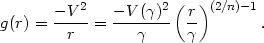
(4.2)

The corresponding mass distribution is

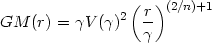
(4.3)

The radial epicyclic frequency is given by the equation (see Binney and Tremaine 1987, Section 3.2.3)

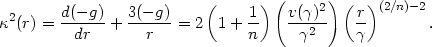
(4.4)

These equations define the structure of the primary galaxy. The perturbed radial orbits are given by

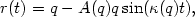
(4.5)

where q is the initial unperturbed orbital radius, and the second term describes the epicyclic oscillations of amplitude A(q). The sinusoidal form of the second term is appropriate for small amplitude oscillations.

3. We assume that A < 1 throughout the disk. The radial velocity is obtained by differentiating Equation (4.5) with respect to time,

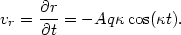
(4.6)

For constant these equations describe simple bulk (solid-body) oscillations of the disk. For the more general radially dependent they describe propagating waves.

We should explicitly state another assumption -

4. that the amplitude A is time independent. Then we must consider the initial conditions. In the IA, t = 0 at the moment of impact, and v_r(t = 0) = v_r(q), where the latter is the radial velocity impulse calculated from the IA (see references above). Then Equation (4.6) can be solved for A,

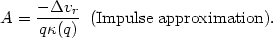
(4.7)

All that remains to complete the analytic model is an explicit expression for the oscillation amplitude. We will not discuss the specific forms of these functions that correspond to well-known analytic galaxy potentials. Instead we will simply assume:

5. a power-law form for the amplitude A,

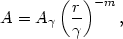
(4.8)

We emphasize that all the structural information about the companion (e.g., mass and compactness), and the orbital parameters (e.g., the relative velocity) are contained in this expression.

Assuming conservation of mass in a thin annulus we find that the local density in the disturbed primary disk is given by

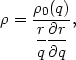
(4.9)

where ₀(q) is the initial, unperturbed density profile. More generally, in regions with multiple star streams we have

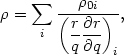
(4.10)

where the sum is over all of the streams. Caustics occur where r / q = 0, implying . With the orbit Equation (4.5) and our adopted forms for and A, we can now derive an explicit form for this caustic condition,

or,

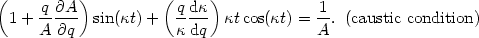
(4.11)

Using Equations (4.4) and (4.8) both of the first two terms can be simplified,

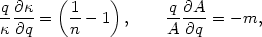
(4.12)

Then the caustic condition becomes

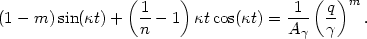
(4.13)

This is the key equation for the caustics. The left-hand-side is in terms of a time-like quantity, the epicyclic phase t, and the right is a function of the dimensionless Lagrangian radius on the caustic edge. For any time t, equation (4.13) can be solved (numerically) for the values of q at the inner and outer edges. With those values of q, the radii of the ring edges at that time can be obtained from Equation (4.5).

Generally inner/outer caustic edges are born together at some non-zero radius and time after impact, at a cusp singularity in space-time. At the birthpoint we have both r / q = 0 and ²r / q² = 0 (because it is a cusp singularity). An expression for the latter condition can be obtained by differentiating Equation (4.13), yielding

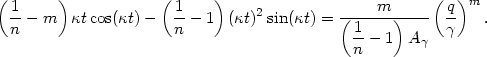
(4.14)

Combining Equations (4.13) and (4.14), we get the birthpoint Equation

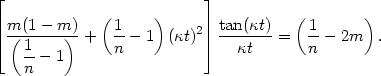
(4.15)

The separability of q and t in Equations (4.13) and (4.14) implies that the explicit dependence on q can be eliminated, as in Equation (4.15). Thus, the latter can be solved for t (in each phase interval of length 2), and then q, t, and r can be derived for the birth of the caustic ring. Equation (4.15) also shows that the birth phase t does not depend on the amplitude A, though it does depend on the variation of amplitude with radius through the parameter m. The birth values of q(r) and t do depend on A.

This completes the analytic caustics model for symmetric (power-law) rings. This model is very simple, involving no more than two derivatives of a sinusoidal function. However, the dependencies on the three parameters m, n and A allows for a wide variety of forms. Examples and limiting cases will be described in the following section. In comparing to observations, e.g., in looking at aging starburst populations behind a ring, the absolute length and time scales, and 2 / are also important.