6.2.2. The Next Generation: 1980s

The next generation of hydrodynamical models were based on a finite difference algorithm, Flux Corrected Transport or FCT (Appleton, Struck-Marcell and Foster 1985; Foster 1985; Appleton and Struck-Marcell 1987b; Struck-Marcell and Appleton 1987). Although smoothed particle hydrodynamics (SPH) methods were beginning to show much promise at this time, finite difference algorithms were the method of choice for modeling shocks, which was one of the primary motivations of these models. Two results emerged from these models, which were at first somewhat surprising. The first was that, at least within the region of parameter space explored with these models, strong shocks did not occur within first rings. However, in second rings, the shocks were very strong. In the light of the KIA models of Section 4 and the discussion of the above, this is understandable. The epicyclic motions of gas elements at adjacent radii do not generally get far out of phase until they have passed through the first ring.

The work of Appleton and Struck-Marcell also included a simple cloud fluid model for the effects of interstellar cloud coalescence, cloud collisional disruption, and young star activity on the local cloud mean mass, and the mean random velocities in the local cloud system (see the review of Struck-Marcell, Scalo and Appleton 1987). These models represented a first attempt to study the effects of ring waves on interstellar cloud structures, and to use the cloud fluid model to investigate the occurrence of wave-driven starbursts, and their nonlinear feedbacks. The primary success of the cloud fluid simulations was that they showed a very nonlinear star formation response in the ring wave in some cases, in accord with the suggestion of Davies and Morton (1982) for the Cartwheel. Specifically, in the one-dimensional models of Struck-Marcell and Appleton (1987), if the ring pushed the gas density well above a critical value, where the model star formation function increased nonlinearly, a strong burst occurred in the wave. However, in collisions with 10% and 20% mass companions, the density enhancement in the first ring was generally not great enough to yield a burst. On the other hand, bursts occurred in the strong second wave in all cases. Moreover, there was a strong suppression of star formation in the rarefaction region between the two waves in all cases. Most ring galaxies have only one visible ring. This result implied that if these starburst rings are the first wave in the target disk, then either the precollision gas density was quite close to the critical value, or the companions tend to be more massive. It now seems likely that the model threshold functions were unrealistically sharp. Since they were not intended to provide a highly realistic representation of the relevant physics, the results should not be over-interpreted. Nonetheless, several systems are known with a weak outer ring, but a much stronger inner ring (e.g., AM 2159-330). The result also highlights the possibility that some observed outer rings, especially in systems without nearby companions, might be second or higher order waves (see discussion on the Cartwheel in Section 6.4).

Another symptom of the nonlinearity of the cloud fluid terms was the generation of secondary bursts by a strong burst in the wave. That is, strong bursts generated pressures high enough to push the gas away to slightly larger and smaller radii, where new bursts occurred. Struck-Marcell and Appleton (1987) showed that subsequently, a rather chaotic pattern of star formation peaks were generated in the propagating wave (see Figures 16, 22 in Struck-Marcell and Appleton 1987). This behavior is a specific instance of the general tendency of the cloud fluid to undergo a bifurcation cascade to chaos as the gas density is increased (Scalo and Struck-Marcell 1986). To date, there is little observational evidence for such pressure feedbacks in ring waves. Higher resolution observations (including Hubble Space Telescope observations) may yet discover multiple star formation peaks at adjacent radii, but it will be hard to determine whether they are the result of this effect, or of star formation occurring in different planes of a warped disk ring.

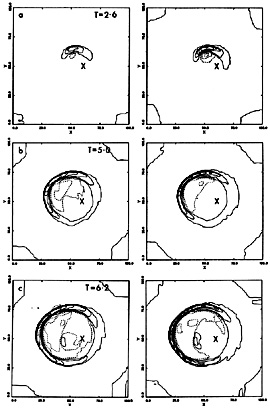
Appleton and Struck-Marcell (1987b) presented two-dimensional models of the primary disk following an off-center collision, with a limited version of the cloud fluid model. In these models the wave begins on the impact side of the disk (somewhat rotated) in a crescent or "banana" shape, extending over a limited range of azimuths (see Figure 19). The wave spreads in azimuth as it propagates outward, not because of shear, but because the perturbation appears more symmetric in the outer disk. Ultimately at large radii compared with the impact radius, the ends of the crescent join to form a complete if asymmetric ring. As discussed above, asymmetric rings are common, and "banana" waves are suggested by the observations (see for example, Appleton, Schombert and Robson 1992). Asymmetric waves are also apparent in earlier restricted three-body and N-body simulations, although they are much more dramatic in the hydrodynamic simulations because of the greater compression. The overall asymmetry is readily understandable as the result of the effect of the different distances between points on a circular annulus in the disk and the impact point on the perturbation amplitude. However, in the collisionless stars a stronger radial perturbation yields a thicker ring (Section 4), with overdensities that are less than those in the collisional gas.

Figure 19. Figure 7 of Appleton and Struck-Marcell (1987b) showing contour maps of gas density (left hand panel) and star formation rate functions (right panel) for an off-center collision simulation. Solid contours indicate elevation above the initial unperturbed values and dotted contours show depressed levels.

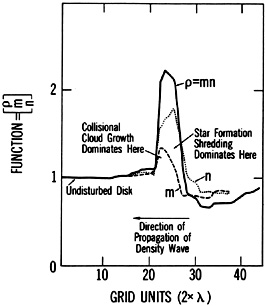
The models of Appleton and Struck-Marcell (1987b) also yielded predictions about the variation of cloud collisional and star formation processes across a ring wave. Specifically, a region of cloud collisional buildup was predicted in the outer parts of a typical wave, followed by star formation and cloud disruption as the gas exits the inner parts of the wave (see Figure 20, from Appleton and Struck-Marcell 1987b). High resolution multiwavelength studies of the spiral arms of M51 (see review of Rand and Tilanus 1990) show evidence of the dissociation of the molecular gas in the vicinity of HII regions downstream of the gas and dust peak in the southern arm (but see also discussion by Casoli (1991) on the more complex situation in the northern wave). A similar phenomenon is observed in M81 (Kaufman et al. 1989) and in the central regions of M33 (Wilson and Scoville 1991; Regan and Wilson 1993), though in both cases the dust or molecular gas doesn't seem to be concentrated in as sharp a front as in M51. It will be more difficult to resolve comparable structures in the more distant ring galaxies. However, in many rings the star formation is more vigorous and violent, so the corresponding effects should be visible on larger scales. This is certainly the case in the Cartwheel, as discussed below.

Figure 20. Figure 4 of Appleton and Struck-Marcell (1987b) showing an enlarged, sectional slice of the variation through a ring wave of the mean cloud mass m, and number density n in the cloud fluid model.