Annu. Rev. Astron. Astrophys. 1988. 26: 509-560 Copyright © 1988 by Annual Reviews. All rights reserved

6.3. A Case for Simplicity

Apart from this last-mentioned suggestion that the brightest galaxies lie preferentially in dense environments (probably as a result either of stochastic sampling or of dynamical evolution), there is no evidence that the shape of the type-specific LFs, _T(M), depends on the local density (see Section 5 and Figure 1). Perhaps the strongest case against a density dependence of _T(M) comes from the Virgo and Coma clusters. Despite the very different type mixtures of these clusters (namely E: S0: S+Irr = 12:26:62% for Virgo, but 44:49:7% for Coma), the LFs of these three bins of galaxies are essentially identical (Binggeli 1987).

Adopting the hypothesis that _T is independent of D, i.e. _T(M, D) = _T(M), one can treat the total (M) as a function of type and density by expanding the formalism in Section 2 (Equations 8-11) as

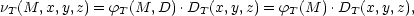
(21)

where

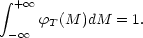
(22)

This means that the separability of and D (Equation 8) is recovered for any given T.

If f_T(D) is the relative frequency of a given type over all magnitudes as a function of the density, one can write

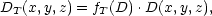
(23)

where

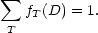
(24)

From Equations 21 and 23, the sum over all types becomes

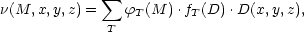
(25)

and the LF over all types is therefore

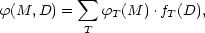
(26)

where (from Equations 22 and 24),

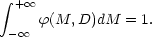
(27)

Equation 26 clearly reflects that the general LF is not universal. Instead, it is the sum over all type-specific LFs weighted by the density-dependent type fraction.

The difficulty with the normalization in Equations 22 and 27 is that the integration of to infinity is impractical because at least the LF of dEs is exponential. A solution to the problem was suggested with Equation 11, where was integrated to a specified absolute magnitude 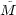. If this procedure is again adopted here, the type fraction f_T(D) also becomes a function of 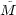. Therefore, as stressed already by de Souza et al. (1985), the same magnitude cutoff 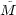must be used for the morphology density relation. Equation 26 can then be reformulated as

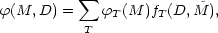
(28)

where

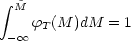
(29)

and

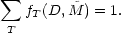
(30)

A remaining question is to what detail the type binning should be carried. The minimum detail required for spirals is the differentiation into subtypes, because the subtypes have different LFs (cf. Figure 1) and follow different morphology-density relations, as discussed in Section 5.3. Therefore, in order that _T be universal, the morphological binning should be at least as fine as that used in Figure 1. But it is not clear whether this degree of differentiation is sufficient. It was conjectured in Section 6.1 that the morphology-density relation may extend down into the finest morphological separation. However, the morphological binning must not reach the point where every galaxy is treated as an individual; otherwise the hypothesis that _T is universal would be trivially true. A fine T-binning is often also impractical e.g. for the LFs of distant clusters. Nevertheless, even with a coarse binning the hypothesis of constant _T may be a valid and useful approximation.

The precise universality of _T is not to be expected for other reasons as well. Dynamical interaction with the intracluster medium and between galaxies in the central parts of clusters has some influence on the evolution (Dressler 1984) and also on (M) (cf. Section 4.1). But, following the introduction of a general LF over all types by Abell (1962, 1964), its consolidation by Schechter (1976), and its canonization by Felten (1977, 1985), the present hypothesis that the type-specific _T(M) is universal, independent of the environment, is probably the next logical step for an understanding of the LFs of galaxies. Of course, its validity must be tested further.