Annu. Rev. Astron. Astrophys. 1984. 22: 157-184 Copyright © 1984 by Annual Reviews. All rights reserved

2.4. The Cosmological Constant

When the cosmological constant is taken into account, the field equations (Equation 7) are altered to

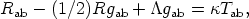
(12)

which can be rewritten in the form

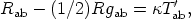
(13a)

where

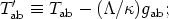
(13b)

that is, the field equations can be regarded as the same as before but with an altered stress-energy tensor. Writing the effective stress-energy tensor T'_ab in the form of Equation 4a, one finds that

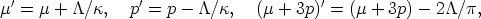
(14a)

and so Equation 10 becomes

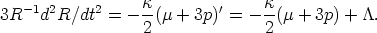
(14b)

If the -term is large enough, the argument by which Equation 10 leads to Equation 11 no longer applies, for the effective active gravitational density (µ + 3p)' can violate the energy condition Equation 9b. If it does so at all times, a singularity in the past can be avoided (cf. Equation 14b), and indeed it has long been known (86) that there are FLRW universes with a large positive cosmological constant that (a) start expanding from a state asymptotically like the Einstein static universe [Eddington (23) suggested that this was preferable to a "big bang" origin]; or (b) collapse from infinity to a minimum radius value R_min > 0 and then reexpand to infinity.

There are two problems with these models. Firstly, the deceleration parameter q₀ - (1 / R)₀(d²R / dt²)₀ / (H₀²) must be negative at all times in these universes (for if it ever becomes positive, the universes must come from a singular origin), but observations suggest that the present value of q₀ is positive (114). Secondly, an alternative explanation for the CMBR must be found in these cases, for it is not possible for this radiation to arise from a hot early stage in such a universe. The reason is that if such a hot early stage were to explain the CMBR, the asymptotic phase or turnaround caused by would have to occur during the early plasma phase before decoupling when T > 3000 K; thus inequality Equation 9b would have to be violated by the effective matter (see Equation 14) for values of R less than (R₀ / 1000). But at that time, (µ + 3p) would be at least 10⁹ times larger than at present, while would have the same value as at present (because it is constant); violation of Equation 9b at that time therefore implies a value of so large that we would undoubtedly have detected it from q₀. It is difficult to find alternative explanations for the CMBR (54). In addition, these models require element abundances to be arbitrarily set by initial conditions in the Universe (for the argument above shows the turnaround would occur long before nucleosynthesis temperatures were achieved). Thus, these models leave so many questions open as to not be presently viable.

One should note here that it follows from Equations 5, 9, and 14b that a static FLRW universe model will necessarily be unstable. [Perturbing R from a static value R_c will lead either to collapse or expansion (23, 25).] This implies that even if we could find some other explanation for redshift (abandoning Equations 1 and 2) we would not expect a FLRW universe to be static unless we abandon either Einstein's field equations or the energy conditions.