10. IMPLICATIONS FOR COSMOLOGY

One of the classical tests of cosmology is the comparison of timescales. With a knowledge of H₀ , the average density of matter, , and the value of the cosmological constant, , integration of the Friedmann equation

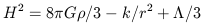
(7)

yields a measure of the expansion age of the universe. This expansion age can be compared with other independent estimates of the age of the Galaxy and its oldest stars, t₀, and thus offers a test of various possible cosmological models. For example, the dimensionless product, H₀ t₀, is 2/3 in the simplest case where _m = 1, = 0 (the Einstein-de Sitter model), and the product is 1 for the case of an empty universe where the matter and energy density are zero.

An accurate determination of the expansion age requires not only the value of H₀ , but also accurate measurements of _m and . At the time when the Key Project was begun, the strong motivation from inflationary theory for a flat universe, coupled with a strong theoretical preference for = 0, favored the Einstein-de Sitter model (e.g., Kolb & Turner 1990). In addition, the ages of globular cluster stars were estimated at that time to be ~ 15 Gyr (VandenBerg, Bolte & Stetson 1996; Chaboyer et al. 1996). However, for a value of H₀ = 72 km s^-1 Mpc^-1, as found in this paper, the Einstein-de Sitter model yields a very young expansion age of only 9 ± 1 Gyr, significantly younger than the globular cluster and other age estimates.

Over the past several years, much progress has been made toward measuring cosmological parameters, and the Einstein-de Sitter model is not currently favored. For example, estimates of cluster velocity dispersions, X-ray masses, baryon fractions, and weak lensing studies all have provided increasingly strong evidence for a low-matter-density (_m) universe (e.g., Bahcall & Fan 1998). In addition, strong new evidence for a flat universe has emerged from measurements of the position of the first acoustic peak in recent cosmic microwave background anisotropy experiments (de Bernardis et al. 2000; Lange et al. 2000). Together with evidence for a low matter density, and with recent data from high-redshift supernovae (Riess et al. 1998; Perlmutter et al. 1999), evidence for a non-zero cosmological constant has been increasing. Moreover, the age estimates for globular clusters have been revised downward to 12-13 Gyr, based on a new calibration from the Hipparcos satellite (Chaboyer 1998; Carretta et al. 2000). A non-zero value of the cosmological constant helps to avoid a discrepancy between the expansion age and other age estimates. For H₀ = 72 km s^-1 Mpc^-1, _m = 0.3, = 0.7, the expansion age is 13 ± 1 Gyr, consistent to within the uncertainties, with recent globular cluster ages. In Table 15, we show expansion ages for different values of H₀ and a range of flat models.

Table 15. Expansion Ages (in Gyr) for Flat Universes ^a

In Figure 9 H₀t₀ is plotted as a function of . Two curves are shown: the solid curve is for the case where = 0, and the dashed curve allows for non-zero under the assumption of a flat universe. The ± 1- and 2- limits are plotted for H₀ = 72 km s^-1 Mpc^-1, t₀ = 12.5 Gyr, assuming independent uncertainties of ±10% in each quantity, and adding the uncertainties in quadrature. These data are consistent with either a low-density (_m ~ 0.1) open universe, or a flat universe with _m ~ 0.35, = 0.65; however, with these data alone, it is not possible to discriminate between an open or flat universe. As described above, recent studies favor _total = 1, a low-matter-density universe (_m ~ 0.3), and a non-zero value of the cosmological constant. Note, however, that the open circle at _m = 1, = 0, represents the Einstein-de Sitter case, and is inconsistent with the current values of H₀ and t₀ only at a ~ 2- level.

Figure 9. H0t0 versus for H0 = 72 km s-1 Mpc-1, t0 = 12.5 Gyr, and uncertainties of ± 10% adopted for both quantities. The dark line indicates the case of a flat Universe with + m = 1. The abscissa in this case corresponds to . The lighter curve represents a Universe with = 0. In this case, the abcissa should be read as m. The dashed and dot-dashed lines indicate 1- and 2- limits, respectively for values of H0 = 72 and t0 = 12.5 Gyr in the case where both quantities are assumed to be known to ±10% (1-). The large open circle denotes values of H0t0 = 2/3 and m = 1 ( i.e., those predicted by the Einstein-de Sitter model). On the basis of a timescale comparison alone, it is not possible to discriminate between models with m ~ 0.1, = 0 or m ~ 0.35, ~ 0.65.