5.1. Low Lying States for Particles in Uniform Magnetic Fields

Following Refs. [216, 217] in this section we will consider questions related to the mass shifts and decay of bound states of quarks. Mass shifts occur both due to the effect that magnetic fields have on the strong binding forces, and due to the direct interactions of charged spinning particles with external fields. The modifications of the strong forces are such as to close the gap between the proton and neutron masses and ultimately make the proton heavier. A delicate interplay between the anomalous magnetic moments of the proton and neutron drives the mass shifts due to the direct interactions in the same direction. For B > 1.5 × 10¹⁸ G the neutron becomes stable and as the field is increased past 2.7 × 10¹⁸ G the proton becomes unstable to decay into a neutron, positron and neutrino.

The quantum mechanics of a Dirac particle with no anomalous magnetic moment in a uniform external magnetic field is straightforward. We shall present the results for the case where particles do have such anomalous moments. In reality, in fields so strong that the mass shifts induced by such fields are of the order of the mass itself one cannot define a magnetic moment as the energies are no longer linear in the external field. Schwinger [37] calculated the self energy of an electron in an external field and we shall use here his results. We cannot follow this procedure for the proton or neutron as we do not have a good field theory calculation of the magnetic moments of these particles, even for small magnetic fields; all we have at hand is a phenomenological anomalous magnetic moment. However, for fields that change the energies of these particles by only a few percent, we will consider these as point particles with the given anomalous moments. In the Sec. 5.1.7 we will discuss possible limitations of this approach.

5.1.1 Protons in an External Field

The Dirac Hamiltonian for a proton with a uniform external magnetic field B is

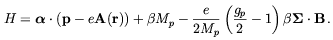
(5.1)

The vector potential A(r) is related to the magnetic field by A(r) = 1/2 r × B and g_p = 5.58 is the proton's Landé g factor. We first solve this equation for the case where the momentum along the magnetic field direction is zero and then boost along that direction till we obtain the desired momentum. For B along the z direction and p_z = 0 the energy levels are [38]

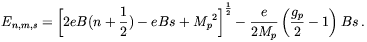
(5.2)

In the above, n denotes the Landau level, m the orbital angular momentum about the magnetic field direction and s = ± 1 indicates whether the spin is along or opposed to that direction; the levels are degenerate in m. n = 0 and s = +1 yield the lowest energy

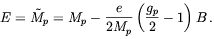
(5.3)

As we shall be interested in these states only we will drop the n and s quantum numbers. The Dirac wave function for this state is

(5.4)

_m's are the standard wave functions of the lowest Landau level:

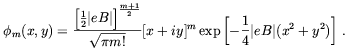
(5.5)

Boosting to a finite value of p_z is straightforward; we obtain

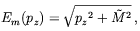
(5.6)

with a wave function

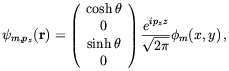
(5.7)

where 2, the rapidity, is obtained from tanh 2 = p_z / E_m(p_z).

In the non-relativistic limit the energy becomes

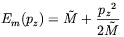
(5.8)

and the wave function reduces to

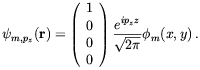
(5.9)