

In this section, I shall give a brief overview of the properties of the Universe at large. On the largest scales it can be reasonably approximated as a homogeneous and isotropic medium in a state of uniform expansion and the equations can easily be written down. We find that such a simple model Universe can be described in terms of a few parameters, the expansion rate, the density, and perhaps the cosmological constant. Classical cosmology focusses on determining these by direct observation of the large scale distribution of galaxies. There are, however, many new techniques available for getting these parameters though studying the inhomogeneity of the Universe. These will be the subject of the following sections where many of the issues raised here will be discussed at greater length.
Hubble discovered the expansion of the Universe by plotting, for a sample of galaxies, the radial velocity of each galaxy as indicated by the redshift of its spectral lines against its apparent brightness. The fainter (and presumably more distant) galaxies had the greater recession velocities (or "redshifts"). If the distance to a galaxy was D Megaparsecs, and its radial velocity was V km s-1, then Hubble's relationship could be expressed as
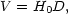
| (1) |
where H0 is a constant (the Hubble constant) measured here in units of km s-1 Mpc-1 Implicit in the relationship is the assumption that we can calibrate the distance scale by virtue of which the apparent brightness of a galaxy can be turned into a distance.
The radial component of the velocity of a galaxy relative to the
observer is inferred by observing the wavelength
 0 of spectral
lines that would in the laboratory have been emitted wavelength
0 of spectral
lines that would in the laboratory have been emitted wavelength
 E. The
difference
E. The
difference 
 =
=
 0 -
0 -
 E is
interpreted as being due to the Doppler
shift caused by the fact that the galaxy was moving at velocity
E is
interpreted as being due to the Doppler
shift caused by the fact that the galaxy was moving at velocity
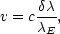
| (2) |
relative to the observer. (We shall henceforth drop the `E' suffix on the emitted wavelength). The redshift of the galaxy (in fact the redshift of the spectra lines) is defined as
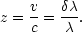
| (3) |
Hubble's redshift-distance relation (the "Hubble Law") later became a way of estimating the distances to galaxies simply by measuring their radial velocities Dz = H0-1 cz. (Dz has the subscript z to denote the nature of this distance estimate and to distinguish it from the true distance. We shall see later that part of the velocity cz may be due to the random motions of galaxies relative to the general cosmic expansion.)
Looked at in its most simple terms, Hubble's discovery implies that the Universe was born a finite time in our past and emerged from a state of infinite density. The subsequent discovery by Penzias and Wilson (1965) of a cosmic microwave background radiation field and its interpretation as the relict of an expansion from a hot singular state by Dicke, Peebles, Roll and Wilkinson (1965) established a definitive view of our Universe. Cosmology properly became a branch of physics, and the Hot Big Bang theory has become a paradigm of modern science.
1.1.1. Homogeneity and Isotropy
On the smallest scales the Universe contains stars that are grouped into galaxies, that are themselves grouped into clusters. Going to larger scales we have evidence for clusters of galaxy clusters, and beyond that for large scale structures ("walls" of galaxies!) extending over many tens or even hundreds of megaparsecs. Indeed pictures of the three dimensional distribution of galaxies look very inhomogeneous even on scales as large as 100 Mpc, or more. However, one should not be mislead by visual appearances. As will be explained later, this large scale inhomogeneity has rather a small amplitude in the sense that it would hardly be noticeable if the distribution of galaxies were smoothed over such large volumes. There is a clear tendency for the Universe to become more homogeneous on ever large scales.
Hubble himself commented on the remarkable large-scale isotropy of the Universe as judged from the distribution of galaxies on the sky. Today we have catalogues of galaxies penetrating to great distances (Maddox et al., 1990) and these demonstrate the isotropy of the galaxy distribution very clearly. The isotropy of the Universe is best measured through the isotropy of the cosmic microwave background radiation.
The large scale homogeneity of the Universe is more difficult to establish directly. It would seem reasonable to use the argument that we are not at the center of the Universe, so the isotropy must imply spatial homogeneity, but this is not a proof of homogeneity. The same deep galaxy catalogues provide a test of homogeneity because we can ask the question "is the Universe, sampled at various depths within this catalogue, the same?". Again the Maddox et al. (1990) catalogue provides an answer, though the method is not as simple as observing isotropy. Maddox et al. compute the galaxy clustering correlation function at various depths in their catalogue and find that the functions in the various samples scale in accordance with the hypothesis of homogeneity. Their analysis in fact goes even further than merely saying that the Universe is globally homogeneous. It has the additional implication that the deviation from homogeneity (as evidenced by the galaxy clustering) is itself the same in all their samples.
Such arguments provide compelling evidence that the Universe is not a hierarchy of the kind originally envisaged by Charlier (1908, 1922), and taken up more recently in the context of fractal distributions of galaxies by Mandelbrot (1983), Coleman, Pietronero and Sanders (1988) and others.
1.1.2. Scale Factors, Redshifts and all that
For most of what concerns us in these lectures it is sufficient to consider the Universe to be, in a first approximation, a homogeneous and isotropic distribution of particles (galaxies) that interact only through their mutual gravitational interactions. This means that we ignore any pressure contribution from their random motions, or from other components of matter. This enables us to greatly simplify the dynamical equations for the evolution of the Universe.
Consider the motion of a galaxy in the Universe that today (t0) is at distance l0 from us and that at time t was at a distance l (t). It is convenient to define the scale factor a(t) by
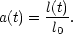
| (4) |
Since the Universe is presumed homogeneous and isotropic, then a(t) depends on neither position nor direction. It merely describes how relative the distances change as the Universe expands. We have normalized all lengths relative to their present day value and so the present value of a(t) is a(t0) = 1.
The Einstein equations (or their Newtonian equivalent) in the simple
case of homogeneous and isotropic dust models give the differential
equation for the scale factor in terms of the total mass density
 :
:
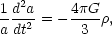
| (5) |
This is supplemented by an equation expressing the conservation of matter:
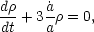
| (6) |
which is equivalent to
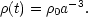
| (7) |
Note that (5) is not valid if there is any substantial pressure due to the matter in the universe, and in that case we also need to modify (6). We shall make these modifications at a later time when needed, for the moment we are only discussing the Universe at the present time and in its recent past when equations (5, 6, 7) are thought to be a good approximation.
The Hubble Parameter is defined as
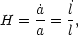
| (8) |
and is a function of time. H describes the rate of expansion of the
Universe and has units of inverse time. It is experimentally measured
as a velocity increment per unit distance since it describes the
expansion through the relationship between velocity and distance:
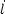 = H l, or in more
familiar notation v = H r.
= H l, or in more
familiar notation v = H r.
We define the redshift to a galaxy at distance l to be
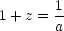
| (9) |
When we look at a distant galaxy we are looking at it as it was in the past (because of the finite light travel time). At the time we are seeing it, the scale factor a(t) was smaller than the present value (a0 = 1). It can easily be shown that the recession velocity we measure from the shift in the spectral lines is just cz, in other words, the quantities z appearing in equations (3) and (9) are the same thing.
1.1.3. Important quantities: H0,
 0,
0,
 c
c
At this point it is convenient to introduce some fundamental
definitions. Hubble's expansion law states that the recession velocity
of a galaxy is proportional to its distance from the observer, in
other words 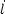
 l0. The constant of proportionality (the
cosmic expansion rate) is the present value of the Hubble parameter:
l0. The constant of proportionality (the
cosmic expansion rate) is the present value of the Hubble parameter:
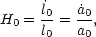
| (10) |
H0, the present value of the Hubble Parameter, is usually called "Hubble's Constant".
There is an important value of the density,
 c,
that can be derived
from the Hubble parameter (the Hubble parameter has dimensions
[time]-1). This is the density such that a uniform
self-gravitating sphere of density
c,
that can be derived
from the Hubble parameter (the Hubble parameter has dimensions
[time]-1). This is the density such that a uniform
self-gravitating sphere of density
 c
isotropically expanding at rate H has equal
kinetic and gravitational potential energies:
c
isotropically expanding at rate H has equal
kinetic and gravitational potential energies:
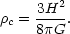
| (11) |
Since H is a function of time, then so is
 c.
c.
We can measure the density of the Universe in terms of
 c by
introducing the density parameter
c by
introducing the density parameter
 :
:
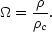
| (12) |
Note that  also
depends on time and we shall denote the present day
value of
also
depends on time and we shall denote the present day
value of  by
by
 0. There
may be a mixture of different type of matter
in the universe that make up the total density
0. There
may be a mixture of different type of matter
in the universe that make up the total density
 . We may think, for
example, of baryons, photons and perhaps some exotic elementary
particles. Each of these individually has a density that can be
normalized relative to
. We may think, for
example, of baryons, photons and perhaps some exotic elementary
particles. Each of these individually has a density that can be
normalized relative to
 c,
thus each species has its own
c,
thus each species has its own
 . We will, for
example, denote the contribution of Baryonic
material to the total cosmic density by
. We will, for
example, denote the contribution of Baryonic
material to the total cosmic density by
 B.
B.
The density
 c
has a special significance. A universe whose density
is
c
has a special significance. A universe whose density
is  c
when its expansion rate is H is referred to as an Einstein de
Sitter universe. This model clearly has
c
when its expansion rate is H is referred to as an Einstein de
Sitter universe. This model clearly has
 = 1 at all
times. The expansion rate of such a universe is fixed by the density. Model
universes that are denser than
= 1 at all
times. The expansion rate of such a universe is fixed by the density. Model
universes that are denser than
 c
= 3H2 / 8
c
= 3H2 / 8 G when their expansion rate
is H will stop expanding and contract down to future
singularity. Models that are less dense will expand forever. The
G when their expansion rate
is H will stop expanding and contract down to future
singularity. Models that are less dense will expand forever. The
 = 1
universe is a limiting case dividing two classes of behaviour and that
is why the parametrization of the density in terms of
= 1
universe is a limiting case dividing two classes of behaviour and that
is why the parametrization of the density in terms of
 c is so
useful. The behaviour of the various model universes as a function of
c is so
useful. The behaviour of the various model universes as a function of
 can be seen by
looking at dynamical equation for the expansion factor a(t).
can be seen by
looking at dynamical equation for the expansion factor a(t).
Equations (5) and (7) for a(t) can be shown to integrate to
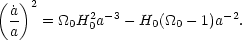
| (13) |
The integration constants have been derived using the boundary
condition that a(t)
 0 as
t
0 as
t  0,
(
0,
( / a)0
= H0 and that the present density of matter is
/ a)0
= H0 and that the present density of matter is
 0 =
0 =
 0
0
 c.
The standard textbooks referred to
above give the solutions of this equation for general values of
c.
The standard textbooks referred to
above give the solutions of this equation for general values of
 0. It
is sufficient here to note that the case
0. It
is sufficient here to note that the case
 0 = 1
simplifies the right hand side of this equation and the solution is then
particularly simple
0 = 1
simplifies the right hand side of this equation and the solution is then
particularly simple

|
Since a(t) = (1 + z)-1 this tells us that when we look back to a redshift z in Einstein de Sitter universe we are seeing the universe when its age is a fraction t / t0 = (1 + z)-3/2 of its present age, t0.