4.2. Modelling the Evolution of Large Scale Structure

4.2.1. CDM models

The most extensively studied spectrum of primordial density fluctuations is the one arising from the "Cold Dark Matter" theory in which the mass density of the universe is made up to = 1 by massive weakly interacting particles such as axions. The spectrum at recombination is entirely determined by the initial spectrum (generally taken to be Harrison-Zeldovich) and the physical processes that occur in the pre-recombination fireball. The bulk of the work on this model has been done numerically and is described in a series of papers by Davis, Efstathiou, Frenk and White (Efstathiou et al., 1985; Davis et al., 1985; White et al., 1987; Davis and Efstathiou, 1988).

Apart from the initial amplitude of the spectrum, which determines the epoch of galaxy formation, the theory is entirely fixed and has no free parameters as far as the dynamics is concerned. However, when it comes to relating mass and light distributions it is found necessary to introduce a bias parameter, b, defined in terms of the density contrasts of the distribution of matter and luminosity by

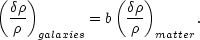
b enters into the normalization of the model. This universe has ₀ = 1 and models are normalized so that the rms light fluctuation in a sphere of radius 800 km s^-1 is unity. Hence the normalization of the mass fluctuations in 800 km s^-1 spheres is just b^-1.

(This normalization is not the only possibility. It is possible to choose the scale where the two-point correlation function drops to unity to be 5h^-1 Mpc, or to normalize through the function J₃(r) = r² (r) dr whose (somewhat uncertain) value is estimated to be J₃(10h^-1 Mpc) = 277h^-3 Mpc³ and J₃(30h^-1 Mpc) 800h^-1 Mpc³ (Davis and Peebles, 1983).)

There have been many theoretical discussions of the value of b (see Dekel and Rees, 1987, for a review), but there are no reliable methods of estimating what its value should be. At present b has to be inferred from the observations. Braun, Dekel and Shapiro (1988) looked into various biasing mechanisms and showed that it is possible to get galaxy formation to start at z ~ 3 and have a galaxy-galaxy correlation function with the correct slope today. (Though there was then a problem with the correlation length scale).

The value b = 2.5 is motivated by the N-body models Davis et al. (1985). However, b = 2.5 appears to be inconsistent with the observed streaming motions (Bertschinger and Juskiewicz, 1988; Górski, 1988). Kaiser (1988), for example, prefers b = 1.5. Peebles, Daly and Juskiewicz (1989) review this question in detail, looking at the consequences of various choices for b and for the lengthscale for mass clustering, r₀. They argue, for example, that b = 1.5 is too low to be consistent with the pairwise galaxy velocity correlation if b = 1.5 and r₀ = 7h^-1 Mpc. Lowering r₀ to 4 h^-1 Mpc creates problems with cluster velocity dispersions (Evrard, 1989).

One way around these problems may be to introduce non-Gaussian initial conditions. Several numerical simulations have been done on these lines by Messina et al. (1990), using negative binomial and lognormal distributions.

The extra degree of freedom provided by the skewness of the initial distribution is of course beneficial and in particular the structures that are formed are well organised into filamentary structures. These simulations look highly promising.

So is the standard CDM model dead? It certainly has problems but source of the problems is easy to identify: the rather naive notion of biasing. It is conceivable that a better model of galaxy formation which automatically dealt with the biasing that has been put in to model the luminosity formation process could be made to work. The bias parameter was introduced to solve a problem: the amplitude of the velocities on the small scales were too great if the normalization was performed on the assumption that the mass and light distributions are identical (b = 1). Increasing the large scale amplitude in order to solve the problems that appear on large scales therefore has bad effects on the smaller scales. The small scale correlation function amplitude becomes too great and the velocity dispersion increases. That conclusion is however predicated on the assumption that CDM describes the small scale evolution correctly. Other effects, like dynamical friction and mergers in systems of galaxies that are not accurately modelled in the simulations could be taking place. So we must await even bigger (N > 10⁶ or 10⁷ -body models).

4.2.2. CDM with "gas"

There have been a number of attempts to take CDM further and consider gas flows in the potentials created by the dark matter (Carlberg and Couchman, 1989). Three dimensional simulations lack resolution and so Klypin et al. (1990) have done a high resolution CDM simulation in 2 dimensions, using a cloud-in-cell method to solve the equations of motion of the dark matter. The baryonic component is supposed to be glued to the dark matter, and its thermal history is computed along particle trajectories. In a 50 Mpc. box, the resolution is 50-100 kpc. That is the advantage of working in two dimensions. The simulations show remarkable large scale filaments and voids, reminiscent of the de Lapparent et al. (1986) picture. This conclusion is supported by the adhesion model simulations of CDM (Weinberg and Gunn, 1990).

The Klypin et al. simulations show a remarkable feature: the overall structure of the model is not dominated by the smallest scales in the simulation. The galaxies lie along large scale filamentary structures (though because of the two dimensional nature of the simulation, we cannot say whether these features would be filament like or sheet like in three dimensions). This effect is apparently due to the effect of the velocity field correlations (Klypin, private communication). It will be interesting to see if this conclusion is borne out by very large three dimensional simulations.

4.2.3. Adhesion Model

The "pancake" theories for galaxy formation are well described by an elegant analytic approximation to the evolution of cosmic structure first proposed by Zeldovich (1970). In that approximation the position x_i of a particle in comoving coordinates is given relative to its position q_i at some starting time t₀ by the expression:

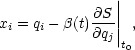
(62)

where S(q_i, t₀) is the velocity potential field at the time t₀. The form of the function (t) depends on the cosmological model, but in the case = 1 it is simply (t) = (t/t₀)^2/3.

The peculiar velocity of a particle initially at point q is given in terms of S by

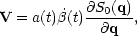
(63)

and S is directly related to the density fluctuation amplitude at time t₀:

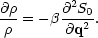
(64)

From the equation we see that the approximation is essentially a ballistic approximation in comoving coordinates with respect to the cosmic -time. The gravitational effects of the surrounding mass distribution is not taken into account except insofar as gravity was responsible for causing the conditions at t₀. The approximation agrees with linear theory for the growth of small amplitude density contrasts. An improvement on this simple form of the approximation has been given by Buchert (1989).

The major problem with the Zeldovich solution is the fact that when the particle orbits intersect, a shock wave should form, dissipating the kinetic energy of the colliding streams (and forming the "pancakes" which fragment to make the galaxies). The dissipation is not a part of the approximation and so the streams penetrate and the pancakes get thicker after a time. Gurbatov et al. (1985, 1989) found a way of including dissipation in the Zeldovich approximation and at the same time reducing it to a set of equations well known in the one dimensional case as "Burgers" equation. If we write the Zeldovich approximation as a fluid flow, then the equation of motion is

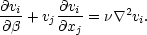
(65)

The ² v_i "viscosity" term is introduced to prevent orbit crossing. Note that the `time' is -time.

Several things should be noted about this equation. Firstly, there are no forces on the right hand side due to either pressure or gravity. This reflects the way in which the Zeldovich approximation is a ballistic approximation. Secondly, there is no explicit appearance of the density as would have been expected if were a real viscosity. This has an important consequence: the equation conserves velocity rather than momentum in the comoving system. This may cause systematic deviations between the adhesion approximation and N-body simulations that start from the same initial conditions. Thirdly, the equation has an analytic solution. If an explicit density dependence were introduced, there would be no analytic solution and the method would have little to commend it.

The equation has an analytic solution (given in terms of a rather uninformative Green's function). Numerical simulations in two dimensions using the Burgers approximation are relatively straightforward to implement, but there are some problems in three dimensions (Nusser and Dekel, 1990). An alternative scheme avoiding such problems (and directly incorporating biasing) have been developed by Appel and Jones (in preparation).

The "adhesion model" avoids the crossing streams problem and provides the possibility of making analytic studies of cosmological models with arbitrary spectra of inhomogeneities. The approximation is still limited in that it is purely kinematic, the force of gravity plays no part in the evolution of the density field. It is also formally valid only as long as the density contrast is not too high. This last problem was handled by Kofman, Pogosyan and Shandarin (1989) by using a second order modification of the Zeldovich approximation (there is great scope for work in that direction). So the major problem remains the fact that the orbits of the particles are not gravitationally deflected. This has consequences as can be seen in the comparisons (Kofman et al., 1989; Weinberg and Gunn, 1990) that have been made between the adhesion approximation and N-body calculations: the structural features are all there, but they are frequently in the wrong place.

The adhesion approximation has been used by Weinberg and Gunn (1990) to simulate galaxy redshift surveys to a magnitude limit of 15.5, starting from a CDM spectrum and using a bias parameter b = 2. The results show remarkable large scale structures. (Though, because of the way the adhesion approximation works, there are no "fingers of God" in the pictures). Park's (1990) very large N- body simulations with the same bias parameter confirm this. Park does express a preference for low ₀ on the basis of the appearance of the simulation.

4.2.4. Classical Pancakes

The pancake theory is the archetype theory in which the galaxies form after the large scale structure has been created. The theory had the merit that it was relatively straightforward to do simple numerical simulations based on the Zeldovich's approximation to the evolution of small amplitude density perturbations. Pictures of large scale structure could easily be evolved, and, as it turned out five years later, these bore a striking resemblance to the pictures published by de Lapparent et al. (1986). The basic review of the pancake theory is that of Shandarin and Zeldovich (1989).

The pancake theory is based on a spectrum of primordial density fluctuations that has no high frequencies. The spectral cutoff is supposed to be on scales larger than clusters of galaxies, and so the first thing to form is the large scale structure. In a purely baryonic cosmology with ₀ = 0.1 - 0.2 there is a natural cutoff on such scales provided by the damping mechanisms that operate prior to the recombination epoch. However, it turns out that such large amplitudes are required (because ₀ is low) that the theory violates the limits on the isotropy of the microwave background radiation.

The amplitude problem might be solved by adding dark matter, but it must be a light particle in order that the cutoff scale be large. For a period of time there was a degree of enthusiasm about the possibility the neutrino had a mass of several eV's, and that would have served well to achieve ₀ = 1 while at the same time giving a large characteristic mass. Simulations of the neutrino based theory (Klypin and Shandarin, 1983; Centrella and Melotte, 1984; Centrella et al., 1988) gave clear indications of how the large scale structure might arise.

There are several reasons for the loss of general support for this theory, not the least of which is the fact that the most likely dark matter candidate needed by the theory has been almost, but not quite, ruled out (Scherrer, Melott and Bertschinger, 1989). There may still be problems with the microwavebackground, and there may be serious problems with the fact that galaxies should generally form rather late in this theory.

4.2.5. Decaying WIMPS

One method of saving the pancake theory may lie in supposing that ₀ = 1 is made up of decaying weakly interacting massive particles (`WIMPS'). Doroshkevich has been an advocate of model universes pervaded by unstable dark matter (a heavy neutrino), so that _tot = 1 and _B = 0.1. Numerical simulations by Doroshkevich, Klypin, and Khlopov (1988, 1989) show that galaxies still form in the shocked pancakes, but at much earlier times than in the standard heavy-neutrino theory. (The epoch of formation depends on lifetime of decaying particle).

Decay of matter slows the growth of perturbations, but the decay occurs just before start of nonlinear stage of perturbation growth. (Otherwise the theory encounters a number of difficulties (Efstathiou, 1985; Flores et al., 1986; Vittorio and Silk, 1985)). The amplitudes required appear to cause no problems for the microwave background anisotropy limits.