


2.2. Geometry
It has remained a dream of observational cosmologists to be able to directly measure the geometry of space-time rather than infer the curvature of the universe by comparing the expansion rate to the mean mass density. While several such tests, based on measuring galaxy counts as a function of redshift, or the variation of angular diameter distance with redshift, have been attempted in the past, these have all been stymied by the achilles heel of many observational measurements in cosmology, evolutionary effects.
Recently, however, measurements of the cosmic microwave background have
finally brought us to the threshold of a direct measurement of geometry,
independent of traditional astrophysical uncertainties. The idea behind
this measurement is, in principle, quite simple. The CMB originates from
a spherical shell located at the surface of last scattering (SLS), at a
redshift of roughly
z  1000):
1000):
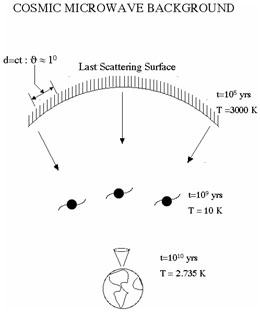
|
Figure 1. A schematic diagram of the surface of last scattering, showing the distance traversed by CMB radiation. |
If a fiducial length could unambigously be distinguished on this surface, then a determination of the angular size associated with this length would allow a determination of the intervening geometry:
Fortunately, nature has provided such a fiducial length, which corresponds roughly to the horizon size at the time the surface of last scattering existed. The reason for this is also straightforward. This is the largest scale over which causal effects at the time of the creation of the surface of last scattering could have left an imprint. Density fluctuations on such scales would result in acoustic oscillations of the matter-radiation fluid, and the doppler motion of electrons moving along with this fluid which scatter on photons emerging from the SLS produces a characteristic peak in the power spectrum of fluctuations of the CMBR at a wavenumber corresponding to the angular scale spanned by this physical scale. These fluctuations should also be visually distinguishable in an image map of the CMB, provided a resolution on degree scales is possible.
Recently, two different ground-based balloon experiments, one launched in Texas and one launched in Antarctica have resulted in maps with the required resolution [7, 8]. Shown below is a comparison of the actual boomerang map with several simulations based on a gaussian random spectrum of density fluctuations in a cold-dark matter universe, for open, closed, and flat cosmologies. Even at this qualitative level, it is clear that a flat universe provides better agreement to between the simulations and the data than either an open or closed universe.
On a more quantitative level, one can compare the inferred power spectra with predicted spectra [9]. Such comparisions, for both the Boomerang and Maxima results yields a constraint on the density parameter:
 = 1.1 ±
.12(95%CL) = 1.1 ±
.12(95%CL)
| (2) |
For the first time, it appears that the longstanding prejudice of theorists, namely that we live in a flat universe, may have been vindicated by observation! However, theorists can not be too self-satisfied by this result, because the source of this energy density appears to be completely unexpected, and largely inexplicable at the present time, as we will shortly see.