Copyright © 1978 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1978. 16:
103-39 Copyright © 1978 by Annual Reviews. All rights reserved |
As has been mentioned above, the velocity fields determined from optical emission lines and from radio-HI data are almost always dominated by the pattern indicative of circular rotation. This applies, of course, to the gas; before going on to discuss these results further in terms of the dynamical properties of galaxies we briefly examine the evidence that the motions of the stars are also represented by the same general kinematics. Of course the information on the rotation of the stars derived from optical absorption lines is mostly restricted to the central regions. The existence of rotational motions near the nucleus of M31 has been known for a long time from the work of Babcock (1939). From rather more extensive observations Rubin et al. (1973) contended that in the central region of M31 the stars exhibit a velocity field as complex as that of the gas; however, Pellet (1976) observed that the stars follow a pattern of symmetric rotation. Recent observations extending further out into the disks of several other galaxies provide a less controversial picture: In NGC 4594 (Faber et al. 1977, Schweizer 1978) the rotation curves of the stars and the gas are very similar. Peterson et al. (1976) show that the rotation of the stars in the bar of NGC 3351 is consistent with that of the gas in the arms emerging at the ends of the bar. Besides the general rotation, local noncircular motions in the stars have been reported in M51, NGC 5866, and NGC 2903 by Simkin (1970, 1972, 1974, 1975a), but these always seem to be associated with dust patches and other details of the spiral structure; these results probably refer to recently formed stars, since Balmer absorption lines are prominent. We can conclude that as yet there is no strong evidence for a major difference in the large-scale kinematics of the gas from that of the stars.
The assumptions necessary to derive a rotation curve
Vrot(R) from
the observed velocity field are: 1. the measurements refer to
positions on a single inclined plane; and 2. rotation is dominant and
all noncircular motions are not part of a large-scale pattern. The
procedure is usually to use least-squares numerical schemes (e.g.
Warner et al. 1973,
van der Kruit 1976a)
to determine five parameters:
position of the rotation center (two numbers), systemic velocity
Vsys,
inclination i of the normal to the galaxy plane with the line of
sight, and the position angle
 0 of the line of
nodes (major axis).
These parameters are determined from different symmetry properties of
the radial velocity field. The influence of small errors in the
parameters is to produce patterns with characteristic symmetries in
the diagram of the radial velocity field after subtraction of the
nominal rotation curve, was first illustrated by
Warner et al. (1973)
and is summarized in Figure 1. In particular a
systematic pattern of
radial expansion or contraction has an effect similar to a change in
0 of the line of
nodes (major axis).
These parameters are determined from different symmetry properties of
the radial velocity field. The influence of small errors in the
parameters is to produce patterns with characteristic symmetries in
the diagram of the radial velocity field after subtraction of the
nominal rotation curve, was first illustrated by
Warner et al. (1973)
and is summarized in Figure 1. In particular a
systematic pattern of
radial expansion or contraction has an effect similar to a change in
 0. Furthermore,
deviations in the velocities owing, for example, to a
density wave may also perturb the derived rotation curve; a detailed
self-consistent model has been used to extract an estimate of the
unperturbed rotation curve of M81 by
Visser (1978a,
b).
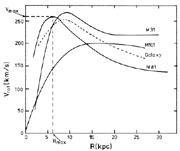
He finds that the value of
Vmax changes by less than a few km/sec, but
Rmax decreases from 6 kpc
(Rots 1975;
see also Figure 2) to 4.8
kpc. Finally, a transverse motion of the galaxy perpendicular to the
line of sight produces errors both in
0. Furthermore,
deviations in the velocities owing, for example, to a
density wave may also perturb the derived rotation curve; a detailed
self-consistent model has been used to extract an estimate of the
unperturbed rotation curve of M81 by
Visser (1978a,
b).
He finds that the value of
Vmax changes by less than a few km/sec, but
Rmax decreases from 6 kpc
(Rots 1975;
see also Figure 2) to 4.8
kpc. Finally, a transverse motion of the galaxy perpendicular to the
line of sight produces errors both in
 0 and in
Vrot(R), but these effects are likely to be small
(Warner et al. 1973).
0 and in
Vrot(R), but these effects are likely to be small
(Warner et al. 1973).

|
Figure 1. Schematic representation of the rotation of disk galaxies and the determination of dynamical parameters. A galaxy with the orientation at top-left shows a pattern of line-of-sight velocities at top-right where lines of equal radial velocity are sketched. The contours close around the radius of maximum rotation velocity on the line of nodes. The conversion from observed to intrinsic parameters is given, as is the systematic pattern of residual velocities when all but one of the dynamical parameters are chosen correctly. This representation was first published by Warner et al. (1973). Note that the patterns are different so that these parameters can be fitted independently to the observed velocity field. The last two examples show the effects of noncircular motions in the radial and tangential direction. |
At the end of the numerical procedure the "best fit" rotation curve
is available. Various refinements have been used, such as determining
i and  0 as
a function of distance from the center by analyzing the
velocity a field in annular rings, determining the rotation curve
separately for the two halves of the galaxy on either side of the
minor axis, etc (e.g.
Rogstad et al. 1974).
0 as
a function of distance from the center by analyzing the
velocity a field in annular rings, determining the rotation curve
separately for the two halves of the galaxy on either side of the
minor axis, etc (e.g.
Rogstad et al. 1974).
|
Figure 2. The rotation curves of M31, M101, and M81 according to Roberts & Rots (1973) are shown as solid lines with that for our Galaxy indicated with the dashed line. The parameters Rmax and Vmax are indicated for the case of M81 (adapted from Roberts & Rots 1973). |
Deviations from circular symmetry often present perplexing problems of interpretation where time-dependent effects must be taken into account. Fortunately, over the main optically bright parts of the disks of most spiral galaxies, these variations and differences are small enough to be treated as perturbations on a uniform circular rotation; however, they do compromise the goal of obtaining reliable mass distributions at large radial distances.